Биткоин и технологии криптовалюты
Хеш-указатели и структуры данных
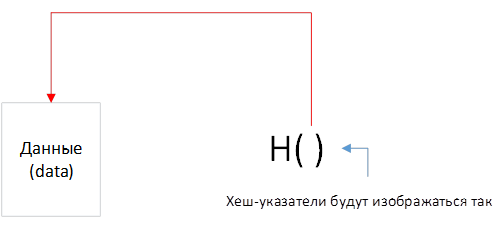
Хеш-указатель ( рис. 1.5) – это указатель на место хранения информации и (криптографический ) хэш этой информации
- запросить информацию, на которую он указывает обратно
- верифицировать то, что хэш не изменился, как следствие, не изменилась информация.
Таким образом, стандартный указатель предоставляет собой способ извлечения информации. А также дает возможность проверить, изменилась информация или нет. Следовательно, хэш-указатель показывает, где что-то расположено и каково его значение.
На рис. 1.5 показано, как в лекциях будет изображаться хэш-указатель. H( ) – хэш информации и стрелка, указывающая на эту информацию.
Использовать хэш-указатели можно для построения всех видов структур данных. Ключевая идея состоит в том, чтобы взять любую структуру данных — связные списки, дерево двоичного поиска или что-то подобное, — и реализовать его с помощью хэш-указателей вместо обычных указателей.
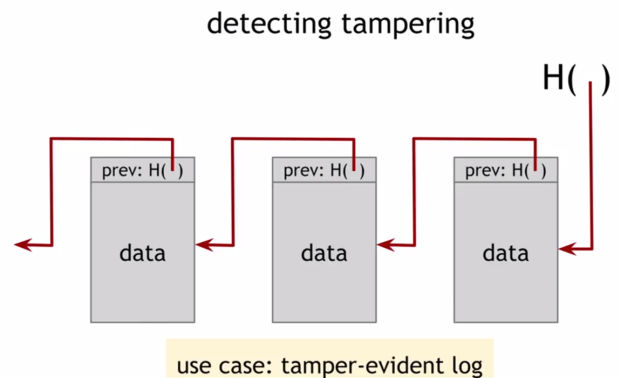
Для примера рассмотрим связный список, построенный с хэш-указателями( рис. 1.6). Эта структура данных называется цепочкой блоков (блокчейн).
Структура, похожая на обычный связанный список, в котором есть серия блоков и каждый блок содержит данные и указатель на предыдущий блок в списке. Здесь же предыдущий указатель блока будет заменен на хэш-указатель. Таким образом, он показывает, где он расположен и какое значение было у всего предыдущего блока. Начало списка сохраняется как обычный хэш-указатель.
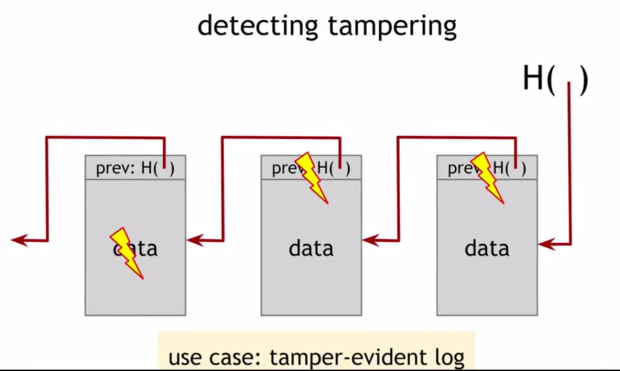
Примером использования подобной цепочки блоков является журнал контроля изменений. Создается журнал из структуры данных, в котором хранится большое их количество. Данные добавляются в конец журнала. Если кто-то решит подделать данные в журнале, это можно обнаружить, то есть осуществить контроль изменений. И чтобы понять, почему цепочка блоков имеет такое свойство, необходимо задаться вопросом, что произойдет, если злоумышленник захочет подделать данные, находящиеся в середине цепочки.
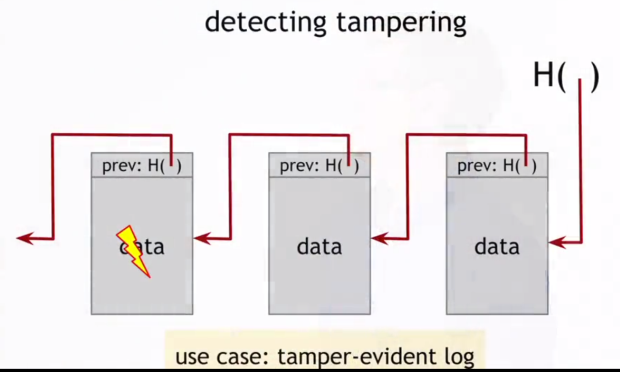
Предположим, злоумышленник хочет изменить блок данных ( рис. 1.7) так, чтобы владельцы хэш-указателя в заголовке не смогли обнаружить вмешательство.
Злоумышленник изменил содержимое блока, как показано на рис. 1.7. Изменится хэш всего этого блока и не будет совпадать с сохраненным ранее. И так как хэш-функция обладает свойством стойкости к коллизиям, то значение хэша этого блока будет отличаться, то есть изменения будут обнаружены
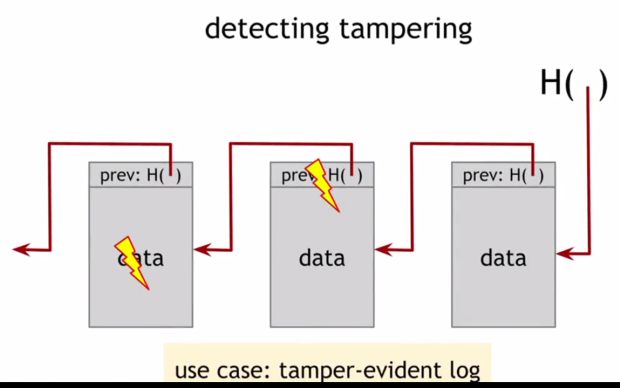
Если, конечно, значение хэш-указателя было рассчитано прежде, чем злоумышленник успел изменить хэш-указатель как показано на рис. 1.8. Если он изменяет этот хэш-указатель, то он может сделать так, чтобы он соответствовал данным в блоке. Но теперь он изменил содержание этого блока. А это значит, если содержимое этого блока будет позже хэшировано, то значение хэша не будет соответствовать хэшу, который был сохранен ранее, поскольку содержимое блока изменилось. Несогласованность между содержимым этого блока и хэшем будет обнаружена.
Если, конечно, злоумышленник также не подделает блок справа как показано на рис. 1.9. Но если он это делает, хэш этого блока не будет соответствовать хэшу, показанному как крайнее правое значение H(). А это значение злоумышленник не может изменить, потому что сохраненное значение является заголовком всего списка. И если злоумышленник хочет подделать данные в какой-либо точке данной цепочки, то, чтобы сохранить согласованность, ему придется изменять хэш-указатели вплоть до начала. В итоге он столкнется с серьезной проблемой, потому что не сможет подделать заголовок списка. Все это означает, что сохранение данного хэш-указателя является средством контроля изменений всего списка от начала до конца. Поэтому можно построить цепочку блоков похожую на эту, содержащую столько угодно блоков, но в начале имеющую особый блок, который можно назвать генезис-блоком. Все это представляет собой журнал контроля изменений, построенный из последовательности блоков.
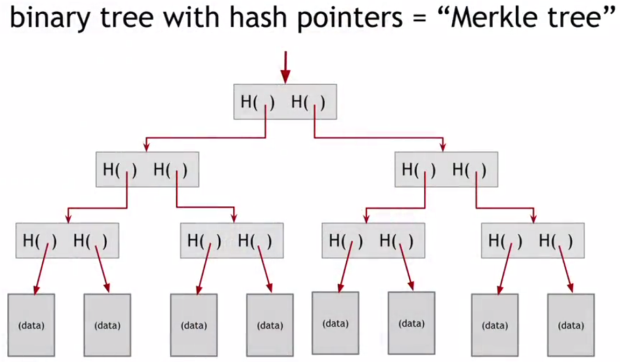
Следующей полезной структурой данных, которую можно построить с помощью хэш-указателей, является двоичное дерево. Такое дерево называется деревом Меркла, в честь Ральфа Меркла, который его изобрел.
Есть ряд блоков данных, которые располагаются внизу дерева ( рис. 1.10). Для каждой последовательной пары этих блоков строится структура данных, которая имеет два хэш-указателя, по одному для каждого из этих блоков. На уровне выше каждый блок будет содержать хэш-указатель этих двух дочерних элементов. И так далее, вплоть до корня дерева. И здесь в начале дерева, как и в предыдущем примере, сохраняется только хэш-указатель. По хэш-указателям можно перейти к любой точке списка. И можно убедиться, что данные не были изменены. Подобно ранее рассмотренной цепочке блоков, если злоумышленник исказит какой-то блок с данными внизу, это приведет к тому, что хэш-указатель на уровне выше будет другим. Поэтому он должен будет изменить и его. Затем ему придется изменить хэш-указатель, находящийся на уровень выше. И в конце концов он дойдет до вершины, где он не сможет изменить сохраненный хэш-указатель. Таким образом, любая попытка изменить любую часть данных внизу будет вскоре замечена только благодаря сохраненному хэш-указателю наверху.
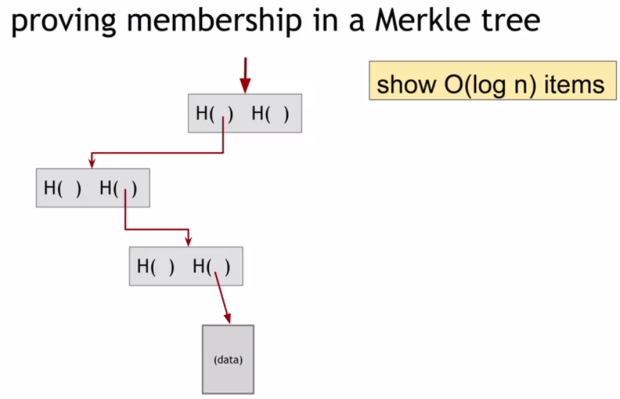
Еще одна приятная особенность деревьев Меркла заключается в том, что в отличие от ранее созданной цепочки блоков, если кто-то хочет доказать, что конкретный блок данных является членом этого дерева Меркла, все, что им нужно, это предоставить данные, представленные на рис. 1.11.
Поэтому, если сохранен только корень, и кто-то хочет доказать, что блок находится в дереве Меркла, он должен показать блок с рисунка рис. 1.11. Можно пройти по всему до блока данных, проверяя на соответствие сохраненные хэши. И только проверив хэши до корня, можно убедиться, что этот блок данных находится в дереве Меркла. Таким образом, если будет O(log n) элементов, которые нужно отобразить, то требуется O(log n) времени, чтобы их проверить. И поэтому даже при очень большом числе блоков данных в дереве Меркла, можно проверить достоверность их принадлежности за относительно короткое время.
Преимущества дерева Меркла:
В дереве содержится множество элементов, но помнить необходимо только хэш корня.
Можно проверить вхождение за О(log n) время/пространство
Разновидность: сортированное дерево Меркла
Можно проверить на вхождение за O(log n) (показать элементы перед, после пропавшего)
Таким образом, деревья Меркла имеют различные преимущества. Одно из них состоит в том, что дерево содержит много элементов, но нужно помнить только корневой хэш, который составляет всего лишь 256 бит. Можно проверить принадлежность к дереву Меркла в логарифмическом времени и логарифмическом пространстве. Есть разновидность дерева Меркла — сортированное дерево Меркла. Это то же самое дерево, но здесь блоки, расположенные внизу, сортируются в определённом порядке. Скажем, алфавитном, лексикографическом или числовом, или каком-либо другом. Как только дерево отсортировано, можно проверить достоверность данных в нем. То есть можно доказать, что конкретный блок не находится в дереве Меркла. Для этого нужно указать путь к элементу, который находится непосредственно перед тем, где будет этот элемент, и сразу после того места, где он должен быть. И тогда можно сказать, что оба эти элемента находятся в дереве Меркла, они последовательны. И поэтому между ними нет места. Между ними нет ничего, поэтому не может быть доказательства, что они не являются членами дерева. Итак, дерево Меркла — это дерево двоичного поиска, построенное с помощью хэш-указателей, в котором можно осуществить проверку членства логарифмическим временем, либо сортировкой, и это очень эффективно.
В более общем плане, получается, что можно использовать хэш-указатели в любой структуре данных, основанной на указателях, пока структура данных не имеет циклов. Если в структуре данных есть циклы, невозможно сделать все хэши соответствующими последовательности. Если представить ациклическую структуру данных, то в ней можно начать с любого элемента, у которого нет выходящих из него указателей, вычислять хэши этих объектов, а затем вернуться назад, в начало. Но в структуре с циклами нет конца, с которого можно начать и вычислить в обратную сторону к началу. Так например принадлежность к ориентированному ациклическому графу, состоящему из хэш-указателей, можно проверить довольно эффективно.
Это хорошо известный способ, который постоянно встречается во всех распределенных структурах данных и во всех алгоритмах, о которых будет рассказано в этом курсе.
Терминологический словарь
Структура данных — программная единица, позволяющая хранить и обрабатывать множество однотипных и/или логически связанных данных в вычислительной технике.
Связные списки — базовая динамическая структура данных в информатике, состоящая из узлов, каждый из которых содержит как собственно данные, так и одну или две ссылки ("связки") на следующий и/или предыдущий узел списка.
Двоичное (бинарное) дерево — иерархическая структура данных, в которой каждый узел имеет не более двух потомков (детей). Как правило, первый называется родительским узлом, а дети называются левым и правым наследниками.
Дерево Меркла — тип хэш-функции. Используется для того, чтобы проверять целостность данных (файлов), получить уникальный идентификатор файла, а также дает возможность восстановить файл.