Альтернативы Proof of Work
В этой лекции будут рассмотрены альтернативы принятому в биткоине алгоритму защиты - доказательству выполненной работы (вычислительная задача proof of work, которая далее для краткости будет называться алгоритм, вычислительная задача или просто задача). Вычислительные задачи являются главной основой биткоина, потому что именно они применяются в системе поощрений. Майнеры получают вознаграждения за решение задач. Логично сделать предположение, что майнеры будут использовать любую возможность для ускорения нахождения правильного решения. И напротив, если существует свойство, помогающее экосистеме, но не способствующее непосредственному решению задач, оно не будет задействовано. Поэтому алгоритм вычислений играет очень важную роль в регулировании и направлении развития вычислительной сети.
Рассмотрим основные характеристики вычислительной задачи, основанной на криптографическом алгоритме SHA-2, которая в настоящее время используется в биткоин. Так, например, очень трудно найти полный набор решений для вычислительной задачи, что делает стоимость вычислительной мощности сети биткоина очень высокой или, другими словами, успешное решение задачи (нахождение блока) маловероятным. С другой стороны, скорость нахождения решений поддерживается на приемлемом уровне (около десяти минут). Это стимулирует майнеров, не имеющих больших вычислительных мощностей, участвовать в сети и позволяет им компенсировать затраты на ресурсы.
Если разрабатывать новый алгоритм вычислительных задач, какие особенности позволят ему завоевать популярность? Что будет помогать правильному развитию сети и препятствовать неверному?
В этой лекции будет рассказано о множестве альтернативных вариантов вычислительных задач. Некоторые из них уже используются на практике в криптовалютах, существующих сегодня. Другие являются лишь исследовательскими идеями, которые могут найти применение в будущем. Задачи преследуют множество возможных целей, например, сопротивление ASIC'ам, которое позволит выровнять условия для пользователей, имеющих специальное вычислительное оборудование и не имеющих такового. В лекции будут исследованы свойства, которые препятствуют объединению майнеров в пулы, и алгоритмы доказательства работы, которые имеют определенную социальную пользу. Будут также рассмотрены требования к защите, поскольку любые интересные дополнительные функции бесполезны, если не выполнены базовые требования к безопасности биткоина.
Общие требования к алгоритмам PoW.
Перед тем как приступить к рассмотрению альтернативных алгоритмов, нужно понимать основные требования, необходимые для жизнеспособности любого из вариантов.
Существует множество условий, которые должны быть выполнены. Так, например, решения должны быть легко верифицируемыми, потому что каждый узел в сети, даже не участвующий в активном майнинге, проверяет решение задачи. Уровень сложности задач должен быть изменяемым. Так, чтобы трудность нахождения решения могла изменяться со временем, поскольку новые майнеры при подключении к сети увеличивают ее вычислительную мощность.
Обсудим детально одно из основных, но неочевидных, требований. Вероятность нахождения удачного решения для задачи в любой момент времени должна быть пропорциональна используемой майнером вычислительной мощности. На практике это означает, что даже у слабых участников сети должен быть некоторый, пропорциональный их вычислительной мощности, шанс найти блок и получить вознаграждение за это. Для иллюстрации этого требования рассмотрим пример плохого алгоритма, который не удовлетворяет этому требованию. Представьте вычислительную задачу, которая требует N шагов для решения, и именно ее результат учитывается для получения вознаграждения.
Проблема такой постановки задачи в том, что каждый раз вознаграждение получит самый быстрый майнер сети. Предположим, что есть два майнера с одинаковой скоростью работы и третий, превосходящий их по скорости в 2 раза. Тогда быстрейший найдет решение, пока другие будут лишь на половине пути. Третий майнер будет получать все вознаграждения, для остальных же мотивация в участии пропадает.
Правильный алгоритм дает каждому шанс на победу, в зависимости от используемой им вычислительной мощности. Если майнеры из предыдущего примера будут бросать дротики в мишень, пропорциональную имеющимся у них вычислительным мощностям, каждый может попасть в цель. Но у третьего майнера вероятность попадания будет выше, так как его мишень будет больше. Алгоритмы такого типа называют не прогрессирующими.
Это был пример одного из необходимых условий, остальные будут рассмотрены в ходе рассказа про альтернативные типы вычислительных задач.
Алгоритмы с защитой от ASIC
Рассмотрим алгоритмы, устойчивые к использованию ASIC. Этот вид вычислительных задач в настоящее время является наиболее обсуждаемым. Тому есть несколько причин. В начале биткоины добывали, используя обычные ПК, позже для майнинга появились специальные интегральные схемы, сегодня почти весь майнинг идет на ASIC и использование ПК не окупает себя. Но это плохо для экосистемы, поскольку сейчас барьер для входа очень велик, а раньше новые пользователи активно включались в сеть. Для майнинга было достаточно оставить ПК включенным на ночь. Чтобы решить данную проблему, нужно придумать алгоритм, который свел бы к минимуму разницу между обычным ПК и специализированным оборудованием. Дополнительно можно выделить еще одну цель – снизить влияние производителей ASIC на сеть. Это важно, поскольку сейчас существует всего несколько крупных игроков на этом рынке. И они могут консолидировать в своих руках очень большую вычислительную мощность. У пользователей есть подозрения, что производители специально задерживают отправку ASIC устройств, добывая биткоины фактически за деньги покупателей. Еще одна возможная угроза – появление новой прорывной технологии для создания подобных устройств, которую производитель оставит в тайне и получит доминирующее положение в сети.
Наиболее популярный пример алгоритмов, устойчивых к ASIC, требует значительного объема памяти. Предпосылка довольно проста – в соответствии с законом Мура (см. Закон Мура) каждые 2 года количество транзисторов на кристалле ЦПУ должно удваиваться. Память и системы хранения данных так же развиваются, но скорость их развития намного ниже. И разрыв лишь увеличивается со временем. Из вышесказанного следует, что, если использовать алгоритм, требующий много памяти вместо просто вычислительной мощности, разница в производительности между специальным оборудованием и ПК будет меньше.
Самый известный алгоритм такого типа – scrypt. Вычисление SHA-256, используемого в биткоине, требует всего лишь 256 бит памяти. Такой объем легко разместить в регистрах процессора. Время на каждую операцию составляет порядка сотен миллисекунд. Значит, для полного перебора вариантов достаточно использовать много параллельных устройств. Scrypt же использует достаточно большое (по меркам однокристальных интегральных схем) количество памяти для хранения большого массива псевдослучайных чисел, которые генерируются на первом шаге алгоритма. Данные массива запрашиваются в случайном порядке и комбинируются с друг другом для создания ключа. Поскольку алгоритм генерации массива известен, то можно реализовать scrypt без использования памяти, но это потребует пересчета части элементов массива каждый раз заново, что достаточно сложно и занимает много времени. Таким образом, scrypt вносит баланс между количеством затрачиваемой памяти и временем.
Scrypt применяется во второй по популярности криптовалюте – Лайткоин (Litecoin). Кроме того, этот алгоритм используется для криптозащиты паролей, которая так же имеет целью защиту от ASIC. Это дает дополнительную уверенность в безопасности криптовалюты.
Рассмотрим шаги вычислений подробнее.
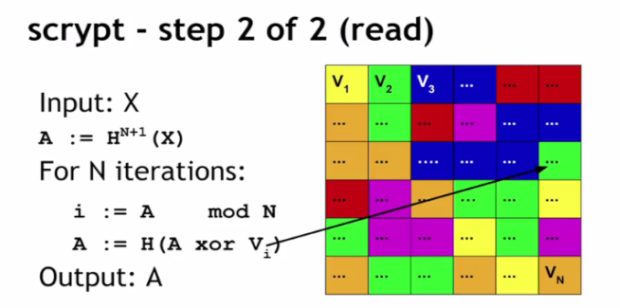
Пусть на входе строка символов Х. На первом шаге n ячеек памяти (n-количество шагов алгоритма) заполняются таким образом: в первую ячейку записывается V1 хэш от X, во вторую V2 хэш от первой ячейки, в третью V3– хэш от значения второй ячейки и так далее ( рис. 8.1).
На втором шаге происходит чтение случайно выбранных данных из памяти.
Сначала рассчитывается значение-аккумулятор А, равное хэшу от последней ячейки. В цикле из n шагов с использованием текущего значения A высчитывается индекс ячейки i, из которой будут читаться данные. i находится как остаток от деления A на n. А на каждом шаге высчитывается как сложение по модулю 2 (XOR) А и Vi. После n шагов получаем итоговое A, которое и будет значением функции.
Если реализовывать алгоритм без буфера памяти, для вычисления A надо было каждый раз пересчитывать Vi . Общее количество пересчетов равно сумме арифметической прогрессии от 1 до n, то есть приблизительно n/2. Полное количество вычислений SHA-256 получится n*n/2=n2/2 против 2n вычислений в случае использования буфера. То есть быстрее в n/4 раз.
На практике у scrypt есть несколько минусов. Первый – проверка решения так же требует памяти и цикла в n шагов. Поэтому при применении алгоритма в качестве доказательства работы накладывается ограничение на величину n, как в плане выделения памяти, так и в плане времени выполнения.
Так же вызывает сомнения, насколько он защищен от ASIC. Дело в том, что для выбранных в Litecoin параметров сложности (N) недостаточно для сглаживания разницы между ASIC и ПК. На рынке уже появились специальные устройства для майнинга, однако, стоит заметить, что их производительность в миллионы раз ниже, чем для биткоинов.
Зато у scrypt есть один неоспоримый плюс – поскольку эта функция используется так же для шифрования паролей, то по мере ее совершенствования возможно желаемый эффект будет достигнут.
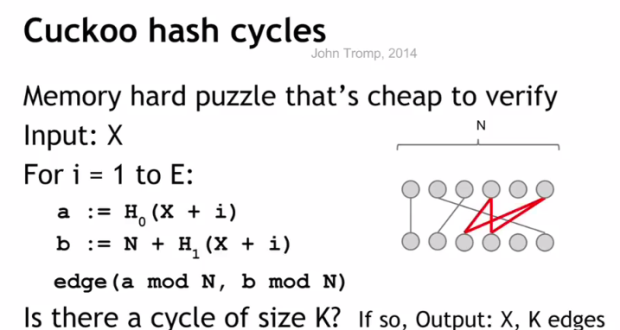
Рассмотрим другой пример алгоритма требующего использования памяти для работы. Он называется кукушкино хэширование. Для поиска решения на основании строки X строится неориентированный граф. Вершины графа выбираются по алгоритму
for i = 1 to n: i = X % N a = H0(X +i) b=N+ H1(X+1)
Ребра графа строятся так:
Теперь необходимо определить, есть ли в данном графе цикл длинной K (входной параметр функции). Если такой цикл найден, то ответом будет Х и индексы вершин.
Почему данный алгоритм требует много памяти? Дело в том, что нахождение циклов в графе хорошо изучено, но используемые для этого методы требовательны к объему ОЗУ. Зато проверить решение проще, чем в scrypt, нужно просто пересчитать вершины найденного цикла. И для этого не нужно много ресурсов.
Существуют и другие подходы к проблеме защиты от ASIC:
- алгоритм x11 – последовательное взятие 11 разных хэш функций. Создание ASIC для каждой функции отдельно возможно, однако, их объединение резко увеличивает стоимость и затрудняет построение эффективного устройства.
- постоянное изменение вычислительной задачи. При таком подходе каждый промежуток времени нужно будет создавать новый ASIC. Но при этом также возникнут проблемы у обычных майнеров – потребуется одновременное обновление всей сети. Кроме того, если новый алгоритм недостаточно надежен, возрастает вероятность возникновения коллизий.
- наконец есть те, кто предлагает не защищаться от ASIC. Да, сейчас для биткоина используются устройства, великолепно считающие SHA-2. Это уже давно известная технология и резкий эволюционный скачок ее развития маловероятен. Как уже говорилось ранее, большие ASIC это всего лишь объединения множества маленьких ASIC. Значит, стоимость устройств растет параллельно с их производительностью.