Биткоин и технологии криптовалюты

Криптографические хэш-функции

Прежде чем говорить о биткоинах, необходимо разобраться с понятием хэш-функция (или, другое название, функция свертки). В этой лекции будет рассмотрено, что такое хэш-функция, каковы ее основные свойства и как ее можно применять на практике.

Криптографическая хэш-функция является математической функцией. Она характеризуется тремя свойствами. Прежде всего, хэш-функция может принимать на вход строку любого размера. На выходе будет значение фиксированного размера. В лекциях будет рассмотрено использование 256-битного ключа, потому что именно он используется в биткоине. Третье свойство - ключ должен быть эффективно вычисляем. Это значит, что если дана произвольная строка, то за определенный промежуток времени можно получить результат вычисления хэш-функции.

В данной лекции также будут рассмотрены три основные криптографические свойства хэш-функции, делающие ее защищенной: устойчивость к коллизиям, свойство скрытия (необратимость) и открытость к вычислению.

Хеш-функция:

• на вход получает любую строку
• на выходе выдает строку фиксированного размера (в этом курсе длина строки 256 бит)
• эффективно вычисляема

Криптографические свойства хэш-функции:

• устойчивость к коллизиям
• необратимость
• открытость к вычислению

Рис. 1.1. Стойкость к коллизиям

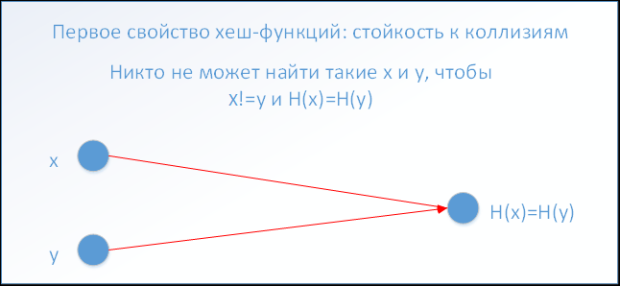
1-е свойство хэш-функций: стойкость к коллизиям ( рис. 1.1).

Никто не может найти такие x и y, чтобы

х!= y и H(x)=H(y).

То есть невозможно подобрать различные значения x и y, для которых значения хэш-функции совпадают.

Хеш-функцию также называют функцией свертки, а значение функции для конкретного x – сверткой.

На рис. 1.1 красные стрелки показывают значение x и его свертку — H(x), и y с сверткой H(y). Обратите внимание, что на рисунке сказано:"Никто не может найти". Но этот не значит, что коллизии не существуют. Коллизии существуют, и чтобы понять почему, необходимо обратиться к рис. 1.2.

Рис. 1.2. Коллизии существуют

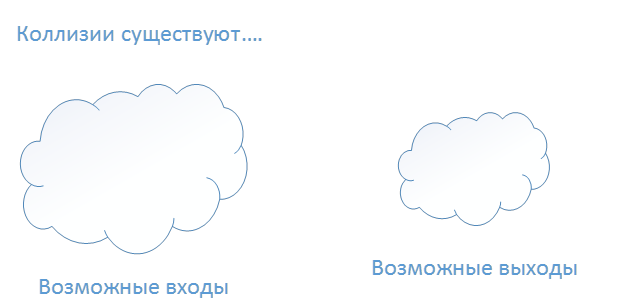
Слева на рис. 1.2 изображены все возможные значения на входе хэш-функции. Значение может быть строкой любого размера. А справа — все возможные результаты, которые должны быть размером 256 бит. Итак, справа - результаты, и их всего 2²⁵⁶ возможных значений. Слева же значений больше. Вопрос в том, сможет ли кто-либо обнаружить коллизию ( рис. 1.3).

Рис. 1.3. Можно ли найти коллизию?

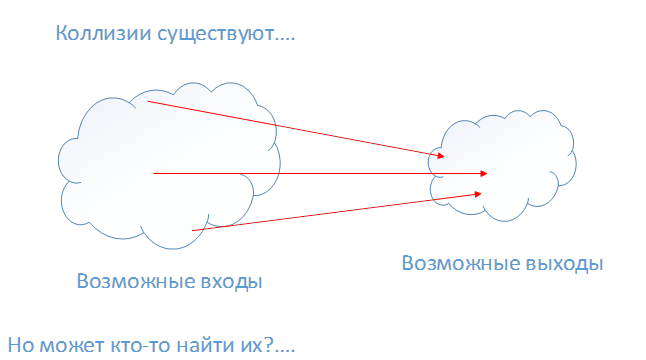
Определенная точка слева всегда соответствует определенной точке справа. Значения справа сжимаются (сворачиваются). В действительности должны быть значения слева, которые будут указывать на одно и то же значение справа. Такие значения называют коллизиями.

То есть коллизии существуют, и ключевой вопрос в том, можно ли их найти?

При этом есть гарантированно работающий метод поиска коллизии:

Нужно взять 2¹³⁰ случайных значений на вход (левое облако на рис. 1.3). Проверив все эти 2¹³⁰ значения, можно сказать, что есть вероятность, равная 99,8%, что, по крайней мере, два из них будут образовывать коллизию.

Таков простой метод поиска коллизий. Он работает независимо от того, какова хэш-функция. Но проблема состоит в том, что процесс занимает очень много времени. Необходимо вычислить хэш-функцию 2¹³⁰ раз. И это, несомненно, огромное число.

Для того чтобы понять сколько это займет времени, можно представить, что если каждый компьютер, когда-либо созданный человеком, вычислял коллизии с самого начала появления Вселенной и до наших дней, то вероятность того, что коллизия будет обнаружена все еще бесконечно мала. Настолько мала, что значительно меньше, чем вероятность того, что Земля будет уничтожена гигантским метеором в течение следующих двух секунд.

Рассмотренный метод занимает слишком много времени, чтобы принимать его во внимание. Вопрос в том, есть ли какой-нибудь другой метод, который можно было бы использовать для конкретной хэш-функции, чтобы найти коллизию? Есть ли более быстрый способ поиска коллизий? На этот вопрос сложнее ответить.

Для некоторых хэш-функций, конечно, есть. Например, если хэш-функция принимает на вход любое число, а на выходе выдает число по модулю 2²⁵⁶, то есть оставляет последние 256 бит значения. Тогда можно легко найти коллизию. Одной из коллизий будет значение 3 и 3 плюс 2²⁵⁶. Таким образом, для некоторых возможных хэш-функций очень легко найти коллизию, для других - нет.

Следует также отметить, что нет такой хэш-функции, для которой доказано, что у нее нет коллизий. Есть только некоторые функции, для которых пытались найти коллизии, но так и не смогли. И поэтому решили, что они не имеют коллизий.

Какая польза от использования хэш-функций? Например, устойчивую к коллизиям хэш-функцию можно использовать в качестве краткого содержания, то есть как своего рода профиля сообщения. Если мы видим, что значения хэша одинаковые, то предполагаем, что одинаковыми были и изначальные значения. Потому что, если бы кто-то знал, что x и y, имеющие один хэш-код, — разные, то это, конечно же, была бы коллизия. А поскольку это неизвестная коллизия, тогда, зная, что значения хэша одинаковы, можно предположить, что значения на входе одинаковы. Это позволяет использовать хэш в качестве краткого содержания передаваемого сообщения.

Предположим, есть большой файл. И нужно иметь возможность проверить позже, является ли другой файл тем же файлом, который был изначально, не были ли внесены изменения. Можно сохранить у себя копию, и при необходимости сравнить ее с оригиналом. Но можно поступить проще и эффективнее - просто запомнить хэш исходного файла. Затем, если кто-то показывает новый файл и утверждает, что это тот же самый, можно вычислить хэш этого нового файла и сравнить с имеющимся. Если значения хэш одинаковы, можно сделать вывод, что файлы одинаковые.

Это очень эффективный способ запомнить то, что было раньше, и проверить достоверность позже. И это, безусловно, полезно, потому что размер значения хэш небольшой — всего лишь 256 бит. Исходный файл может быть очень большим.

Второе свойство хэш-функций состоит в том, что они необратимы. Это свойство можно описать следующим образом. Если известен результат хэш-функции, то нет никакого способа определить, какое значение x было на входе. Проблема в том, что это свойство не всегда выполняется точно. И чтобы понять, почему это так, рассмотрим пример.

Допустим, кто-то подбрасывает монетку. И если выпадает "орел", то на выходе возвращается хэш строки "орел". А если — "решка", то — хэш строки "решка".

Человек, который не видел, как подбрасывают монетку, а видел только хэш на выходе, легко может узнать, какая строка была хэширована. Ему необходимо будет вычислить два хэша (для "орла" и "решки"), сравнить их с хэшем на выходе и сразу станет понятно, каков был результат подбрасывания монетки.

Если хэш-функция необратима, то не должно быть случая, когда значение х можно легко вычислить, зная H(x). То есть, х должен выбираться из ряда, который до некоторой степени не определён и широк. Так что попытка подобрать возможные значения х или выбрать из нескольких похожих значений не сработает.

Свойство необратимости, которое рассматривается в этой лекции, немного сложнее. И вот способ, с помощью которого можно исправить проблемы с простым значением х, таким как в примере с подбрасыванием монетки ("орел" и "решка"). Необходимо взять значение х и объединить его со значением r, которое выбрано случайным образом.

Если r выбрано из распределения вероятностей с высокой min-энтропией, то для данного H(r|x), невозможно найти x.

Высокая min-энтропия (см. энтропия Реньи) означает, что распределение настолько широкое, что ни одно значение не может быть выбрано с какой-либо более-менее определенной вероятностью.

H (r|x) означает, что берутся все биты значения r и за ними помещаются все биты значения x. То есть, если берется хэш значения r с хэшем значения х, из этого объединения невозможно вернуть х. И это будет истинно для формально определенного свойства, что если r — случайное значение, выбранное из распределения вероятностей с высокой min-энтропией, то для данного H (r|x), невозможно найти x. Что значит высокая min-энтропия? Это можно описать так, что r выбирается случайно из огромного количества различных значений. Так, например, если r выбирается равномерно из всех строк длиной 256 бит, то любая конкретная строка выбиралась с вероятностью 1 из 2²⁵⁶, то есть 2^-256, а это действительно очень малое число. Итак, до тех пор, пока r выбирается таким образом, хэш r, объединенный с x, будет скрывать x.

Теперь давайте рассмотрим применение этого свойства – обязательство (commitment). Это своего рода цифровая аналогия, когда берется значение и запечатывается в конверте. Конверт кладется на стол, где всякий может его увидеть. То есть фиксируется то, что находится в конверте.

Конверт остается закрытым, и его значение никому не известно. Позже его можно открыть и извлечь содержимое, но до этого оно запечатано.

В криптографии схема обязательства является методом, позволяющим пользователю подтверждать какое-либо значение, которое не разглашается (аналогия - запечатанный конверт). В случае разглашения этого значения (вскрытия конверта) благодаря обязательству будет известно, что пользователь знал содержимое конверта на момент создания обязательства и с этого момента оно не изменилось.

Чтобы создать обязательство, используются секретный ключ(key) и сообщение (msg). Данный процесс вернет два значения - обязательство (com) и ключ (key).

Если проводить аналогию с конвертом, обязательство – это запечатанный конверт, лежащий на столе. Ключ нужен для того, чтобы вскрыть конверт и проверить его содержимое на отсутствие изменений.

Чтобы в определенный момент позволить проверить содержимое конверта, необходимо предоставить ключ, которым он был запечатан, и исходное сообщение. Используя обязательство, ключ и сообщение любой может распечатать конверт и проверить, изменилось ли его содержимое.

Свойства безопасности обязательства:

1 свойство - необратимость: для данного com, невозможно найти msg.

2 свойство - невозможно найти msg1!= msg2 такое, чтобы verify(commit(msg1), msg2) == true

Первое свойство дает возможность опубликовать обязательство (положить запечатанный конверт на стол). Обязательство можно будет увидеть, но по нему нельзя восстановить исходное сообщение (нельзя распечатать конверт, имея только обязательство).

Второе свойство доказывает неизменность сообщения в конверте. То есть, невозможно найти два разных сообщения, чтобы создать обязательство одного сообщения, а позже сказать, что передали другое, и все это будет верифицировано.

Откуда известно, что эти два свойства неизменны? Для начала нужно рассмотреть, как можно их использовать.

Чтобы создать обязательство сообщения, генерируется случайное 256-битное значение - ключ. В качестве обязательства возвращается хэш конкатенации ключа и сообщения (H(key|msg)). В качестве значения ключа используется хэш этого ключа. Чтобы сделать проверку, нужно вычислить хэш ключа, объединенного с сообщением.

Перейдем к свойствам безопасности.

для данного H(key|msg), невозможно найти msg.

То есть для данного обязательства (com= H(key|msg)) невозможно найти сообщение (msg).

Это свойство необратимости, которое было рассмотрено ранее. Ключ — это случайное 256-битное значение. Свойство необратимости гласит, что если будет взято сообщение, и перед ним поставлено значение, которое было выбрано случайным образом и размером 256 бит, тогда невозможно найти значение сообщения.

Следующее свойство – стойкость к коллизиям. Невозможно найти два разных сообщения, с одинаковым хэшем.

Обязательство: невозможно найти msg1 != msg2 такое, чтобы

(H(key | msg1) == (H(key | msg2)

Схема обязательств будет работать только благодаря двум рассмотренным свойствам безопасности.

3-е свойство хэш-функций - открытость для сложного вычисления.

Для любого возможного значения на выходе y, если k берется из распределения с высокой min энтропией, невозможно найти такой x, чтобы H(k | x) = y.

Для любого возможного значения на выходе — y, которое можно получить из хэш-функции, если k выбрано случайным образом из распределения с высокой min-энтропией, нет возможности найти x, так чтобы хэш конкатенации k и x был равен y.

Это исключает возможность того, что кто-то из хэш-функции получит определенное выходное значение y. Если взять в качестве ввода значение, выбранное в удобном рандомизированном виде, то очень сложно найти другое значение, которое попадает именно в эту цель.

Чтобы понять, как это можно использовать, рассмотрим сложную поисковую задачу. Сложность задачи заключается в том, что решение можно найти только обойдя очень большое пространство и нет других путей решения, кроме перебора этого пространства.

Применение: сложная поисковая задача

При заданном идентификаторе задачи (puzzle ID) id (из распределенной последовательности с высокой min-этропией) и целевым значением Y:

Пытаться найти решение x, такое чтобы

H(id | x) ∈ Y

Свойство открытости для сложного вычисления подразумевает, что нет лучшей стратегии решения, чем попытка случайного поиска значения x.

Идея состоит в том, имеется идентификатор задачи (id), который выбирается из некоторой высокой распределенной случайной последовательности с высокой min-энтропией. И задана цель — Y, которая должна быть равна хэш-функции. Необходимо попытаться найти решение - x. Таким образом, если хэшировать идентификатор задачи (ID) вместе с решением X, будет получен результат, который находится в заданном Y. Y — это целевой диапазон или набор желаемых результатов хэширования. ID определяет конкретную задачу, а x — ее решение.

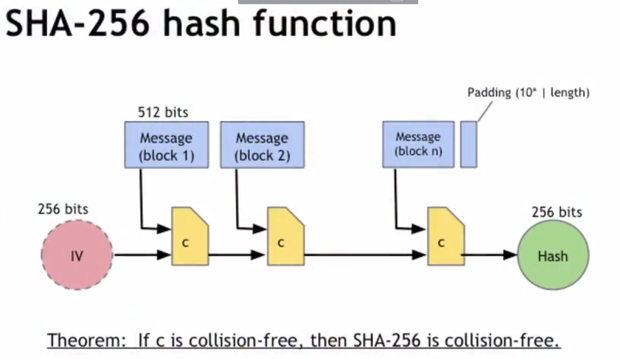
Свойство открытости для сложного вычисления подразумевает, что для этой задачи не существует лучшей стратегии решения, чем простой подбор случайных значений x. И поэтому, если нужно сформулировать сложную задачу, необходимо генерировать идентификаторы задачи (ID) в подходящем случайном порядке. Эта вычислительная задача будет рассмотрена в следующих лекциях в контексте биткоин майнинга. Обратимся к хэш-функции, которую использует биткоин рис. 1.4.

Рис. 1.4. Стойкость к коллизиям

Она называется SHA-256 и работает следующим образом. Берется сообщение, которое необходимо хэшировать, и разбивается на блоки размером 512 бит (синие блоки на рис. 1.4). Сообщение не должно быть кратно размеру блока, поэтому в конце будет добавляться дополнение (padding ). В конце дополнения будет поле длиной 64 бит, которое обозначает длину сообщения в битах. А перед дополнением будет стоять один бит, за которым следует некоторое количество нулевых бит, чтобы заполнить блок до конца. Когда длина сообщения станет кратной блоку размером 512 бит, оно разбивается на эти блоки. Потом выполняется вычисление. Оно начинается с 256-битного значения, называемого IV. Это номер, который можно просмотреть в стандартном документе. Берется IV и первый блок сообщения, получается 768 бит, и пропускается через функцию сжатия. На выходе получается 256 бит. То же самое делается со следующими 512 битами сообщения – этот цикл продолжается до конца. Каждая итерация сжимает последующий 512-битный блок сообщения и включает его в логический результат. Результатом вычисления станет хэш, размером 256 бит. При этом нет проблемы доказать, что если функция обладает свойством стойкости к коллизиям, то вся хэш-функция также будет обладать стойкостью к коллизиям. В этой части лекции были рассмотрены хэш-функции, их свойства и использование этих свойств. Описана хэш-функция, которая используется в биткоине. В следующем разделе лекции будут рассмотрены способы использования хэш-функций для создания более сложных структур данных, которые используются в распределенных системах, таких как биткоин.

Терминологический словарь

Бит – единица измерения информации в двоичной системе счисления.

Хеширование (англ. hashing) — преобразование массива входных данных произвольной длины в (выходную) битовую строку фиксированной длины, выполняемое определённым алгоритмом.

Хешем (хэш-суммой, хэш-кодом) называется результат обработки неких данных хэш-функцией.

Хеш-функция – алгоритм, конвертирующий строку произвольной длины (сообщение) в битовую строку фиксированной длины, называемую хэшем, хэш-кодом.

Криптография — наука о методах обеспечения конфиденциальности (невозможности прочтения информации посторонним), целостности данных (невозможности незаметного изменения информации), аутентификации (проверки подлинности авторства или иных свойств объекта), а также невозможности отказа от авторства.

Криптографическая хэш-функция — всякая хэш-функция, являющаяся криптостойкой, то есть удовлетворяющая ряду требований, специфичных для криптографических приложений.

Коллизия хэш-функции — это равенство значений хэш-функции на двух различных блоках данных.