|
В дисциплине "Основы эконометрики" тест 6 дается по теме 7. |
Сглаживание временных рядов
6.1. Линейные фильтры
Одним из распространенных способов выявления тренда является сглаживание временного ряда. Его суть сводится к замене фактических значений ряда расчетными, полученными после удаления высокочастотных колебаний. Поэтому сглаживание ряда часто называют фильтрованием, а преобразование ряда (оператор), с помощью которого осуществляется фильтрование, - фильтром.
Наиболее часто на практике используются линейные фильтры. Общая формула линейного фильтра такова
где
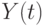 |
- | сглаженное (отфильтрованное) значение временного ряда в момент времени  ; ; |
 |
- | вес, приписываемый значению исходного ряда, находящемуся на расстоянии  от рассматриваемого момента времени от рассматриваемого момента времени  . . |
Фильтр (6.1) учитывает  значений (уровней) ряда после момента времени
значений (уровней) ряда после момента времени  и
и 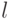 уровней до него. Число
уровней до него. Число 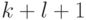 значений исходного ряда, одновременно участвующих в сглаживании, называется шириной интервала сглаживания. Если
значений исходного ряда, одновременно участвующих в сглаживании, называется шириной интервала сглаживания. Если 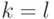 , то сглаживание центрированное. Сглаженный ряд короче исходного ряда на
, то сглаживание центрированное. Сглаженный ряд короче исходного ряда на  значение. В зависимости от выбора ширины интервала сглаживания, величины весов
значение. В зависимости от выбора ширины интервала сглаживания, величины весов  применяются различные методы сглаживания, самым простым из которых является метод простой скользящей средней.
применяются различные методы сглаживания, самым простым из которых является метод простой скользящей средней.
6.2. Метод простой скользящей средней
Если 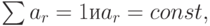 то фильтр (6.1) означает вычисление средней арифметической, которую называют скользящей средней.
то фильтр (6.1) означает вычисление средней арифметической, которую называют скользящей средней.
Для удобства сопоставления сглаженного и исходного рядов ширину интервала сглаживания чаще выбирают нечетным числом 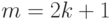 . Тогда
. Тогда 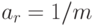 и из (6.1) получаем
и из (6.1) получаем
Такое сглаживание будет симметричным  и центрированным. Чаще всего для сглаживания берут
и центрированным. Чаще всего для сглаживания берут 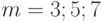 . Если дисперсия уровней исходного ряда постоянная и равна
. Если дисперсия уровней исходного ряда постоянная и равна 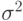 , а сами члены ряда
, а сами члены ряда  независимы между собой, то дисперсия сглаженного ряда
независимы между собой, то дисперсия сглаженного ряда 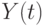 равна
равна 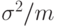 . Таким образом, при увеличении колеблемости исходного ряда
. Таким образом, при увеличении колеблемости исходного ряда 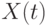 (при наличии большой дисперсии
(при наличии большой дисперсии 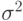 ) для уменьшения амплитуды колебаний у сглаженного ряда
) для уменьшения амплитуды колебаний у сглаженного ряда 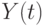 необходимо увеличивать ширину интервала сглаживания
необходимо увеличивать ширину интервала сглаживания  либо проводить процедуру сглаживания повторно. Кстати, по степени уменьшения дисперсии у повторно сглаженных рядов можно судить о степени зависимости между собой членов исходного ряда, т.е. о наличии "долговременной памяти" у исходного ряда.
либо проводить процедуру сглаживания повторно. Кстати, по степени уменьшения дисперсии у повторно сглаженных рядов можно судить о степени зависимости между собой членов исходного ряда, т.е. о наличии "долговременной памяти" у исходного ряда.
Если ряд имеет периодические колебания с продолжительностью цикла меньше  , то они полностью исчезают при сглаживании с помощью скользящей средней с шириной интервала сглаживания
, то они полностью исчезают при сглаживании с помощью скользящей средней с шириной интервала сглаживания  .
.
Расчет 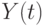 при
при  можно упростить, применяя рекуррентную формулу
можно упростить, применяя рекуррентную формулу
При расчетах по формуле (6.3) первое сглаженное значение  вычисляется по формуле (6.2)
вычисляется по формуле (6.2)

Недостатком метода простой скользящей средней является равное участие в сглаживании значений ряда, отстоящих от момента сглаживания  на разном расстоянии. В результате этого могут быть потеряны важные для анализа свойства ряда. Рассмотрим более "тонкие" методы сглаживания.
на разном расстоянии. В результате этого могут быть потеряны важные для анализа свойства ряда. Рассмотрим более "тонкие" методы сглаживания.