|
В дисциплине "Основы эконометрики" тест 6 дается по теме 7. |
Лабораторная работа № 1: Модель парной линейной регрессии
По имеющимся данным требуется:
- вычислить дескриптивные (описательные) статистики:
- выборочные средние,
- выборочную дисперсию,
- выборочное среднее квадратичное отклонение,
- нижний и верхний квартили выборочного распределения,
- размах выборки,
- - и 99%-ные доверительные интервалы для оценки математического ожидания (и дисперсии) исходя из того, что выборочные данные имеют нормальное распределение;
- вычислить выборочный коэффициент корреляции и оценить его значимость на 5%-ном уровне;
- построить корреляционное поле заданных переменных и сформулировать гипотезу о виде связи;
- вычислить параметры уравнения парной регрессионной модели;
- оценить значимость построенного уравнения регрессии с помощью
 -критерия;
-критерия; - оценить качество построенного уравнения регрессии с помощью коэффициента детерминации
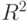 ;
; - построить 95%-ные интервалы для оценок параметров уравнения регрессии;
- рассчитать прогнозное значение, если значение независимой переменной увеличится на 10% от его среднего значения. Построить 95%-ный доверительный интервал для прогнозного значения;
- оценить с помощью коэффициента эластичности (среднего) силу связи независимой переменной с зависимой;
- рассчитать параметры уравнений регрессий других форм: степенной, логарифмической, экспоненциальной и др.
Отчет по лабораторной работе № 1
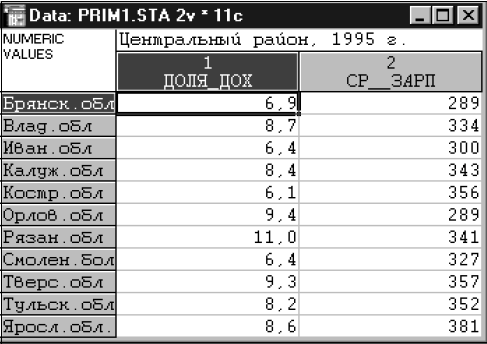
I. В работе были использованы приведенные данные (табл. 1) по территориям Центрального района РФ за 1995 г. по следующим показателям:
Таблица 1
- доля денежных доходов, направленных на прирост сбережений во вкладах, займах, сертификатах и на покупку валюты, в общей сумме среднедушевого денежного дохода (%) - Доля_дох;
- среднемесячная начисленная заработная плата (тыс. руб.) - Ср_зарп.
По каждой из переменных были вычислены дескриптивные статистики, представленные в табл. 2.
| Статистики | ПОТ_РАСХ | СР_ЗП |
| Выборочное среднее | 8,13 | 333,55 |
| Выборочная дисперсия | 2,35 | 892,87 |
| Выборочное среднее квадратичное отклонение | 1,53 | 29,88 |
| Нижний квартиль | 6,40 | 300,00 |
| Верхний квартиль | 9,30 | 356,00 |
| Размах выборки | 2,90 | 56,00 |
| 95%-ный доверительный интевал для М(Х) | (7,10; 9,16) | (313,47; 353,62) |
| 99%-ный доверительный интевал М(Х) | (6,67; 9,59) | (304,99; 362,09) |
| 95%-ый доверительный интевал для D(Х) | (1,15; 7,23) | (148,85; 938,43) |
Выборочный коэффициент корреляции равен 0,21, при этом значение 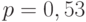 . Такая величина
. Такая величина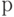 -уровня свидетельствует о том, что коэффициент корреляции не является статистически значимым. Другими словами, имеющиеся данные о среднемесячной заработной плате и доле сбережений населения не позволяют сделать вывод о наличии значимой связи. Выборочное значение коэффициента корреляции следует рассматривать как значение, случайно полученное при формировании выборки, т.е. отклонение от нулевого значения не отражает истинной зависимости между анализируемыми показателями. Сделанный вывод подтверждает диаграмма рассеяния показателей (рис. 1).
-уровня свидетельствует о том, что коэффициент корреляции не является статистически значимым. Другими словами, имеющиеся данные о среднемесячной заработной плате и доле сбережений населения не позволяют сделать вывод о наличии значимой связи. Выборочное значение коэффициента корреляции следует рассматривать как значение, случайно полученное при формировании выборки, т.е. отклонение от нулевого значения не отражает истинной зависимости между анализируемыми показателями. Сделанный вывод подтверждает диаграмма рассеяния показателей (рис. 1).
Примечание. Следует принять во внимание условность всех сделанных выше выводов, поскольку нормальность распределений рассматриваемых показателей не подтверждается ни одним из критериев согласия. Предварительный вывод можно сделать на основании изучения гистограмм распределения показателей.
Очевидно, что дальнейшее исследование этих данных с помощью регрессионного анализа не имеет смысла. Можно попытаться обнаружить зависимость между показателями, предварительно преобразовав их. Например, перейти к исследованию зависимости между логарифмами этих показателей.
ll. По данным ряда регионов за ноябрь 1997 г. (табл. 3) требуется оценить зависимость потребительских расходов на душу населения (тыс. руб.) от средней заработной платы и выплат социального характера (тыс. руб.).
Таблица 3
Результаты расчета описательных статистик приведены в табл. 4.
| Статистики | ПОТ_РАСХ | СР_ЗП |
| Выборочное среднее | 393,52 | 685,18 |
| Выборочная дисперсия | 7 179,62 | 16 644,78 |
| Выборочное среднее квадратичное отклонение | 84,73 | 129,01 |
| Нижний квартиль | 354 | 577 |
| Верхний квартиль | 432 | 796 |
| Размах выборки | 78 | 219 |
| 95%-ный доверительный интевал для М(Х) | (349,79; 436,92) | (628,84; 761,51) |
| 99%-ный доверительный интевал М(Х) | (333,33; 453,38) | (603,78; 786,57) |
| 95%-ый доверительный интевал для D(Х) | (3 981,76; 16 648,26) | (9 231,07; 38 596,56) |
Выборочный коэффициент корреляции равен 0,58, при этом значение 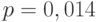 . Такая величина
. Такая величина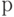 -уровня свидетельствует о том, что коэффициент корреляции является статистически значимым. Другими словами, имеющиеся данные о среднемесячной заработной плате и потребительских расходах на душу населения позволяют говорить о наличии средней статистической связи между этими показателями. Очевидно, что имеет смысл исследовать эту зависимость более детально средствами регрессионного анализа.
-уровня свидетельствует о том, что коэффициент корреляции является статистически значимым. Другими словами, имеющиеся данные о среднемесячной заработной плате и потребительских расходах на душу населения позволяют говорить о наличии средней статистической связи между этими показателями. Очевидно, что имеет смысл исследовать эту зависимость более детально средствами регрессионного анализа.
Построенное уравнение регрессии имеет следующий вид:
Примечание. В скобках приведены стандартные ошибки оценок параметров уравнения регрессии.
Результаты расчета параметров парной регрессии представлены в табл. 5, являющейся выходом модуля Multiple Regression.
Таблица 5
Полученное уравнение регрессии является значимым ( -статистика равняется 7,67 при
-статистика равняется 7,67 при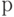 -значении 0,014337). Это означает, что выявленная связь является значимой и построенная модель может быть использована в дальнейшем для экономического анализа и прогноза.
-значении 0,014337). Это означает, что выявленная связь является значимой и построенная модель может быть использована в дальнейшем для экономического анализа и прогноза.
Коэффициент детерминации уравнения 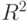 равен 0,338201 (скорректированный 0,294). Это говорит о том, что полученная модель на 34% объясняет (точнее - воспроизводит) общую вариацию (разброс значений) зависимой переменной— потребительских расходов. Коэффициент уравнения регрессии
равен 0,338201 (скорректированный 0,294). Это говорит о том, что полученная модель на 34% объясняет (точнее - воспроизводит) общую вариацию (разброс значений) зависимой переменной— потребительских расходов. Коэффициент уравнения регрессии 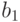 является значимым (
является значимым ( -значение равняется 0,014337), а следовательно, может быть экономически проинтерпретирован. Его величина показывает, что в среднем с увеличением заработанной платы на 1000 руб. потребительские расходы увеличиваются на 381 руб., т.е. приблизительно 38% дополнительной заработной платы тратится на питание.
-значение равняется 0,014337), а следовательно, может быть экономически проинтерпретирован. Его величина показывает, что в среднем с увеличением заработанной платы на 1000 руб. потребительские расходы увеличиваются на 381 руб., т.е. приблизительно 38% дополнительной заработной платы тратится на питание.
Доверительный интервал для этого параметра можно вычислить, учитывая, что 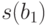 равняется 0,13795 (см. табл. 5), а
равняется 0,13795 (см. табл. 5), а 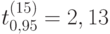 .
.
Таким образом, доверительным интервалом для параметра 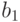 будет интервал (0,092; 0,671). Как видно, этот интервал не содержит нулевого значения, что равносильно выводу о значимости параметра b_{1}.
будет интервал (0,092; 0,671). Как видно, этот интервал не содержит нулевого значения, что равносильно выводу о значимости параметра b_{1}.
Параметр 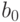 не является значимым, поскольку его
не является значимым, поскольку его  -значение составляет 0,209281, что превышает стандартное значение 0,05. Доверительный интервал для
-значение составляет 0,209281, что превышает стандартное значение 0,05. Доверительный интервал для 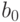 , учитывая, что
, учитывая, что 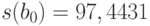 , можно вычислить следующим образом:
, можно вычислить следующим образом: 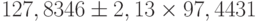 . Полученный интервал (–79,72; 335,38) включает в себя нулевое значение, что равносильно незначимости этого коэффициента, а следовательно, и бессмысленности его экономической интерпретации.
. Полученный интервал (–79,72; 335,38) включает в себя нулевое значение, что равносильно незначимости этого коэффициента, а следовательно, и бессмысленности его экономической интерпретации.
Сделанные выводы о значимости уравнения регрессии подтверждают и результаты дисперсионного анализа (табл. 6).
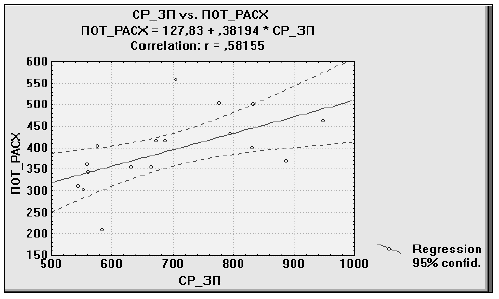
Парное уравнение регрессии, как известно, может быть представлено графически. В данном случае регрессионной модели будет соответствовать уравнение прямой на плоскости. Пакет STATISTICA позволяет получить график этой прямой (рис. 2).
на плоскости. Пакет STATISTICA позволяет получить график этой прямой (рис. 2).
На графике (рис. 2) по горизонтали отложены значения независимой переменной, т.е. средней заработной платы - СР_ЗП, а по вертикали - значения зависимой переменной, т.е. потребительских расходов ПОТ_РАСХ. Точками на плоскости отмечены исходные данные. Прямая линия соответствует регрессионной модели. Выше и ниже прямой расположены линии, обозначающие границы 95%-ного доверительного интервала для прогноза значений зависимой переменной.
Оценка качества полученной модели и все сделанные ранее выводы о значимости параметров, как известно, справедливы лишь при выполнении условий Гаусса - Маркова и требования нормальности распределения случайной составляющей уравнения регрессии. В качестве оценки случайной составляющей рассматриваются остатки построенного уравнения. Поэтому оценка качества полученной модели включает в себя исследование остатков.
График зависимости остатков от величин предсказанных значений зависимой переменной (рис. 3) позволяет оценить характер отклонений наблюдаемых значений от построенного уравнения прямой.
Построенный график показывает, что отклонения наблюдаемых значений от построенной прямой носит случайный характер и не имеет систематических отклонений в какую-либо сторону. Большинство значений остатков не выходит за границы 95%-ного доверительного интервала для расчетных значений зависимой переменной.
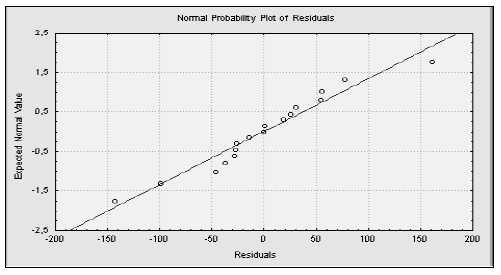
Проверка предположения о нормальности распределения остатков на качественном уровне может быть выполнена путем построения гистограммы остатков. Другой способ визуальной оценки нормальности распределения остатков заключается в построении графика остатков в логарифмической шкале. В случае выполнения предположения о нормальности распределения остатков точки графика должны располагаться вблизи прямой линии. Именно такую ситуацию мы наблюдаем на приводимом ниже графике (рис. 4).
Для расчета прогнозного значения зависимой переменной сначала определим значение независимой переменной. Среднее значение заработной платы составляет 685,18 тыс. руб. (в масштабе цен 1997 г.), в случае увеличения этой величины на 10% получим 753,698 тыс. руб. Подставляя полученное значение в уравнение регрессии (режим Predict Dependent var.), получаем соответствующее расчетное значение, равное 415,7049 тыс. руб.
Границы 95%-ного доверительного интервала для прогнозного значения приближенно можно определить с помощью графика уравнения регрессии.
Считывая координаты соответствующих точек на графике (рис. 4), находим (372; 456).
В этих пределах с вероятностью 0,95 будет находиться среднее значение потребительских расходов в случае, если среднее значение заработной платы составит примерно 415 тыс. руб.
Коэффициент эластичности (средний) для построенного уравнения регрессии составляет 0,66 (0,3814 \cdot 685,18/393,52). Это значит, что с увеличением на 1% среднего значения заработной платы, т.е. на 685,18 тыс. руб., среднее значение потребительских расходов увеличится на 0,66%, т.е. на 2,597 тыс. руб.