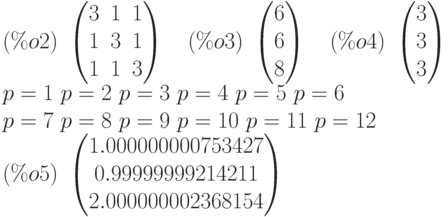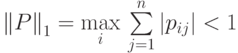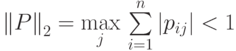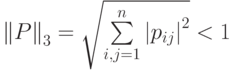НОУ ИНТУИТ | Компьютерная математика с Maxima. Лекция 8: Реализация некоторых численных методов

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Компания ALT Linux

Опубликован: 24.03.2015 | Доступ: свободный | Студентов: 553 / 138 | Длительность: 19:00:00

Темы: Математика, Программное обеспечение, Физика

Специальности: Математик, Преподаватель, Физик

|

Вам нравится? Нравится 20 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

8.4.3 Метод Зейделя

В методе Зейделя система (8.1) также приводится к системе (8.5). Но при вычислении последующей компоненты вектора используются уже вычисленные компоненты этого вектора.

Итерационная формула метода в скалярной форме записывается следующим образом:

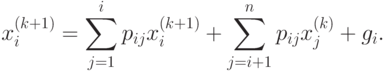
$x_{i}^{(k+1)}=\sum\limits_{j=1}^{i}{{{p}_{ij}}}x_{i}^{(k+1)}+\sum\limits_{ j=i+1}^{n}{{{p}_{ij}}}x_{j}^{(k)}+{{g}_{i}}.$

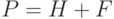Установим связь между методом Зейделя и методом простой итерации. Для этого матрицу представим в виде суммы двух матриц: P = H + F , где

$H=\left[ \begin{matrix} 0 & 0 & 0 & \ldots & 0 \\ {{p}_{21}} & 0 & 0 & \ldots & 0 \\ {{p}_{31}} & {{p}_{32}} & 0 & \ldots & 0 \\ \ldots & \ldots & \ldots & \ldots & \ldots \\ {{p}_{n1}} & {{p}_{n2}} & {{p}_{n3}} & \ldots & 0 \\ \end{matrix} \right]; \quad F=\left[ \begin{matrix} {{p}_{11}} & {{p}_{12}} & {{p}_{13}} & \ldots & {{p}_{1n}} \\ 0 & {{p}_{22}} & {{p}_{23}} & \ldots & {{p}_{2n}} \\ 0 & 0 & {{p}_{33}} & \ldots & {{p}_{3n}} \\ \ldots & \ldots & \ldots & \ldots & \ldots \\ 0 & 0 & 0 & \ldots & {{p}_{nn}} \\ \end{matrix} \right].$

Итерационная формула метода Зейделя в матричной форме записывается в виде:

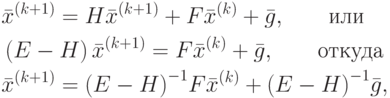
$\begin{align*} &{{\bar{x}}^{(k+1)}}=H{{\bar{x}}^{(k+1)}}+F{{\bar{x}}^{(k)}}+\bar{g}, \qquad \text{или} \\ &\left( E-H \right){{\bar{x}}^{(k+1)}}=F{{\bar{x}}^{(k)}}+\bar{g}, \qquad \text{откуда} \\ &{{\bar{x}}^{(k+1)}}={{\left( E-H \right)}^{-1}}F{{\bar{x}}^{(k)}}+{{\left( E-H \right)}^{-1}}\bar{g}, \end{align*}$

т.е. метод Зейделя эквивалентен методу простой итерации с матрицей $(E - H)^{-1}F$ .

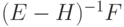Исходя из полученной аналогии методов Зейделя и простой итерации, можно сформулировать следующий признак сходимости метода Зейделя: для того чтобы метод Зейделя сходился, необходимо и достаточно, чтобы все собственные значения матрицы 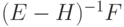$(E - H)^{-1}F$ по модулю были меньше единицы.

Другими словами, чтобы метод Зейделя сходился, необходимо и достаточно, чтобы все корни уравнения по модулю были меньше единицы, т.к.

$\begin{align*} \left| {{\left( E-H \right)}^{-1}}F-\lambda E \right| &= \\ \left| {{\left( E-H \right)}^{-1}}\left( E-H \right)\left[ {{\left( E-H \right)}^{-1}}F-\lambda E \right] \right| &= \\ \left| {{\left( E-H \right)}^{-1}} \right|\left| F+\lambda H-\lambda E \right| &= \\ \left| F+\lambda H-\lambda E \right|&=0. \end{align*}$

Сформулируем достаточный признак сходимости: для того, чтобы метод Зейделя сходился, достаточно, чтобы выполнилось одно из условий:

${{\left\| P \right\|}_{1}}= \underset{i}{\mathop{\max }}\, \sum\limits_{j=1}^{n}{\left|{{p}_{ij}} \right|<1}$
${{\left\| P \right\|}_{2}}= \underset{j}{\mathop{\max}}\, \sum\limits_{i=1}^{n}{\left| {{p}_{ij}} \right|<1}$
${{\left\| P \right\|}_{3}}= \sqrt{\sum\limits_{i,j=1}^{n}{{{\left| {{p}_{ij}}\right|}^{2}}}}<1$

При использовании метода Зейделя итерационный процесс сходится к единственному решению быстрее метода простых итераций.

Пример реализации метода Зейделя:

(%i1)	seidel(a0,b0,x,n,eps):=block([a,b,i,j,s,sum,p],
	a:copymatrix (a0), b:copymatrix(b0),
	sum:1, p:0,
	while sum>eps do (
		sum:0, p:p+1, print("p= ",p),
		for i:1 thru n do
		(
			s:b[i,1],
			for j:1 thru n do (s:s-a[i,j]*x[j,1]),
			s:s/a[i,i], x[i,1]:x[i,1]+s, sum:sum+abs(s)
		)
	),
	float(x))$

Пример решения простой системы методом Зейделя:

(%i2)	aa:matrix([3,1,1],[1,3,1],[1,1,3]); bb:matrix([6],[6],[8]);
	x:matrix([3],[3],[3]); zz:seidel(aa,bb,x,3,0.0000001);

$(\%o2)\ \begin{pmatrix}3 & 1 & 1\cr 1 & 3 & 1\cr 1 & 1 & 3\end{pmatrix} \quad (\%o3)\ \begin{pmatrix}6\cr 6\cr 8\end{pmatrix} \quad (\%o4)\ \begin{pmatrix}3\cr 3\cr 3\end{pmatrix}\\ p= 1 \ p= 2 \ p= 3 \ p= 4 \ p= 5 \ p= 6 \\ p= 7 \ p= 8 \ p= 9 \ p= 10 \ p= 11 \ p= 12\\ (\%o5)\ \begin{pmatrix}1.000000000753427\cr 0.99999999214211\cr 2.000000002368154\end{pmatrix}$

Дальше >>

Авторизоваться

Компьютерная математика с Maxima

Реализация некоторых численных методов

8.4.3 Метод Зейделя

Вопросы и ответы