Численные методы и программирование с Maxima
4.3.5 Численное интегрирование: пакет romberg
Для вычисления определённых интегралов численными методами в Maxima есть простая в использовании и довольно мощная функция 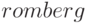 (перед использованием её необходимо загрузить).
(перед использованием её необходимо загрузить).
Синтаксис вызова:
Функция 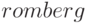 вычисляет определённые интегралы методом Ромберга. В форме
вычисляет определённые интегралы методом Ромберга. В форме 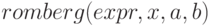 возвращает оценку полного интеграла выражения
возвращает оценку полного интеграла выражения  по переменной
по переменной  в пределах от
в пределах от  до
до  . Выражение
. Выражение  должно возвращать действительное значение (число с плавающей запятой).
должно возвращать действительное значение (число с плавающей запятой).
В форме 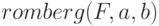 функция возвращает оценку интеграла функции
функция возвращает оценку интеграла функции 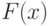 по переменной
по переменной  в пределах от
в пределах от  до
до  (
( представляет собой неназванный, единственный аргумент
представляет собой неназванный, единственный аргумент  ; фактический аргумент может быть отличен от
; фактический аргумент может быть отличен от  ). Функция
). Функция  должна быть функцией Maxima или Lisp, которая возвращает значение с плавающей запятой.
должна быть функцией Maxima или Lisp, которая возвращает значение с плавающей запятой.
Точностью вычислений при выполнении 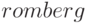 управляют глобальные переменные
управляют глобальные переменные  , и
, и  . Функция
. Функция 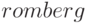 заканчивается успешно, когда абсолютное различие между последовательными приближениями — меньше чем
заканчивается успешно, когда абсолютное различие между последовательными приближениями — меньше чем  , или относительное различие в последовательных приближениях — меньше чем
, или относительное различие в последовательных приближениях — меньше чем  . Таким образом, когда rombergabs равна 0.0 (это значение по умолчанию), только величина относительной ошибки влияет на выполнение функции
. Таким образом, когда rombergabs равна 0.0 (это значение по умолчанию), только величина относительной ошибки влияет на выполнение функции 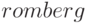 .
.
Функция 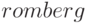 уменьшает шаг интегрирования вдвое по меньшей мере
уменьшает шаг интегрирования вдвое по меньшей мере  раз, поэтому максимальное количество вычислений подинтегральной функции составляет
раз, поэтому максимальное количество вычислений подинтегральной функции составляет  . Если критерий точности интегрирования, установленный
. Если критерий точности интегрирования, установленный  и
и  , не удовлетворен,
, не удовлетворен, 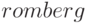 печатает сообщение об ошибке. Функция
печатает сообщение об ошибке. Функция 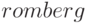 всегда делает по крайней мере
всегда делает по крайней мере  итерации; это — эвристическое правило, предназначенное, чтобы предотвратить преждевременное завершение выполнения функции, когда подинтегральное выражение является колебательным.
итерации; это — эвристическое правило, предназначенное, чтобы предотвратить преждевременное завершение выполнения функции, когда подинтегральное выражение является колебательным.
Вычисление при помощи 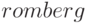 многомерных интегралов возможно, но заложенный разработчиками способ оценки точности приводит к тому, что методы, разработанные специально для многомерных задач, могут привести к той же самой точности с существенно меньшим количеством оценок функции.
многомерных интегралов возможно, но заложенный разработчиками способ оценки точности приводит к тому, что методы, разработанные специально для многомерных задач, могут привести к той же самой точности с существенно меньшим количеством оценок функции.
Рассмотрим примеры вычисления интегралов с использованием 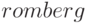 :
:
(%i1) load (romberg);

(%i2) g(x, y) := x*y / (x + y);

(%i3) estimate : romberg (romberg (g(x, y), y, 0, x/2), x, 1, 3);

(%i4) assume (x > 0);
![[x>0]\leqno{(\%o4) }](/sites/default/files/tex_cache/6c69f6b2c1b9acc76ec5fd4b5cdadaef.png)
(%i5) integrate (integrate (g(x, y), y, 0, x/2), x, 1, 3);

(%i6) float(%);

Как видно из полученных результатов вычисления двойного интеграла, точное и приближённое решение совпадают до 7 знака включительно.
