|
Символы кириллицы выводит некорректно. Как сделать чтобы выводился читабельный текст на русском языке? Тип приложения - не Qt, Qt Creator 4.5.0 основан на Qt 5.10.0. Win7.
|
Использование функций при программировании на C++
Задача 4.6. Задано число  в десятичной системе счисления. Выполнить перевод числа в системы счисления с основанием 2, 5 и 7.
в десятичной системе счисления. Выполнить перевод числа в системы счисления с основанием 2, 5 и 7.
Вообще, для того чтобы перевести целое число из десятичной системы счисления в другую, необходимо выполнить следующие действия:
- Разделить данное число на основание новой системы счисления: остаток от деления — младший разряд нового числа;
- Если частное от деления не равно нулю, продолжать деление, как указано в п.1.
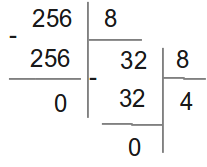
На рис. 4.1 приведён пример "ручного" перевода числа 256, заданного в десятичной системе счисления, в восьмеричную. В результате получим 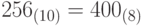
Далее приведён текст программы, реализующей решение задачи 4.6.
#include <iostream>
using namespace std;
unsigned long long int NC( unsigned long long int N, unsigned int b )
{
unsigned long long int S, P;
for ( S=0,P=1;N!=0; S+=N%b *P, P*=10,N/=b );
return S;
}
int main ( )
{
unsigned long long int X;
cout<<"X="; cin >>X; //Ввод числа X.
//Перевод числа X в заданные системы счисления.
cout<<X<<" (10) ="<<NC(X, 2 )<<" (2) "<<endl;
cout<<X<<" (10) ="<<NC(X, 5 )<<" (5) "<<endl;
cout<<X<<" (10) ="<<NC(X, 7 )<<" (7) "<<endl;
return 0;
}
Задача 4.7. Найти корни уравнения 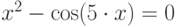 .
.
Для решения задачи использовать:
- метод половинного деления,
- метод хорд,
- метод касательных (метод Ньютона),
- метод простой итерации.
Оценить степень точности предложенных численных методов, определив, за сколько итераций был найден корень уравнения. Вычисления проводить с точностью 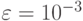 .
.
Вообще говоря, аналитическое решение уравнения
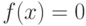 |
( 4.1) |
Интервал можно выделить, изобразив график функции, или каким-либо другим способом. Но все способы основаны на следующем свойстве непрерывной функции: если функция 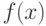 непрерывна на интервале [
непрерывна на интервале [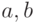 ] и на его концах имеет различные знаки,
] и на его концах имеет различные знаки, 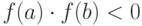 , то между точками имеется хотя бы один корень. Будем считать интервал настолько малым, что в нём находится только один корень. Рассмотрим самый простой способ уточнения корней.
, то между точками имеется хотя бы один корень. Будем считать интервал настолько малым, что в нём находится только один корень. Рассмотрим самый простой способ уточнения корней.
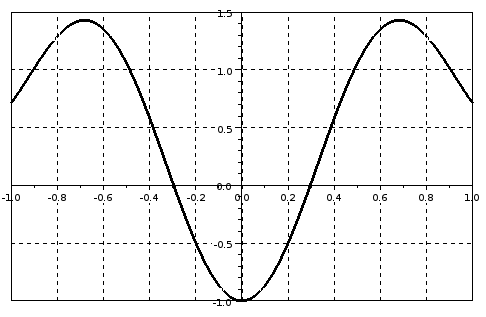
Графическое решение задачи 4.7 показано на рис. 4.2. Так как функция 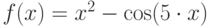 дважды пересекает ось абсцисс, можно сделать вывод о наличии в уравнении
дважды пересекает ось абсцисс, можно сделать вывод о наличии в уравнении 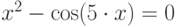 двух корней. Первый находится на интервале [-0.4; -0.2], второй принадлежит отрезку [0.2; 0.4] .
двух корней. Первый находится на интервале [-0.4; -0.2], второй принадлежит отрезку [0.2; 0.4] .
Рассмотрим предложенные в задаче численные методы решения нелинейных уравнений.
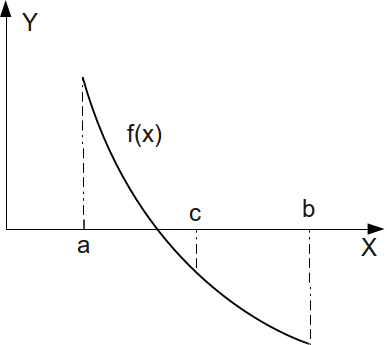
Метод половинного деления (дихотомии). Пусть был выбран интервал изоляции [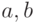 ] (рис. 4.3). Примем за первое приближение корня точку c, которая является серединой отрезка [
] (рис. 4.3). Примем за первое приближение корня точку c, которая является серединой отрезка [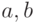 ].Далее будем действовать по следующему алгоритму:
].Далее будем действовать по следующему алгоритму:
- Находим точку
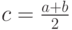 ;
; - Находим значение
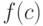 ;
; - Если
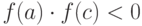 , то корень лежит на интервале [
, то корень лежит на интервале [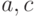 ], иначе корень лежит на интервале [
], иначе корень лежит на интервале [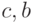 ];
]; - Если величина интервала меньше либо равна
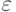 , то найден корень с точностью
, то найден корень с точностью 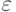 , иначе возвращаемся к п.1.
, иначе возвращаемся к п.1.
Итак, для вычисления одного из корней уравнения 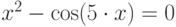 методом половинного деления достаточно знать интервал изоляции корня
методом половинного деления достаточно знать интервал изоляции корня  и точность вычисления
и точность вычисления 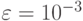 .
.
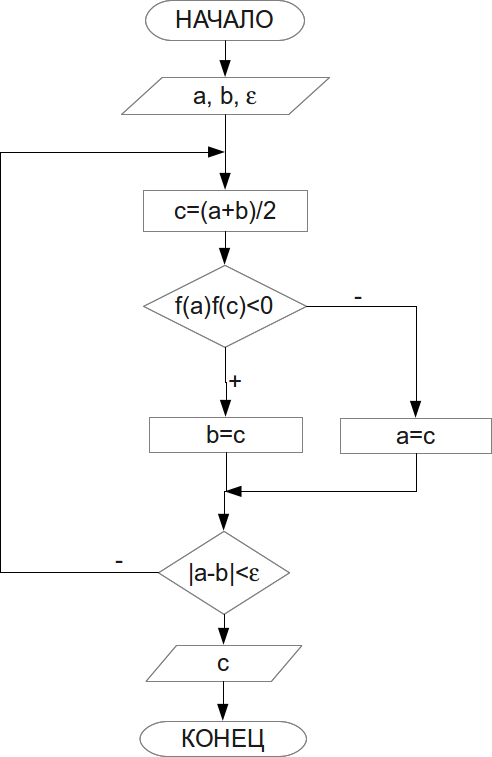
Блок-схема алгоритма решения уравнения методом дихотомии приведена на рис. 4.4. Понятно, что здесь  — корень заданного уравнения.
— корень заданного уравнения.
Однако, несмотря на простоту, такое последовательное сужение интервала проводится редко, так как требует слишком большого количества вычислений.
Кроме того, этот способ не всегда позволяет найти решение с заданной точностью. Рассмотрим другие способы уточнения корня. При применении этих способов будем требовать, чтобы функция 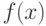 удовлетворяла следующим условиям на интервале [
удовлетворяла следующим условиям на интервале [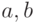 ] :
] :
- функция
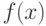 непрерывна вместе со своими производными первого и второго порядка. Функция
непрерывна вместе со своими производными первого и второго порядка. Функция 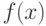 на концах интервала [
на концах интервала [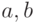 ] имеет разные знаки
] имеет разные знаки 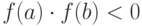 ;
; - первая и вторая производные
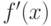 и
и 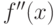 сохраняют определённый знак на всём интервале [
сохраняют определённый знак на всём интервале [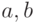 ] .
] .
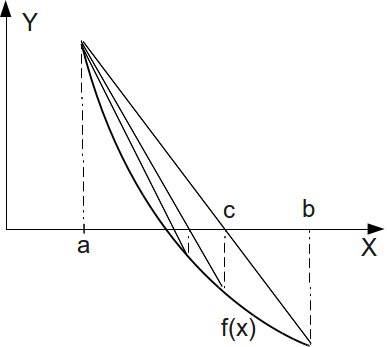
Метод хорд. Этот метод отличается от метода дихотомии тем, что очередное приближение берём не в середине отрезка, а в точке пересечения с осью  (рис. 4.5) прямой, соединяющей точки (
(рис. 4.5) прямой, соединяющей точки (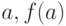 ) и (
) и (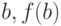 ).
).
Запишем уравнение прямой, проходящей через точки с координатами (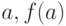 ) и (
) и (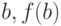 ) :
) :
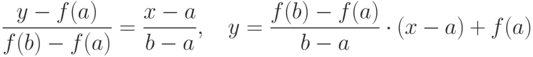 |
( 4.2) |
Прямая, заданная уравнением (4.2), пересекает ось  при условии
при условии  .
.
Найдём точку пересечения хорды с осью  :
: 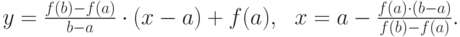 итак,
итак, 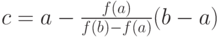 .
.
Далее необходимо вычислить значение функции в точке  . Это и будет приближённое значение корня уравнения.
. Это и будет приближённое значение корня уравнения.
Для вычисления одного из корней уравнения 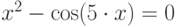 методом хорд достаточно знать интервал изоляции корня, например,
методом хорд достаточно знать интервал изоляции корня, например,  , и точность вычисления
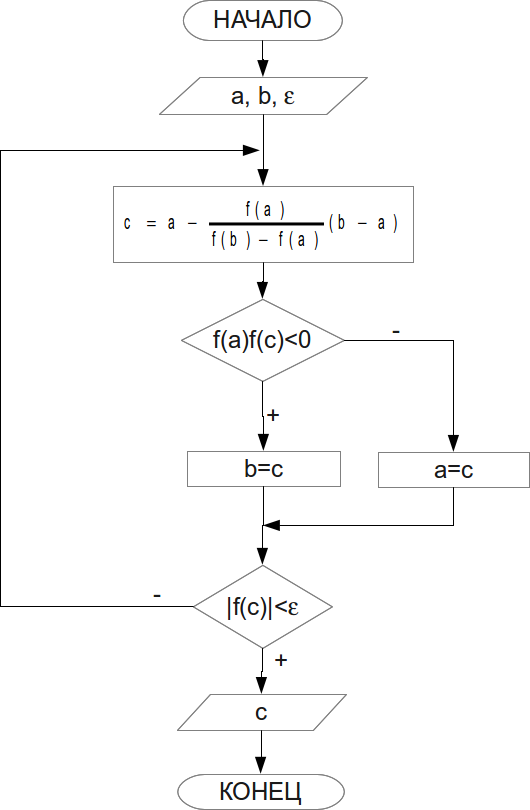
, и точность вычисления 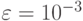 . Блок-схема метода представлена на рис. 4.6.
. Блок-схема метода представлена на рис. 4.6.
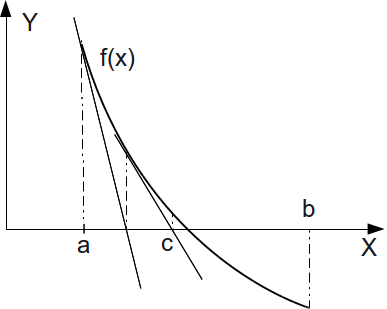
Метод касательных (метод Ньютона). В одной из точек интервала [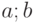 ], пусть это будет точка
], пусть это будет точка  , проведём касательную (рис. 4.7). Запишем уравнение этой прямой:
, проведём касательную (рис. 4.7). Запишем уравнение этой прямой:
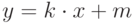 |
( 4.3) |
Так как эта прямая является касательной, и она проходит через точку 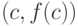 , то
, то 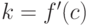 .
.
Следовательно, 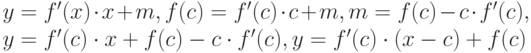 .
.
Найдём точку пересечения касательной с осью  :
: 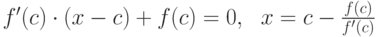
Если 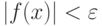 , то точность достигнута, и точка
, то точность достигнута, и точка  — решение; иначе необходимо переменной c присвоить значение
— решение; иначе необходимо переменной c присвоить значение  и провести касательную через новую точку
и провести касательную через новую точку  ; так продолжать до тех пор, пока
; так продолжать до тех пор, пока 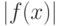 не станет меньше
не станет меньше 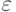 . Осталось решить вопрос, что выбрать в качестве точки начального приближения
. Осталось решить вопрос, что выбрать в качестве точки начального приближения  .
.
В этой точке должны совпадать знаки функции и её второй производной. А так как нами было сделано допущение, что вторая и первая производные не меняют знак, то можно проверить условие 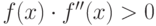 на обоих концах интервала, и в качестве начального приближения взять ту точку, где это условие выполняется.
на обоих концах интервала, и в качестве начального приближения взять ту точку, где это условие выполняется.
Здесь, как и в предыдущих методах, для вычисления одного из корней уравнения 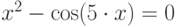 достаточно знать интервал изоляции корня, например,
достаточно знать интервал изоляции корня, например,  , и точность вычисления
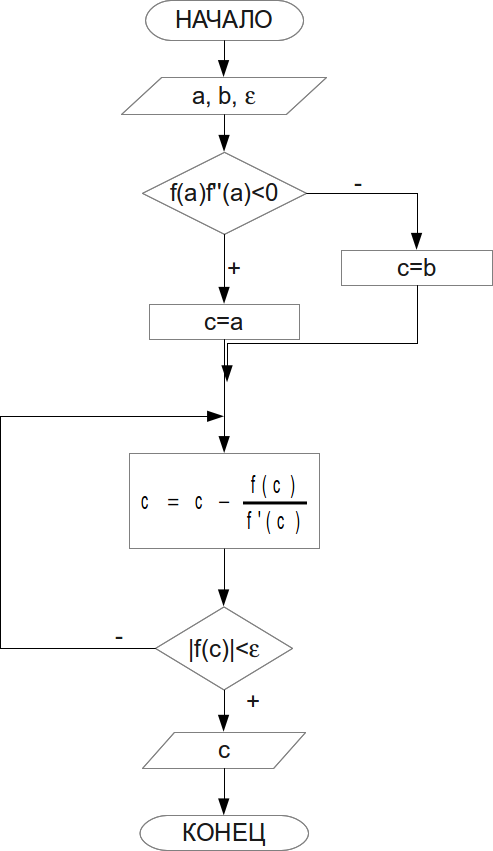
, и точность вычисления 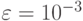 . Блок-схема метода Ньютона представлена на рис. 4.8. Понятно, что для реализации этого алгоритма нужно найти первую и вторую производные функции
. Блок-схема метода Ньютона представлена на рис. 4.8. Понятно, что для реализации этого алгоритма нужно найти первую и вторую производные функции 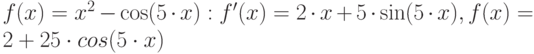 .
.
Метод простой итерации. Для решения уравнения этим методом необходимо записать уравнение (4.1) в виде 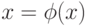 , задать начальное приближение
, задать начальное приближение ![x_0\in [a;b]](/sites/default/files/tex_cache/03b0647793481b87775cde08b2b0f83a.png) и организовать следующий итерационный вычислительный процесс:
и организовать следующий итерационный вычислительный процесс: 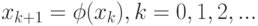
Вычисление прекратить, если 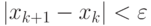 (
(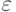 — точность).
— точность).
Если неравенство 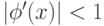 выполняется на всём интервале [
выполняется на всём интервале [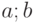 ], то последовательность
], то последовательность  сходится к решению
сходится к решению 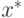 (т.е. l
(т.е. l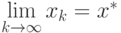 ).
).
Значение функции 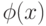 должно удовлетворять условию
должно удовлетворять условию 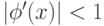 для того, чтобы можно было применить метод простых итераций. Условие
для того, чтобы можно было применить метод простых итераций. Условие 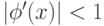 является достаточным условием сходимости метода простой итерации.
является достаточным условием сходимости метода простой итерации.
Уравнение (4.1) можно привести к виду 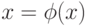 следующим образом. Умножить обе части уравнения
следующим образом. Умножить обе части уравнения 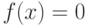 на число
на число  . К обеим частям уравнения
. К обеим частям уравнения 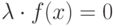 добавить число
добавить число  . Получим
. Получим 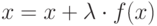 . Это и есть уравнение вида
. Это и есть уравнение вида 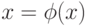 , где
, где
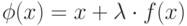 |
( 4.4) |
Необходимо чтобы неравенство  выполнялось на интервале [
выполнялось на интервале [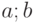 ], следовательно,
], следовательно, 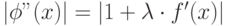 и
и 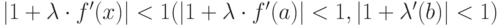 , а значит, с помощью подбора параметра
, а значит, с помощью подбора параметра  можно добиться выполнения условия сходимости.
можно добиться выполнения условия сходимости.
Для вычисления корней уравнения 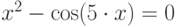 воспользуемся графическим решением (рис. 4.2) и определим интервал изоляции одного из корней, например,
воспользуемся графическим решением (рис. 4.2) и определим интервал изоляции одного из корней, например,  . Подберём значение
. Подберём значение  , решив неравенство
, решив неравенство 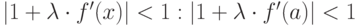 и
и 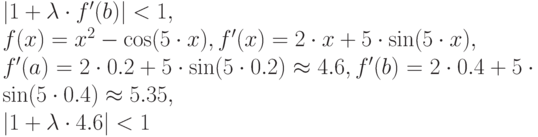 и
и 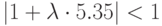 .
.
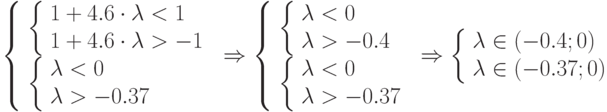
и, следовательно, 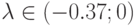 .
.
Таким образом, исходными данными для программы будут начальное значение корня уравнения 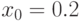 , значение параметра
, значение параметра  (пусть
(пусть 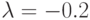 ), и точность вычислений
), и точность вычислений 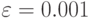 .
.
Для вычисления второго корня заданного уравнения параметр  подбирают аналогично.
подбирают аналогично.
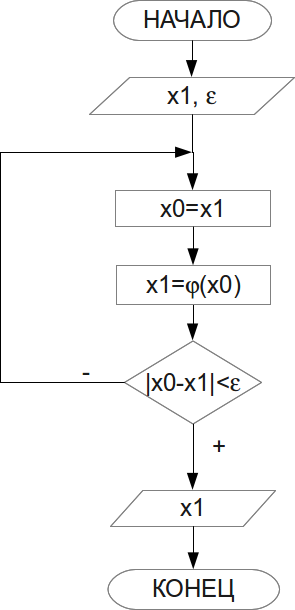
Блок-схема метода простой итерации приведена на рис. 4.9.
Далее представлен текст программы, реализующий решение задачи 4.7.
#include <iostream>
#include <math.h>
using namespace std;
//Функция, определяющая левую часть уравнения f (x) = 0.
double f ( double x )
{
return ( x *x-cos (5 * x ) );
}
//Функция, реализующая метод половинного деления.
int Dichotomy ( double a, double b, double * c, double eps )
{ int k=0;
do
{
* c=(a+b ) / 2;
if ( f ( * c ) * f ( a ) <0) b=*c;
else a=*c;
k++;
}
while ( fabs ( a-b )>=eps );
return k;
}
//Функция, реализующая метод хорд.
int Chord ( double a, double b, double * c, double eps )
{ int k=0;
do
{
* c=a-f ( a ) /( f ( b )-f ( a ) ) * ( b -a );
if ( f ( * c ) * f ( a ) >0) a=*c;
else b=*c;
k++;
}
while ( fabs ( f ( * c ) )>=eps );
return k;
}
double f1 ( double x ) //Первая производная функции f (x).
{
return (2 * x+5* sin (5 * x ) );
}
double f2 ( double x ) //Вторая производная функции f (x).
{
return (2+25* cos (5 * x ) );
}
//Функция, реализующая метод касательных.
int Tangent ( double a, double b, double * c, double eps )
{ int k=0;
if ( f ( a ) * f2 ( a ) >0) * c=a;
else * c=b;
do
{
* c=*c-f (* c ) / f1 ( * c );
k++;
}
while ( fabs ( f ( * c ) )>=eps );
return k;
}
double fi ( double x, double L) //Функция, заданная выражением 4.4 .
{
return ( x+L* f ( x ) );
}
//Функция, реализующая метод простой итерации.
int Iteration ( double *x, double L, double eps )
{ int k=0; double x0;
do
{
x0=*x;
*x= fi(x0, L);
k++;
}
while ( fabs ( x0-*x )>=eps );
return k;
}
int main ( )
{
double A, B, X, P;
double ep =0.001; //Точность вычислений.
int K;
cout<<"a="; cin >>A; //Интервал изоляции корня.
cout<<"b="; cin >>B;
cout<<"Решение уравнения x^2 - cos (5* x) =0. "<<endl;
cout<<"Метод дихотомии:"<<endl;
K=Dichotomy (A, B,&X, ep );
cout<<"Найденное решение x="<<X;
cout<<", количество итераций k="<<K<<endl;
cout<<"Метод хорд:"<<endl;
K=Chord (A, B,&X, ep );
cout<<" Найденное решение x="<<X;
cout<<", количество итераций k="<<K<<endl;
cout<<"Метод касательных:"<<endl;
K=Tangent (A, B,&X, ep );
cout<<" Найденное решение x="<<X;
cout<<", количество итераций k="<<K<<endl;
cout<<"Метод простой итерации:"<<endl;
X=A;
cout<<"L="; cin >>P;
K=Iteration (&X, P, ep );
cout<<" Найденное решение x="<<X;
cout<<", количество итераций k="<<K<<endl;
return 0;
}
Результаты работы программы:
a=0.2 b=0.4 Решение уравнения x^2-cos(5*x)=0. Метод дихотомии: Найденное решение x=0.296094, количество итераций k=8 Метод хорд: Найденное решение x=0.296546, количество итераций k=2 Метод касательных: Найденное решение x=0.296556, количество итераций k=2 Метод простой итерации: L=-0.2 Найденное решение x=0.296595, количество итераций k=3