|
Символы кириллицы выводит некорректно. Как сделать чтобы выводился читабельный текст на русском языке? Тип приложения - не Qt, Qt Creator 4.5.0 основан на Qt 5.10.0. Win7.
|
Использование функций при программировании на C++
4.10 Задачи для самостоятельного решения
4.10.1 Применение функций при работе с последовательностями чисел
Разработать программу на языке C++ для следующих заданий:
- Вводится последовательность целых положительных чисел, 0 — конец последовательности. Для каждого элемента последовательности определить и вывести на экран число, которое получится после записи цифр исходного числа в обратном порядке.
- Вводится последовательность целых чисел, 0 — конец последовательности. Определить, содержит ли последовательность хотя бы одно совершённое число. Совершённое число равно сумме всех своих делителей, не превосходящих это число. Например, 6 = 1 + 2 + 3 или 28 = 1 + 2 + 4 + 7 + 14.
- Вводится последовательность из N целых положительных элементов. Определить, содержит ли последовательность хотя бы одно простое число. Простое число не имеет делителей, кроме единицы и самого себя.
- Вводится последовательность из
 целых положительных элементов. Посчитать количество чисел-палиндромов. Числа-палиндромы симметричны относительно своей середины, например, 12021 или 454.
целых положительных элементов. Посчитать количество чисел-палиндромов. Числа-палиндромы симметричны относительно своей середины, например, 12021 или 454. - Вводится последовательность из
 целых положительных элементов. Подсчитать количество совершённых и простых чисел в последовательности.
целых положительных элементов. Подсчитать количество совершённых и простых чисел в последовательности. - Поступает последовательность целых положительных чисел, 0 — конец последовательности. Определить, в каком из чисел больше всего делителей.
- Поступает последовательность целых положительных чисел, 0 — конец последовательности. Определить, в каком из чисел больше всего цифр.
- Вводится последовательность из
 целых положительных элементов. Проверить, содержит ли последовательность хотя бы одну пару соседних дружественных чисел. Два различных натуральных числа являются дружественными, если сумма всех делителей первого числа (кроме самого числа) равна второму числу. Например, 220 и 284, 1184 и 1210, 2620 и 2924, 5020 и 5564.
целых положительных элементов. Проверить, содержит ли последовательность хотя бы одну пару соседних дружественных чисел. Два различных натуральных числа являются дружественными, если сумма всех делителей первого числа (кроме самого числа) равна второму числу. Например, 220 и 284, 1184 и 1210, 2620 и 2924, 5020 и 5564. - Поступает последовательность целых положительных чисел, 0 — конец последовательности. Каждый элемент последовательности представляет собой номер m одного из чисел Фибоначчи. Вычислить и вывести на экран m-е число Фибоначчи. Напомним, что в последовательности Фибоначчи каждое последующее число представляет собой сумму двух предыдущих (0, 1, 1, 2, 3, 5, 8, 13, 21, 34,...). Например, четвёртое число Фибоначчи равно 3, седьмое — 13, а девятое — 34.
- Вводится последовательность из
 целых положительных элементов. Найти число с минимальным количеством цифр.
целых положительных элементов. Найти число с минимальным количеством цифр. - Вводится последовательность из
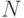 целых элементов. Для всех положительных элементов последовательности вычислить значение факториала. Вывести на экран число и его факториал.
целых элементов. Для всех положительных элементов последовательности вычислить значение факториала. Вывести на экран число и его факториал. - Поступает последовательность целых положительных чисел, 0 — конец последовательности. Вывести на экран все числа последовательности, являющиеся составными и их делители. Составное число имеет более двух делителей, то есть не является простым.
- Вводится последовательность из
 целых положительных элементов. Определить, содержит ли последовательность хотя бы одно число Армстронга. Число Армстронга — натуральное число, которое равно сумме своих цифр, возведённых в степень, равную количеству его цифр. Например, десятичное число 153 — число Армстронга, потому что: 13+ 33+ 53=1 + 27 + 125 = 153.
целых положительных элементов. Определить, содержит ли последовательность хотя бы одно число Армстронга. Число Армстронга — натуральное число, которое равно сумме своих цифр, возведённых в степень, равную количеству его цифр. Например, десятичное число 153 — число Армстронга, потому что: 13+ 33+ 53=1 + 27 + 125 = 153. - Поступает последовательность целых положительных чисел, 0 — конец последовательности. Найти среднее арифметическое простых чисел в этой последовательности. Простое число не имеет делителей, кроме единицы и самого себя.
- Вводится последовательность из
 целых положительных элементов. Определить, сколько в последовательности пар соседних взаимно простых чисел. Различные натуральные числа являются взаимно простыми, если их наибольший общий делитель равен единице.
целых положительных элементов. Определить, сколько в последовательности пар соседних взаимно простых чисел. Различные натуральные числа являются взаимно простыми, если их наибольший общий делитель равен единице. - В последовательности из
 целых положительных элементов найти сумму всех недостаточных чисел. Недостаточное число всегда больше суммы всех своих делителей за исключением самого числа.
целых положительных элементов найти сумму всех недостаточных чисел. Недостаточное число всегда больше суммы всех своих делителей за исключением самого числа. - Вводится последовательность из
 целых положительных элементов. Посчитать количество элементов последовательности, имеющих в своём представлении цифру 0.
целых положительных элементов. Посчитать количество элементов последовательности, имеющих в своём представлении цифру 0. - Вводится
 пар целых положительных чисел
пар целых положительных чисел  и
и  . В случае, если
. В случае, если 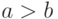 вычислить:
вычислить: 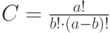 .
. - Вводится последовательность из
 целых элементов. Для каждого элемента последовательности найти среднее значение его цифр.
целых элементов. Для каждого элемента последовательности найти среднее значение его цифр. - Вводится последовательность целых положительных чисел, 0 — конец последовательности. Для каждого элемента последовательности определить и вывести на экран число, которое получится, если поменять местами первую и последнюю цифры исходного числа.
- Вводится последовательность из
 целых элементов. Для каждого элемента последовательности вывести на экран количество цифр и количество делителей.
целых элементов. Для каждого элемента последовательности вывести на экран количество цифр и количество делителей. - Вводится последовательность из
 целых положительных элементов. Среди элементов последовательности найти наибольшее число-палиндром. Числа-палиндромы симметричны относительно своей середины, например, 12021 или 454.
целых положительных элементов. Среди элементов последовательности найти наибольшее число-палиндром. Числа-палиндромы симметричны относительно своей середины, например, 12021 или 454. - Поступает последовательность целых положительных чисел, 0 — конец последовательности. Для каждого элемента последовательности вывести на экран сумму квадратов его цифр.
- Вводится последовательность из
 целых положительных элементов. Для простых элементов последовательности определить сумму цифр. Простое число не имеет делителей, кроме единицы и самого себя.
целых положительных элементов. Для простых элементов последовательности определить сумму цифр. Простое число не имеет делителей, кроме единицы и самого себя. - Вводится последовательность целых положительных чисел, 0 — конец последовательности. Среди элементов последовательности найти наименьшее составное число. Составное число имеет более двух делителей, то есть не является простым.
4.10.2 Применение функций для вычислений в различных системах счисления
Разработать программу на языке C++ для решения следующей задачи. Заданы два числа —  и
и  , первое в системе счисления с основанием
, первое в системе счисления с основанием  , второе в системе счисления с основанием
, второе в системе счисления с основанием  . Вычислить значение
. Вычислить значение 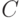 по указанной формуле и вывести его на экран в десятичной системе счисления и системе счисления с основанием
по указанной формуле и вывести его на экран в десятичной системе счисления и системе счисления с основанием  . Исходные данные для решения задачи представлены в табл. 4.1.
. Исходные данные для решения задачи представлены в табл. 4.1.
| Вариант | p | q | C | r |
|---|---|---|---|---|
| 1 | 2 | 8 | 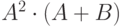 |
3 |
| 2 | 3 | 4 | 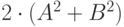 |
4 |
| 3 | 4 | 6 | 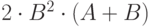 |
5 |
| 4 | 5 | 2 | 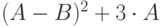 |
6 |
| 5 | 6 | 4 | 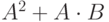 |
7 |
| 6 | 7 | 3 | 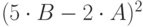 |
8 |
| 7 | 8 | 2 | 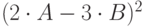 |
5 |
| 8 | 3 | 8 | 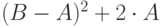 |
6 |
| 9 | 4 | 7 | 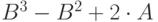 |
2 |
| 10 | 5 | 6 | 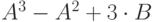 |
8 |
| 11 | 6 | 5 | 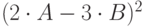 |
3 |
| 12 | 7 | 4 | 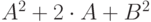 |
5 |
| 13 | 8 | 3 | 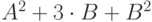 |
7 |
| 14 | 4 | 2 | 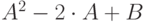 |
6 |
| 15 | 5 | 8 | 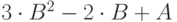 |
3 |
| 16 | 6 | 7 | 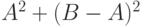 |
2 |
| 17 | 7 | 6 | 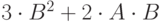 |
8 |
| 18 | 8 | 5 | 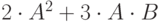 |
7 |
| 19 | 2 | 4 | 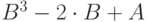 |
3 |
| 20 | 3 | 8 | 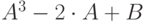 |
4 |
| 21 | 4 | 7 | 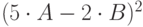 |
5 |
| 22 | 5 | 6 | 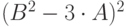 |
7 |
| 23 | 6 | 5 | 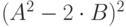 |
8 |
| 24 | 7 | 4 | 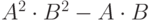 |
6 |
| 25 | 8 | 3 | 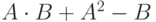 |
2 |
4.10.3 Применение функций для решения нелинейных уравнений
Разработать программу на языке C++ для вычисления одного из корней уравнения 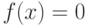 методами, указанными в задании. Для решения задачи предварительно определить интервал изоляции корня графическим методом. Вычисления проводить с точностью
методами, указанными в задании. Для решения задачи предварительно определить интервал изоляции корня графическим методом. Вычисления проводить с точностью 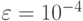 . Оценить степень точности путём подсчёта количества итераций, выполненных для достижения заданной точности. Исходные данные для решения задачи представлены в табл. 4.2.
. Оценить степень точности путём подсчёта количества итераций, выполненных для достижения заданной точности. Исходные данные для решения задачи представлены в табл. 4.2.
| № | Уравнение f (x) = 0 | Методы решения |
|---|---|---|
| 1 | 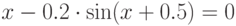 |
метод половинного деления, метод хорд |
| 2 | 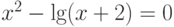 |
метод касательных, метод простой итерации |
| 3 |  |
метод хорд, метод касательных |
| 4 | 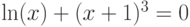 |
метод дихотомии, метод простой итерации |
| 5 |  |
метод половинного деления, метод касательных |
| 6 | 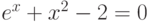 |
метод хорд, метод простой итерации |
| 7 | 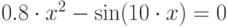 |
метод половинного деления, метод хорд |
| 8 | 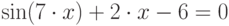 |
метод касательных, метод простой итерации |
| 9 | 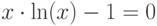 |
метод хорд, метод касательных |
| 10 | 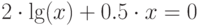 |
метод дихотомии, метод простой итерации |
| 11 | 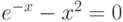 |
метод половинного деления, метод касательных |
| 12 |  |
метод хорд, метод простой итерации |
| 13 | 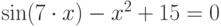 |
метод половинного деления, метод хорд |
| 14 | 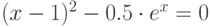 |
метод касательных, метод простой итерации |
| 15 | 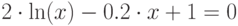 |
метод хорд, метод касательных |
| 16 | 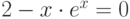 |
метод дихотомии, метод простой итерации |
| 17 | 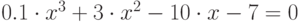 |
метод половинного деления, метод касательных |
| 18 | 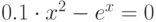 |
метод хорд, метод простой итерации |
| 19 | 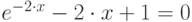 |
метод половинного деления, метод хорд |
| 20 | 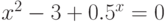 |
метод касательных, метод простой итерации |
| 21 | 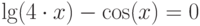 |
метод хорд, метод касательных |
| 22 |  |
метод дихотомии, метод простой итерации |
| 23 | 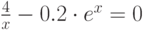 |
метод половинного деления, метод касательных |
| 24 | 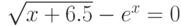 |
метод хорд, метод простой итерации |
| 25 | 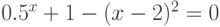 |
метод половинного деления, метод хорд |
