Представление графической информации
Годографом параметрической кривой r(t) = (x(t); y(t)), компоненты которой являются полиномами, называется кривая 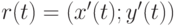 .
.
Таким образом, кривая Безье, построенная по n точкам  , является годографом исходной кривой Безье, построенной по точкам
, является годографом исходной кривой Безье, построенной по точкам  .
.
Пример 20. Годографом квадратичной кривой Безье
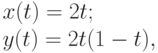
где 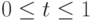
(см. пример 16), является кривая x(t) = 2; y(t) = 2 - 4t, при 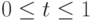 , которая представляет собой отрезок прямой x = 2 для -
, которая представляет собой отрезок прямой x = 2 для -  (рис. 3.23).
(рис. 3.23).
Пример 21. На рис. 3.24 показаны кубическая кривая Безье (справа) и ее годограф - квадратичная кривая Безье (слева).
Отметим также, что в 3D-графике, кроме кривых Безье, используются поверхности Безье.
B-сплайны
B-сплайны являются обобщениями кривых Безье.
Последовательность действительных чисел  , таких что
, таких что  , называется узловым вектором, а сами эти числа - узлами.
, называется узловым вектором, а сами эти числа - узлами.
Для заданного узлового вектора T положим:

для k > 0 (считается, что  ).
).
Функции 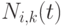 называются базисными функциями степени k.
называются базисными функциями степени k.
Например, при k = 1 и  имеем:
имеем:
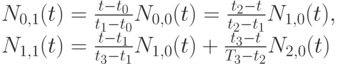
Пусть  - попарно различные точки плоскости.
- попарно различные точки плоскости.
B-сплайном, или базисным сплайном степени k называется кривая

для  и
и ![t \in [t_k; t_{n + 1}]](/sites/default/files/tex_cache/83e718ca40692729f36badfc553fd037.png) , где базисные функции определены на узловом векторе T, который содержит n + k + 2 узлов:
, где базисные функции определены на узловом векторе T, который содержит n + k + 2 узлов:  .
.
Пример 22. Пусть n = k = 1 и T = (0, 0, 1, 1), так что имеются две точки 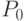 и
и 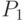 и узлы
и узлы 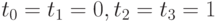 . Тогда
. Тогда

для ![t \in [0;1]](/sites/default/files/tex_cache/08231b9e1b6dbcb828f39cd3ae459f7d.png)

По приведенным выше формулам получаем, что для ![t \in [0; 1]](/sites/default/files/tex_cache/73d01ee9450b0b5d3bb5cbb3e5e58ac2.png)

и

Поэтому B-сплайн первой степени для точек 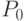 и
и 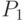 описывается в виде
описывается в виде  , и для
, и для ![t \in [0; 1]](/sites/default/files/tex_cache/73d01ee9450b0b5d3bb5cbb3e5e58ac2.png) представляет собой отрезок, соединяющий точки
представляет собой отрезок, соединяющий точки 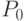 и
и 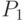 .
.
В общем случае B-сплайн степени k, для  , совпадает при
, совпадает при ![t \in [0; 1]](/sites/default/files/tex_cache/73d01ee9450b0b5d3bb5cbb3e5e58ac2.png) с кривой Безье, если n = k, а узловой вектор имеет вид:
с кривой Безье, если n = k, а узловой вектор имеет вид:

Пример 23. Пусть n = 3, k = 1 и T = (0, 0, 1, 2, 3, 3). Построим B-сплайн первой степени по 4 точкам 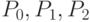 и
и 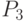 :
:

Имеем:  ,
,  ,
,  ,
,  . Следовательно,
. Следовательно,

для ![t \in [0;3]](/sites/default/files/tex_cache/98cb9028ee7fed603e12544aa075dd5a.png)

Поэтому
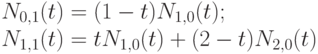
Далее,
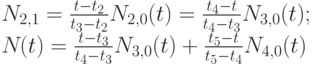
В нашем примере

Таким образом, B-сплайн описывается в виде:

При ![t \in [0; 3]](/sites/default/files/tex_cache/3a8eb0dc05228298a287f4074bfc069b.png) он представляет собой ломаную с вершинами
он представляет собой ломаную с вершинами 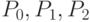 и
и 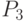 (рис. 3.25).
(рис. 3.25).
Такая же ломаная получается при ![t \in [1; 4]](/sites/default/files/tex_cache/2bb40e5a53c524ec372f455c1627374a.png) , если в качестве узлового вектора взять (0, 1, 2, 3, 4, 5).
, если в качестве узлового вектора взять (0, 1, 2, 3, 4, 5).
Пример 24. Пусть n = 3, k = 2 и T = (0, 0, 0, 1, 3, 3, 3). Построим B-сплайн второй степени по 4 точкам 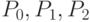 и
и 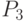 :
:
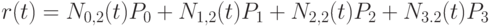
Имеем:  ,
,  . Поэтому
. Поэтому
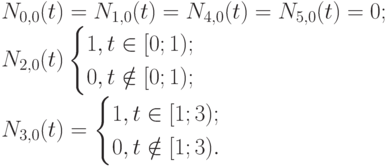
Следовательно, 

Далее,

Поэтому

так как 



