Кодирование чисел и текста
Современные компьютеры могут обрабатывать только дискретную информацию, поэтому любой вид информации преобразуется в числовую форму, которая затем кодируется в двоичном виде.
Кодированием данных называется представление данных с помощью условных знаков. Система двоичного кодирования заключается в представлении данных произвольного типа двоичным кодом, в виде последовательности нулей и единиц.
В настоящей главе рассматриваются методы двоичного кодирования целых и действительных чисел, а также текстовой информации.
В сокращенном виде двоичный код представляется в шестнадцатеричном формате, для этого используются таблицы тетрад. Шестнадцатеричный формат обозначается hex, от hexadecimal, десятичный - dec или decimal.
Кодирование целых чисел
Рассмотрим способы кодирования целых чисел. Для кодирования используется не менее 1 байта, или 8 двоичных разрядов. Типы данных, в которых хранятся целые числа, обычно состоят из 1, 2, 4 или 8 байт.
Кодирование целых неотрицательных чисел
Рассмотрим типы данных, в которых хранятся целые неотрицательные, или беззнаковые, числа. С помощью k двоичных разрядов может быть представлено 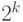 различных значений, с кодами от 00\dots0 до 11\dots1, поэтому в них хранятся целые числа в пределах от 0 до
различных значений, с кодами от 00\dots0 до 11\dots1, поэтому в них хранятся целые числа в пределах от 0 до 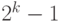 . Диапазоны целых беззнаковых чисел для таких типов данных, а также максимальные числа, которые в них представлены, показаны в табл. 2.1.
. Диапазоны целых беззнаковых чисел для таких типов данных, а также максимальные числа, которые в них представлены, показаны в табл. 2.1.
| Число байт | Диапазон | Максимальное число |
|---|---|---|
| 1 | от 0 до 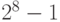
|
255 |
| 2 | от 0 до 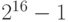
|
65535 |
| 4 | от 0 до 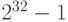
|
4294967295 |
| 8 | от 0 до 
|
18446744073709551615 |
Пример 1. В четырех байтах число 33 кодируется в виде:  , или 00000021 (hex).
, или 00000021 (hex).
Кодирование целых чисел со знаком
Рассмотрим типы данных, которые используются для хранения положительных и отрицательных целых чисел, или целых чисел со знаком. Диапазоны чисел для этих типов данных, которые можно закодировать с помощью 1, 2, 4 или 8 байт, а также минимальные и максимальные числа показаны в таблице 2.2. В первом столбце указывается число байт.
| Диапазон | Минимальное число | Максимальное число | |
|---|---|---|---|
| 1 | от 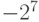 до до 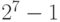
|
- 128 | 127 |
| 2 | от  до до 
|
- 32768 | 32767 |
| 4 | от 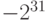 до до 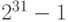
|
- 2147483648 | 2147483647 |
| 8 | от 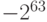 до до 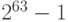
|
- 9223372036854775808 |
Если количество разрядов в типе данных равно k, то диапазон кодируемых чисел составляет от 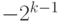 до
до  . Неотрицательные числа кодируются так же, как и в случае беззнаковых чисел, коды этих чисел начинаются с 0 (см. диапазон). Соответственно, коды отрицательных чисел начинаются с 1. Множество отрицательных чисел так же, как и множество положительных, представляется множеством двоичных кодов, упорядоченных по возрастанию.
. Неотрицательные числа кодируются так же, как и в случае беззнаковых чисел, коды этих чисел начинаются с 0 (см. диапазон). Соответственно, коды отрицательных чисел начинаются с 1. Множество отрицательных чисел так же, как и множество положительных, представляется множеством двоичных кодов, упорядоченных по возрастанию.
Рассмотрим, например, тип данных, в котором для кодирования целых чисел со знаком используется 2 разряда. В нем могут быть закодированы числа - 2, - 1, 0, 1 с помощью кодов 10, 11, 00, 01, соответственно. Если тип данных содержит 3 разряда, то в нем могут быть представлены числа - 4, - 3, - 2, - 1, 0, 1, 2, 3 соответственно с помощью кодов 100, 101, 110, 111, 000, 001, 010, 011.
В общем случае левая граница диапазона кодируется двоичным словом 100\dots0, а правая - двоичным словом 011\dots1.
Итак, если двоичный код числа начинается с 1, то он представляет отрицательное целое число, а если с 0, - то неотрицательное. Старший разряд двоичного кода называется знаковым разрядом. Код, который используется для кодирования неотрицательных целых чисел, называется прямым, а для кодирования отрицательных - дополнительным. Дополнительные коды позволяют заменить операцию вычитания операцией сложения и сделать возможной реализацию операций сложения и вычитания одинаковыми для знаковых и беззнаковых чисел (см. ниже).
Рассмотрим понятия прямого и дополнительного кода в общем случае для системы счисления с основанием p, где p - целое, p> 1.
Пусть для p-ичного кодирования , т. е. для представления целого числа в системе счисления с основанием p, используется k разрядов, и диапазон кодируемых чисел составляет от 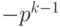 до
до 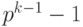 .
.
Для целого числа x, такого что 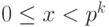 , выполняется разложение
, выполняется разложение
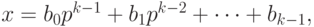
где 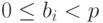 , для i = 0, 1, \dots, k - 1.
, для i = 0, 1, \dots, k - 1.
Прямым кодом числа x называется его представление в p-ичном виде с помощью слова длины k:
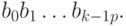
Обратным кодом числа (-x) называется код
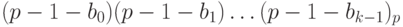
Обозначим через 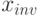 число, которое представляет этот код. Имеем:
число, которое представляет этот код. Имеем:
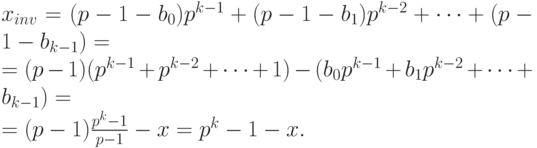
Дополнительным кодом отрицательного числа (- x) называется p-ичное представление положительного числа
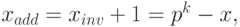
или p-ичное представление суммы
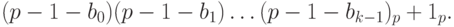
Отсюда, в частности, следует, что  и
и 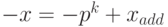 .
.
Например, найдем дополнительный код числа 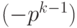 - левой границы диапазона. Прямой код числа
- левой границы диапазона. Прямой код числа 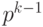 равен
равен 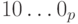 . Поэтому обратный код числа -
. Поэтому обратный код числа - 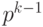 имеет вид:
имеет вид: 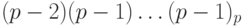 . Соответственно, дополнительный код выглядит следующим образом:
. Соответственно, дополнительный код выглядит следующим образом:
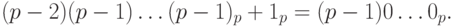
Аналогично, найдем дополнительный код числа (- 1). Число 1 имеет прямой код 00\dots1, следовательно, обратный код для (- 1) имеет вид: 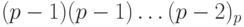 . Поэтому дополнительным кодом числа (- 1) является
. Поэтому дополнительным кодом числа (- 1) является 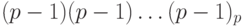 . Найдем также дополнительный код числа 0. Это число имеет прямой код
. Найдем также дополнительный код числа 0. Это число имеет прямой код  и, соответственно, обратный код
и, соответственно, обратный код 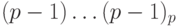 . Следовательно, дополнительный код равен 1
. Следовательно, дополнительный код равен 1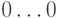 , так что
, так что 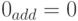 . Отметим, что в k-разрядной целочисленной арифметике полагают
. Отметим, что в k-разрядной целочисленной арифметике полагают 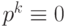 , т. е. все числа рассматриваются как остатки от деления на
, т. е. все числа рассматриваются как остатки от деления на 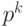 .
.
Пример 2. Найдем дополнительный код числа (- 127) при двоичном кодировании в 1 байте. Имеем:
прямой код числа 127: 01111111;
обратный код: 10000000;
дополнительный код: 10000000 + 1 = 10000001;
Пример 3. Найдем дополнительный код числа (- 12) при двоичном кодировании в 4 байтах типа данных integer. Имеем:
прямой код числа 12: 00000000 00000000 00000000 00001100;
обратный код: 11111111 11111111 11111111 11110011;
дополнительный код: 11111111 11111111 11111111 11110100,
или fffffff4 (hex).
Пример 4. Пусть p = 10. Тогда с помощью 4 разрядов можно закодировать целые числа в пределах от 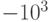 до
до 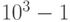 , т. е. от - 1000 до 999. Найдем дополнительный код при десятичном кодировании числа (- 812). Имеем:
, т. е. от - 1000 до 999. Найдем дополнительный код при десятичном кодировании числа (- 812). Имеем:
прямой код для 812: 0812;
обратный код: 9187;
дополнительный код: 9188 (= 10000 - 812).
Пример 5. Пусть p = 16. Тогда с помощью 3 разрядов можно закодировать числа в пределах от - 256 до 255. Найдем дополнительный код при 16-ричном кодировании числа (- 50). Имеем:
прямой код числа 50: 032;
обратный код: fcd;
дополнительный код: fce.
