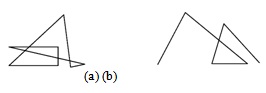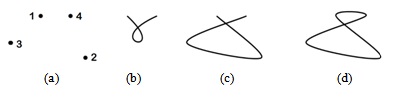Представление графической информации
Рассмотрим также примеры других видов графики - пиксельную и символьную.
В пиксельной графике изображение строится на уровне пикселей в растровом редакторе с малым разрешением. Эта графика используется для создания компьютерных игр на устройствах с малым разрешением экрана (рис. 3.9 (a)).
В символьной графике изображение создается в текстовой форме из набора символов таблицы ASCII (рис. 3.9 (b)). Сначала подобные изображения создавались на печатных машинках, затем с помощью программ на ЭВМ. Данное направление называется ASCII-артом. Расширением ASCII-графики является ANSI-графика, в которой для создания изображения используются 224 печатных символа и цвет.
Пример 15. Ниже приведен ASCII-рисунок и 16-ричные коды символов каждой строки (см. табл. 2.6):
(\___/) 28 5c 5f 5f 5f 2f 29
(=' . '=) 28 3d 27 20 2e 20 27 3d 29
(") _ (") 28 22 29 20 5f 20 28 22 29
Графические примитивы. Кривые Безье
Ниже рассматриваются некоторые способы представления основных графических примитивов в языках программирования, обсуждаются понятия кривой Безье и B-сплайна, приводятся примеры их построения.
Примитивы - набор графических объектов, с помощью которого конструируются другие, более сложные графические объекты.
Основные графические примитивы
В клиентской области окна используется прямоугольная система координат, начало координат которой находится в левом верхнем углу, ось абсцисс направлена вправо, ось ординат - вниз, единицей измерения является пиксель (рис. 3.10). Ниже приведены примеры представления геометрических объек
-
Точка (point) представляется двумя координатами (x, y).
- Отрезок (line) определяется двумя точками - его концами.
-
Прямоугольник (rectangle) может представляться
- координатами противоположных вершин ( рис. 3.11 (a)), правой верхней и левой нижней или наоборот;
-
координатами левой верхней вершины, а также шириной (width) и высотой (height) прямоугольника (рис. 3.11 (b)).

Рис. 3.11. Представление прямоугольника и эллипса: (a) противоположными вершинами; (b) левой верхней вершиной, шириной и высотой; (c) описанным прямоугольникомШириной прямоугольника называется длина его горизонтальной стороны, а высотой - длина вертикальной.
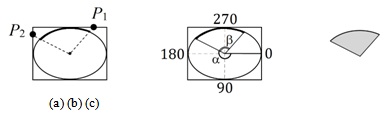
- Эллипс (ellipse) определяется описанным прямоугольником (рис. 3.11 (c)), иногда - центром и осями.
-
Дуга (arc) и сектор (pie) эллипса рис. 3.12 представляются прямоугольником, описанным вокруг эллипса (см. выше п. 3), а также следующими двумя параметрами:
- двумя точками на границе прямоугольника: дуга (сектор) эллипса заключается между лучами, которые соединяют центр прямоугольника и эти точки, в направлении против часовой стрелки ( рис. 3.12 (a));
-
величиной начального угла (
 ) и угла раствора дуги (
) и угла раствора дуги ( ) в градусах; начальный угол откладывается от точки касания эллипса правой стороны прямоугольника; углы откладываются в направлении по часовой стрелке (рис. 3.12 (b)).
) в градусах; начальный угол откладывается от точки касания эллипса правой стороны прямоугольника; углы откладываются в направлении по часовой стрелке (рис. 3.12 (b)).
-
Многоугольник (polygon) и ломаная (polyline) представляются массивом (списком) точек (рис. 3.13).
-
Скругленный прямоугольник (rounded rectangle), или прямоугольник с закругленными углами, определяется параметрами прямоугольника (см. выше), а также шириной и высотой эллипса (рис. 3.14 (a)), который используется для "скругления" (рис. 3.14 (b)): вместо угла отображается дуга эллипса - его четвертая часть (рис. 3.14 (c)).
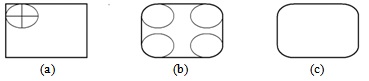
Рис. 3.14. Скругление прямоугольника: (a) эллипс; (b) скругление; (c) прямоугольник с закругленными угламиШириной эллипса называется длина его горизонтальной оси, а высотой - длина вертикальной оси.
Максимальное закругление прямоугольника достигается, когда ширина и высота прямоугольника совпадают с шириной и высотой эллипса. В этом случае скругленный прямоугольник совпадает с эллипсом.
- Кривые Безье (Bezier curve) и сплайны (spline) представляются массивами (списками) точек (см. ниже). На рис. 3.15 показаны 4 точки (рис. 3.15 (a)) и построенные по ним кривая Безье (рис. 3.15 (b)), сплайн (curve) (рис. 3.15 (c)) и замкнутый сплайн (closed curve) (рис. 3.15 (d)).