Предсказание рисков и рейтингование
Сравнительный анализ финансового состояния фирм
Сравнительный анализ, в отличие от рейтингования, предполагает введение не одной, а нескольких оценочных координат. Это позволяет лучше использовать имеющуюся информацию, более точно позиционировать фирму среди остальных. С другой стороны, для обозримости результатов сравнительного анализа, количество параметров сравнения должно быть по возможности минимальным. В узком смысле "обозримость" требует введения не более двух координат - чтобы относительная позиция фирмы могла быть представлена точкой на двумерной карте, а различные финансовые показатели могли быть визуализированы в виде двумерных поверхностей.
Постановка задачи
С математической точки зрения эта задача сводится к оптимальному сжатию информации о финансовом состоянии фирмы, т.е. отображении информации минимальным числом параметров при заданном уровне огрубления или минимизации потерь информации при заданном числе обобщенных координат. Для целей визуализации, выгодно ограничиться двухпараметрическим представлением. Это уже существенный шаг вперед по сравнению с однопараметрическим рейтингом.
Данные о российских банках
Для иллюстрации описываемого подхода далее в этой лекции 5Наше изложение будет следовать работе (Shumsky, Yarovoy, 1998), выполненной по заказу и при финансовой поддержке агентства "Прайм". будут использованы данные Центрального Банка России о годовых балансах и отчетах о прибылях/убытках примерно 1800 российских банков за 1994, 1995 годы, предоставленные информационным агентством "Прайм". Каждый банк при этом описывается 30 финансовыми показателями - отношением балансовых статей к общей сумме активов банка. Подобная нормализация приводит все статьи к единому масштабу, сглаживая различия между крупными и мелкими банками, составляющие несколько порядков величин. Из этих 30 параметров нам предстоит оптимальным образом сконструировать две обобщенные координаты.
Сечения
Главный вопрос теперь - как выбирать эти обобщенные координаты. Можно, например, воспользоваться сечениями имеющихся многомерных данных, иными словами - просто выбрать два "наиболее важных" с точки зрения экспертов параметра балансов и таким образом отобразить на двумерной карте положение всех фирм. Для российских банков подобное представление информации практикует журнал "Эксперт" (см рисунок 10.2).
Рис. 10.2. Положение пятнадцати крупнейших российских банков в 1996 г. в координатах "Надежность" - Доходность. (По материалам журнала "Эксперт")
Согласно такому подходу надежность банка характеризуется одним финансовым показателем - отношением собственного капитала к привлеченному. В первой половине этой лекции мы видели, однако, что анализ банкротств выявляет как минимум пять (а то и восемь) значимых финансовых показателей, влияющих на надежность.
Линейное сжатие информации - метод главных компонент
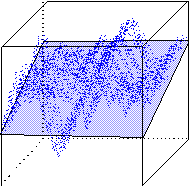
Более общий подход - использовать не две отдельные компоненты, а две линейные комбинации всех 30 исходных параметров, наилучшим образом представляющие имеющиеся данные (см. рисунок 10.3).
Каждый банк представлен точкой в 30-мерном пространстве и задача состоит в проведении двумерной плоскости в этом пространстве, обеспечивающей минимальное среднеквадратичное отклонение имеющихся точек от этой плоскости:
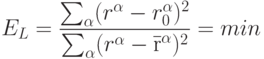
Как мы знаем подобное линейное приближение дается методом главных компонент. Если действительное расположение точек не сильно
отклоняется от плоскости, этот метод может дать неплохое начальное приближение. Однако, оказывается, что в даном случае это не так.
Среднеквадратичное отклонение для случая двух главных компонент оказалось равным почти половине от общей дисперсии: 
.
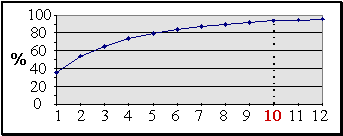
Таким образом, даже оптимальный вариант линейного сжатия не дает возможности визуализировать финансовое положение банков. Оно может, тем не менее, оказаться полезным, в частности, для анализа значимости балансовых статей. Так, увеличение числа главных компонент постепенно дает все лучшее и лучшее приближение имеющегося массива данных.
Например, 10 главных компонент обеспечивают вполне приемлемую общую точность 94% (т.е. 
). При общем числе входов равном 30,
это означает 3-кратное сжатие информации. Такое сжатие оказывается возможным из-за существенных корреляций между отдельными статьями в
балансовой отчетности. При этом те статьи, которые дают наибольший вклад в главные компоненты, восстанавливаются по ним с наибольшей
точностью.
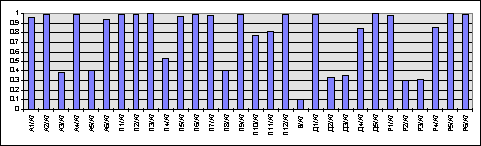
Степень восстановления исходных данных по ограниченному числу главных компонент свидетельствует о том, насколько согласованны данные в этих статьях между собой во всем массиве имеющейся информации, т.е. насколько содержащаяся в них информация значима для выявления индивидуальных отличий показывает, что около 20 статей восстанавливаются по 10 главным компонентам с относительно высокой точностью. Это как раз те статьи, кторые дают основной вклад в главные компоненты. Остальные статьи гораздо менее значимы для сравнительного финансового анализа, в частности, в силу незначительности совокупной доли активов в этих статьях балансов.
