Извлечение знаний с помощью нейронных сетей

Исправление данных

Итак, перед извлечением правил из нейронной сети производится ее обучение и прореживание. Упомянем еще об одной процедуре, которая иногда осуществляется при извлечении знаний из нейронных сетей - исправление (очищение). Подобная операция была предложена Вайгендом и коллегами и по сути используется параллельно с обучением (Weigend, Zimmermann, & Neuneier 1996). Гибридное использование обучения и исправления данных носит название CLEARNING (CLEARING+LEARNING). Данная процедура включает восходящий процесс обучения, при котором данные изменяют связи в нейронной сети и нисходящий процесс, в котором нейронная сеть изменяет данные, на которых производится обучение. Ее достоинствами являются выявление и удаление информационных записей, выпадающих из общей структуры обучающей выборки, а также замена искаженных данных и данных с лакунами на исправленные величины. При использовании данной процедуры происходит торг между доверием к данным и доверием к нейросетевой модели, обучаемой на этих данных. Эта конкуренция составляет существо так называемой дилеммы наблюдателя и наблюдений.

Способность работать с неточными данными является одним из главных достоинств нейронных сетей. Но она же парадоксальным образом является и их недостатком. Действительно, если данные не точны, то сеть в силу своей гибкости и адаптируемости будет подстраиваться к ним, ухудшая свои свойства обобщения. Эта ситуация особенно важна при работе с финансовыми данными. В последнем случае существует множество источников погрешности. Это и ошибки при вводе числовых значений или неправильная оценка времени действия ценных бумаг (например, они уже не продаются). Кроме того, если даже данные и введены правильно, они могут быть слабыми индикаторами основополагающих экономических процессов, таких как промышленное производство или занятость. Наконец, возможно, что многие важные параметры не учитываются при обучении сети, что эффективно может рассматриваться как введение дополнительного шума. Данные, далеко выпадающие из общей тенденции, забирают ресурсы нейронной сети. Некоторые из нейронов скрытого слоя могут настраиваться на них. При этом ресурсов для описания регулярных слабо зашумленных областей может и не хватить. Множество попыток применения нейронных сетей к решению финансовых задач выявило важное обстоятельство: контроль гибкости нейросетевой модели является центральной проблемой. Изложим кратко существо процедуры обучения сети, объединенной с исправлением данных. Для простоты рассмотрим сеть с одним входом и одним выходом. В этом случае минимизируемой величиной является сумма двух слагаемых (Weigend & Zimmermann, 1996):

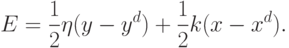
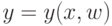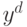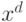Первый член описывает обычно минимизируемое в методе обратного распространения ошибки квадратичное отклонение выхода нейронной сети от желаемого значения . Второе слагаемое представляет собой квадратичное отклонение исправленного входного значения от реального его значения . Соответственно, для весов сети и для исправленных входных значений получаются два правила их модификации. Для весов оно такое же, как и в стандартном методе обратного распространения ошибки, а для исправленного входа имеет вид

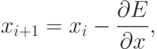
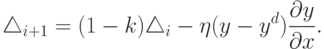
Это уравнение включает

• экспоненциальное затухание : в отсутствие нового входа стремится к нулю со скоростью пропорциональной .
• член, пропорциональный ошибке выходного значения 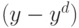: аналогичная пропорциональность свойственна и обычному соотношению для модификации весов - чем больше ошибка, тем больше ее влияние на исправление входного значения. Этот член также пропорционален чувствительности выхода ко входу - .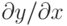

Вайгенд и его коллеги предложили наглядную механическую интерпретацию минимизируемой функции, а также отношению скоростей обучения и исправления (см. рисунок 9.4).

Рис. 9.4.

При обычном обучении (без исправления входного вектора) данные располагаются в пространстве вход-выход. Наблюдаемое выходное значение состояния выходного нейрона может рассматриваться как поверхность над пространством входов. Точки, изображающие данные обучающего набора вертикально прижимаются к этой поверхности пружинами, которые запасают некоторую энергию сжатия. Сложность нейронной сети определяется в конкуренции между жесткостью поверхности и жесткостью пружин. В одном из предельных случаев, бесконечно мягкая сеть (поверхность) пройдет как раз через все точки, определяемые данными. В противоположном случае, чрезмерно эластичные пружины не будут оказывать воздействия на поверхность и менять нейронную сеть.

Введение механизма исправления данных соответствует добавлению пружин в пространстве входов - между каждой точкой данных 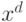и исправленным значением . Энергия, запасенная в этих пружинах составляет 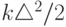. Минимизация суммарной функции ошибки соответствует минимизации полной энергии, запасенной в обеих типах пружин. Отношение описывает конкуренцию между важностью ошибок выхода и важностью ошибок входа.