Предсказание финансовых временных рядов
Метод искусственных примеров (hints)
Одним из самых "больных мест" в финансовых предсказаниях является дефицит примеров для обучения нейросети. Финансовые рынки, вообще говоря, не стационарны (особенно российские). Появляются новые финансовые инструменты, для которых еще не накоплена история, изменяется характер торговли на прежних рынках. В этих условиях длина доступных для обучения нейросети временных рядов весьма ограничена.
Однако, можно повысить число примеров, используя для этого те или иные априорные соображения об инвариантах динамики временного ряда. Это еще одно физико-математическое понятие, способное значительно улучшить качество финансовых предсказаний. Речь идет о генерации искусственных примеров, получаемых из уже имеющихся применением к ним различного рода преобразований.
Поясним основную мысль на примере. Психологически оправдано следующее предположение: игроки обращают внимание, в основном, на форму кривой цен, а не на конкретные значения по осям. Поэтому если немного растянуть по оси котировок весь временной ряд, то полученный в результате такого преобразования ряд также можно использовать для обучения наряду с исходным. Мы, таким образом, удвоили число примеров за счет использования априорной информации, вытекающей из психологических особенностей восприятия временных рядов участниками рынка6Естественно, таким образом можно не только удвоить число примеров, но и учетверить их и т.д. Более того, мы не просто увеличили число примеров, но и ограничили класс функций, среди которых ищется решение, что также повышает качество предсказаний (если, конечно, использованный инвариант соответствует действительности).
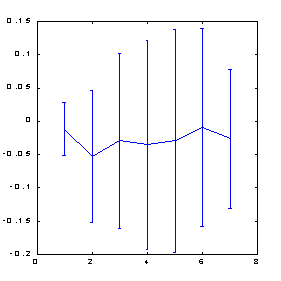
Приведенные ниже результаты вычисления предсказуемости индекса S&P500 методом box-counting (см. рисунки 8.7, 8.8) иллюстрируют роль искусственных примеров. Пространство признаков в данном случае формировалось методом ортогонализации, описанным в лекции о способах предобработки данных. В качестве входных переменных использовались 30 главных компонент в 100-мерном лаговом пространстве. Из этих главных компонент были выбраны 7 признаков - наиболее значимые ортогональные линейные комбинации. Как видно из этих рисунков, лишь применение искусственных примеров оказалось способным в данном случае обеспечить заметную предсказуемость.
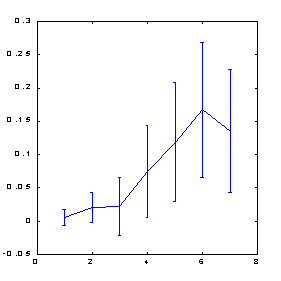
Рис. 8.8. Предсказуемость знака изменения котировок индекса S&P500 после учетверения числа примеров методом растяжения по оси цен
Обратите внимание, что использование ортогонального пространства признаков привело к некоторому повышению предсказуемости по сравнению с обычным способом погружения: с 0.12 бит ( рисунок 8.5) до 0.17 бит (рисунок 8.8). Чуть позже, когда пойдет речь о влиянии предсказуемости на прибыль, мы покажем, что за счет этого норма прибыли может увеличиться почти в полтора раза.
Другой, менее тривиальный, пример удачного использования такого рода подсказок (hints) для нейросети в каком направлении искать
решение - использование скрытой симметрии в валютной торговле. Смысл этой симметрии в том, что валютные котировки могут рассмматриваться
с двух "точек зрения", например как ряд DM/$ или как ряд $/DM. Возрастание одного из них соответствует уменьшению другого.
Это свойство можно использовать для удвоения числа примеров: каждому примеру вида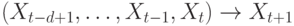 
можно добавить его симметричный аналог 
.
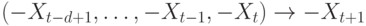Эксперименты по нейросетевому предсказанию показали, что для основных валютных рынков учет симметрии поднимает норму прибыли
примерно в два раза, конкретно - с 5% годовых до 10% годовых, с учетом реальных транзакционных издержек (Abu-Mostafa, 1995).