|
как начать заново проходить курс, если уже пройдено несколько лекций со сданными тестами? |
Эллиптические кривые
4.1 Эллиптические кривые
4.1.1 Определения
За подробными сведениями об эллиптических кривых отправляем читателя к [1], [2]. Ниже мы будем рассматривать материал, необходимый для решения типовых расчетных задач.
Предположим, что 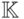 - поле: либо поле
- поле: либо поле  вещественных чисел, либо поле
вещественных чисел, либо поле  рациональных чисел, либо поле
рациональных чисел, либо поле 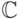 комплексных чисел, либо поле
комплексных чисел, либо поле  из
из 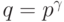 элементов,
элементов,  - простое (см. ниже пример кривой над
- простое (см. ниже пример кривой над 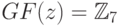 . Напомним, что характеристикой поля
. Напомним, что характеристикой поля 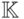 называется наименьшее такое натуральное число
называется наименьшее такое натуральное число 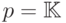 , что
, что 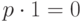 , где 1 и 0 - единичный и нулевой элементы
, где 1 и 0 - единичный и нулевой элементы 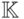 соответственно.
соответственно.
Определение 4.1 Алгебраической кривой порядка  над полем
над полем 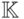 называется множество пар
называется множество пар 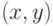 ,
, 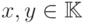 , удовлетворяющих уравнению
, удовлетворяющих уравнению 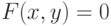 , где
, где 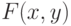 - многочлен степени
- многочлен степени  с коэффициентами из
с коэффициентами из 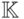 .
.
Напомним, что степенью одночлена называется сумма степеней входящих в него переменных, а степенью многочлена - максимальная из степеней составляющих его одночленов.
Пример 4.1 Степень одночлена 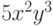 равна
равна 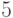 , а степень многочлена
, а степень многочлена 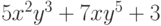 равна
равна 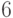 .
.
Определение 4.2 Пары 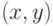 элементов поля
элементов поля 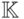 , удовлетворяющие уравнению кривой, называются ее точками.
, удовлетворяющие уравнению кривой, называются ее точками.
Определение 4.3 Точка 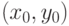 кривой
кривой 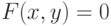 называется неособой, если значения частных производных многочлена
называется неособой, если значения частных производных многочлена  в ней не равны нулю одновременно.
в ней не равны нулю одновременно.
Частные производные 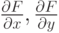 определяются известными формальными правилами дифференцирования, применяемыми к многочленам над произвольным полем (линейность дифференцирования и правило Лейбница), из которых следует: если многочлен
определяются известными формальными правилами дифференцирования, применяемыми к многочленам над произвольным полем (линейность дифференцирования и правило Лейбница), из которых следует: если многочлен 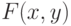 записан по степеням
записан по степеням  :
:
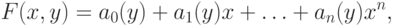
то
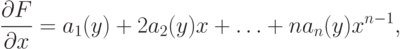
и аналогичная формула имеет место для частного дифференцирования по переменной  .
.
Определение 4.4 Кривая называется неособой, или гладкой, если все её точки неособые. В любой такой точке 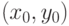 к ней можно провести касательную, т. е. прямую, определяемую уравнением
к ней можно провести касательную, т. е. прямую, определяемую уравнением
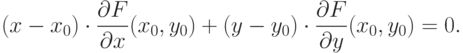
Определение 4.5 Гладкая кривая третьего порядка над полем 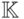 называется эллиптической кривой над тем же полем, если на ней есть хотя бы одна точка.
называется эллиптической кривой над тем же полем, если на ней есть хотя бы одна точка.
Но если даже точек нет, то они могут появиться, если рассмотреть эту кривую над каким-нибудь расширением поля 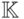 .
.
Будем также считать принадлежащей эллиптической кривой бесконечно удаленную точку 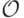 , являющейся точкой перересечения эллиптической кривой и любой вертикальной прямой.
, являющейся точкой перересечения эллиптической кривой и любой вертикальной прямой.
Произвольную эллиптическую кривую над полем 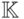 можно преобразовать заменой переменных к виду:
можно преобразовать заменой переменных к виду:
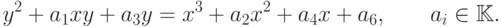 |
( 4.1) |
Если характеристика основного поля не равна 2 или 3, то это уравнение можно преобразовать к виду:
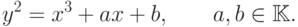 |
( 4.2) |
Теорема 4.1 Кривая 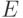 , заданная уравнением (4.2), является гладкой тогда и только тогда, когда
, заданная уравнением (4.2), является гладкой тогда и только тогда, когда
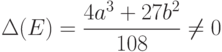 |
( 4.3) |
Выражение 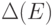 является дискриминантом многочлена
является дискриминантом многочлена 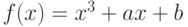 , и равно нулю тогда и только тогда, когда этот многочлен имеет кратные корни.
, и равно нулю тогда и только тогда, когда этот многочлен имеет кратные корни.
