|
как начать заново проходить курс, если уже пройдено несколько лекций со сданными тестами? |
Алгебраические системы
3.2 Индексы
Пусть 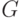 - группа,
- группа,  - её элемент,
- её элемент, 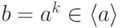 . Число
. Число  называется дискретным логарифмом элемента
называется дискретным логарифмом элемента  по основанию
по основанию  (пишут
(пишут  ). В случае, когда
). В случае, когда  - примитивный корень по модулю
- примитивный корень по модулю  , дискретный логарифм
, дискретный логарифм  ещё называют индексом числа
ещё называют индексом числа  по модулю
по модулю  при основании
при основании  . Пишут:
. Пишут:  . Когда примитивный корень
. Когда примитивный корень  фиксирован, можно также писать:
фиксирован, можно также писать: 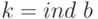 .
.
Дискретное логарифмирование в произвольной группе является трудноразрешимой задачей. Приведём один из примеров, когда оно всё-таки легко осуществимо.
Пример 3.7 Вычислить дискретный логарифм числа 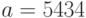 по основанию
по основанию 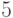 по модулю
по модулю  .
.
Решение. Порядок мультипликативной группы поля вычетов по модулю 102673 равен 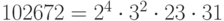 . Число, являющееся произведением большого количества небольших чисел, называется гладким. Для дискретного логарифмирования в таком поле существует алгоритм Полига-Хэллмана, который мы сейчас применим.
. Число, являющееся произведением большого количества небольших чисел, называется гладким. Для дискретного логарифмирования в таком поле существует алгоритм Полига-Хэллмана, который мы сейчас применим.
Если  - решение нашей задачи, и
- решение нашей задачи, и  ,
, 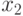 ,
, 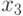 ,
, 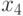 - остатки от деления
- остатки от деления  на
на 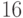 ,
, 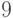 ,
, 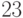 и
и  соответственно, то
соответственно, то

где
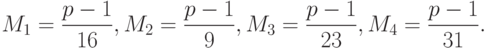
Наоборот, если мы найдём  ,
, 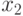 ,
, 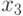 и
и 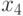 , а решение
, а решение  задачи всегда существует (так как
задачи всегда существует (так как 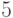 - примитивный корень), то
- примитивный корень), то  будет совпадать с единственным решением
будет совпадать с единственным решением 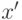 системы:
системы:
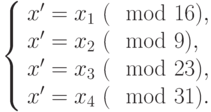
Итак, для решения задачи, по китайской теореме об остатках нужно найти:
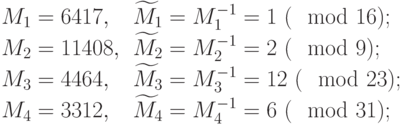
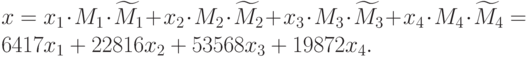
Следовательно, нам нужно найти  ,
, 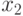 ,
, 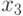 ,
, 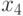 .
.
Имеем:
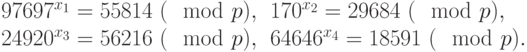
Поскольку порядок группы  равен 23, а группы
равен 23, а группы 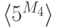 - всего 31, то при различных
- всего 31, то при различных 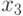 ,
, 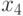 величины
величины  и
и  пробегают, соответственно, по 23 и 31 различным значениям.
пробегают, соответственно, по 23 и 31 различным значениям.
Тогда 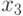 и
и 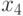 можно найти полным перебором, проверив
можно найти полным перебором, проверив 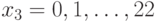 ,
,  . В нашем случае
. В нашем случае 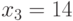 ,
,  . Числа
. Числа 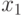 и
и 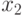 также можно искать полным перебором, но для них можно ещё уменьшить количество попыток. Будем искать
также можно искать полным перебором, но для них можно ещё уменьшить количество попыток. Будем искать
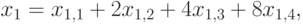
где 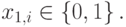
Имеем:
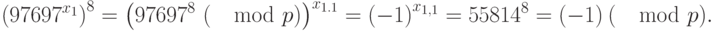
То есть 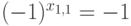 . Отсюда
. Отсюда 
Далее,

Проверим оба варианта  :
:


Отсюда 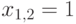 .
.
Далее,
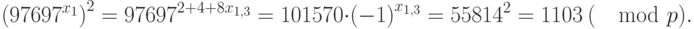
Опять, из двух вариантов выбираем верный: 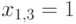 .
.
Наконец,
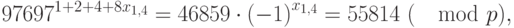
откуда 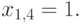 Проверяем:
Проверяем:
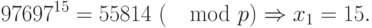
Аналогично находим  .
.
По китайской теореме об остатках находим  .
.
Для небольших  бывает удобно вычислять все степени примитивного корня и строить на основе этих вычислений две таблицы, называемые таблицами индексов. Таблицы индексов используются для быстрого решения некоторых задач по модулю простого числа
бывает удобно вычислять все степени примитивного корня и строить на основе этих вычислений две таблицы, называемые таблицами индексов. Таблицы индексов используются для быстрого решения некоторых задач по модулю простого числа  .
.
Приведем эти таблицы для примитивного корня 2 по модулю 37:
Например, чтобы определить индекс по числу 13, нужно в первой таблице перейти к столбцу "1" и строке "3". Итак, 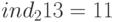 . Наоборот, для нахождения числа по его индексу 11 нужно во второй таблице перейти в столбец "1" строку "1". Имеем:
. Наоборот, для нахождения числа по его индексу 11 нужно во второй таблице перейти в столбец "1" строку "1". Имеем: 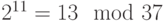 .
.
Пример 3.8 Решим с помощью таблицы индексов сравнение:
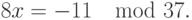
Будем далее использовать примитивный корень 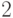 и построенные для него выше таблицы. Правую часть сравнения заменяем положительным вычетом:
и построенные для него выше таблицы. Правую часть сравнения заменяем положительным вычетом:

"Индексируем" левую и правую части сравнения:

Находим в первой таблице для простого числа 37 значение 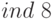 и
и 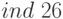 и подставляем в сравнение. Получим:
и подставляем в сравнение. Получим:
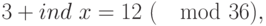
Откуда
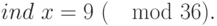
По второй таблице находим число, соответствующее индексу 9. Получим: 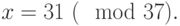
Пример 3.9 С помощью индексов решить сравнение:
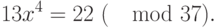
Индексируем сравнение:
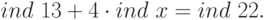
По первой таблице индексов находим:  ,
,  . Отсюда:
. Отсюда:  , или
, или 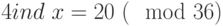 . Последнему сравнению удовлетворяют
. Последнему сравнению удовлетворяют  . Для каждого из них по второй таблице индексов найдем
. Для каждого из них по второй таблице индексов найдем 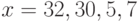 .
.
