Виды графов и их свойства

Программа 17.15. Символьная индексация имен вершин

Данная реализация индексации строковых ключей с помощью символов (описанной в пояснении к программе 17.14) завершает эту задачу, добавляя поле index в каждый узел TST-дерева (см. программу 15.8). Индекс, связанный с каждым ключом, хранится в поле индекса узла, соответствующего символу конца строки этого ключа.

Как обычно, мы используем символы ключа поиска для спуска по TST-дереву. При достижении конца ключа мы, если нужно, устанавливаем значение его индекса, а также устанавливаем значение приватного члена данных val, которое возвращается вызывающей функции после возврата из всех рекурсивных вызовов.

  #include <string>
  class ST
    { int N, val;
      struct node
        { int v, d; node* l, *m, *r;
          node(int d) : v(-1), d(d), l(0), m(0), r(0) {}
        } ;
      typedef node* link;
      link head;
      link indexR(link h, const string &s, int w)
        { int i = s[w];
          if (h == 0) h = new node(i);
          if (i == 0)
            { if (h->v == -1) h->v = N++;
              val = h->v;
              return h;
            }
          if (i < h->d) h->l = indexR(h->l, s, w);
          if (i == h->d) h->m = indexR(h->m, s, w+1);
          if (i > h->d) h->r = indexR(h->r, s, w);
          return h;
        }
    public:
      ST() : head(0), N(0) { }
      int index(const string &key)
        { head = indexR(head, key, 0); return val; }
    } ;
      

В основе некоторых графов лежат неявные связи между их элементами. Мы не будем рассматривать такие графы, а просто покажем несколько примеров и посвятим им несколько упражнений. Если нам понадобится обработать такой граф, то, конечно, можно написать программу построения явного графа, перебрав все его ребра, однако существуют задачи, решение которых не требует просмотра всех ребер, благодаря чему их можно решить за сублинейное время.

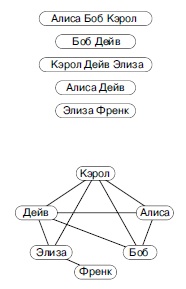
Граф со степенями разделения. Рассмотрим некоторую совокупность подмножеств из V элементов и определим граф следующим образом: каждому элементу объединения подмножеств соответствует одна вершина, а ребро между двумя вершинами существует в том случае, если обе вершины принадлежат одному подмножеству (см. рис. 17.15). Это может быть и мультиграф, в котором ребра помечены именами соответствующих подмножеств. Говорят, что все элементы, инцидентные данному элементу v, отделены от него одной степенью разделения (degree of separation). Иначе все элементы, инцидентные какому-либо элементу, который отделен i степенями разделения от вершины v (о которых еще не известно, сколькими степенями разделения они отделены от вершины v —i или меньше), отделены i + 1 степенями разделения от вершины v. Это построение развлекало многих людей, от математиков (числа Эрдеша (Erdos)) до любителей кинофильмов ( " шесть шагов до Кевина Бэкона " ).

Рис. 17.15. Граф со степенями разделения

Граф в нижней части рисунка определяется группами, показанными в верхней части: каждому имени соответствует вершина, а ребра соединяют вершины с именами, попадающими в одну и ту же группу. Кратчайшие длины путей в графе соответствуют степеням разделения. Например, Фрэнк отделен от Алисы и Боба тремя степенями разделения.

Интервальный граф. Пусть имеется совокупность V интервалов на действительной оси (заданных парами вещественных чисел). Граф определяется следующим образом: каждому интервалу ставится в соответствие вершина, а ребра между вершинами проводятся в том случае, когда соответствующие интервалы пересекаются (имеют хотя бы одну общую точку).

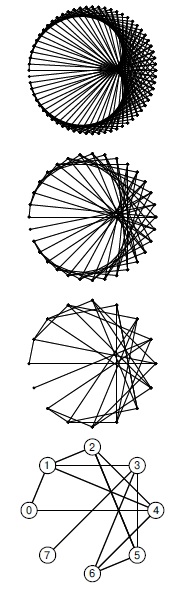
Граф де Брюйна. Предположим, что V равно степени 2. Мы определяем орграф следующим образом: каждому неотрицательному целому числу, меньшему V, соответствует одна вершина графа, а ребра соединяют каждую вершину i с вершинами 2i mod V и (2i + 1) mod V. Эти графы удобны для изучения последовательностей значений, которые возникают в сдвиговых регистрах фиксированной длины при выполнении последовательностей сдвигов всех разрядов на одну позицию влево, когда самый левый разряд отбрасывается, а самый правый разряд заполняется нулем или единицей. На рис. 17.16 изображены графы де Брюйна (de Bruijn) с 8, 16, 32 и 64 вершинами.

Рис. 17.16. Графы де Брюйна

Орграф де Брюйна порядка n содержит 2ⁿ вершин и ребра, соединяющие вершины i с вершинами 2i mod 2ⁿ и (2i + 1) mod 2ⁿ для всех i . Здесь показаны неориентированные графы, соответствующие орграфам де Брюйна порядка 6, 5, 4 и 3 (сверху вниз).

Различные виды графов, описанные в этом разделе, обладают различными характеристиками. Однако для наших программ они все одинаковы: это просто множества ребер. Как мы уже убедились в главе 1 "Введение" , определение даже простейших свойств графов может оказаться сложной вычислительной проблемой. В этой книге будут описаны различные хитроумные алгоритмы, которые разработаны для решения практических задач, связанных со многими видами графов.

Примеры, приведенные выше в данном разделе, показывают, что графы -это сложные комбинаторные объекты, намного сложнее лежащих в основе других алгоритмов, которые были рассмотрены в частях I—IV. Во многих случаях графы, которые приходится обрабатывать в приложениях, трудно или даже невозможно как-то охарактеризовать. Алгоритмы, которые хорошо работают на случайных графах, часто неприменимы к реальным ситуациям ввиду того, что зачастую трудно генерировать случайные графы с такими же структурными характеристиками, что и реальные графы. Обычно в таких ситуациях разрабатываются алгоритмы, которые хорошо работают в худшем случае. Этот подход годится в одних случаях, но не оправдывает ожиданий в других (в силу своей консервативности).

Изучение производительности алгоритмов на графах, сгенерированных на базе одной из рассмотренных вероятностных моделей, не всегда дает достаточно точную информацию для предсказания производительности на реальных графах. Однако генераторы графов, которые были рассмотрены в данном разделе, удобны для тестирования реализаций и предварительной оценки производительности алгоритмов. Прежде чем прогнозировать производительность приложения, необходимо хотя бы проверить правильность всех предположений о взаимоотношениях между различными данными приложения со всеми используемыми моделями или выборками. Такая проверка целесообразна при работе в любой прикладной области и уж тем более важна при обработке графов в силу большого разнообразия возможных видов графов.

Упражнения

17.61. Какую часть генерируемых ребер составляют петли, если для построения случайных графов с насыщенностью aV используется программа 17.12?

17.62. Вычислите ожидаемое количество полученных параллельных ребер, если для генерации случайных графов с V вершинами и насыщенностью а используется программа 17.12. Воспользуйтесь полученным результатом для построения графиков зависимости доли параллельных ребер от a при V= 10, 100 и 1000.

17.63. Воспользуйтесь контейнером map из библиотеки STL для разработки альтернативной реализации класса ST из программы 17.15.

17.64. Найдите в интернете большой неориентированный граф -возможно, данные о связности узлов сети, либо граф разделения, определенный соавторами из библиографического списка или актерами из списка кинофильмов.

17.65. Напишите программу, которая генерирует разреженные случайные графы для специально подобранных наборов значений V и E и выводит объем памяти, необходимый для представления графа, и время на его построение. Протестируйте программу с помощью класса разреженного графа (программа 17.9) и генератора случайных графов (программа 17.12), чтобы иметь возможность выполнять обоснованные эмпирические исследования графов, построенных на базе этой модели.

17.66. Напишите программу, которая генерирует насыщенные случайные графы для специально подобранных наборов значений V и E и выводит объем памяти, необходимый для представления графа, и время на его построение. Протестируйте программу с помощью класса насыщенного графа (программа 17.7) и генератора случайных графов (программа 17.13), чтобы иметь возможность выполнять обоснованные эмпирические исследования графов, построенных на базе этой модели.

17.67. Приведите среднеквадратичное отклонение количества ребер, генерируемых программой 17.13.

17.68. Напишите программу, которая строит каждый возможный граф с точно такой же вероятностью, что и программа 17.13, но затрачивает время и объем памяти, пропорциональные V+E, а не V². Протестируйте программу, как описано в упражнении 17.65.

17.69. Напишите программу, которая строит каждый возможный граф с точно такой же вероятностью, что и программа 17.12, но затрачивает время и объем памяти, пропорциональные E, даже для насыщенности, близкой к 1. Протестируйте программу, как описано в упражнении 17.66.

17.70. Напишите программу, которая генерирует с равной вероятностью каждый возможный граф с Vвершинами и E ребрами (см. упражнение 17.9). Протестируйте программу, как описано в упражнении 17.65 (для ненасыщенных графов) и в упражнении 17.66 (для насыщенных).

17.71. Напишите программу, которая генерирует случайные графы, соединяя вершины, которые упорядочены на сетке размером 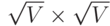, с соседними вершинами (см. рис. 1.2), при этом каждая вершина соединяется к дополнительными ребрами со случайно концевой вершиной (выбор любой концевой вершины равновероятен). Определите, каким должно быть к, чтобы ожидаемое количество ребер было равно E. Протестируйте программу, как описано в упражнении 17.65.

17.72. Напишите программу, которая генерирует случайные орграфы, соединяя вершины, которые упорядочены на сетке размером 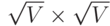, с соседними вершинами, при этом каждое возможное ребро появляется с вероятностью p (см. рис. 1.2). Определите, каким должно быть p, чтобы ожидаемое количество ребер было равно E. Протестируйте программу, как описано в упражнении 17.65.

17.73. Внесите в программу из упражнения 17.72 возможность добавления R дополнительных случайных ребер, вычисленных как в программе 17.12. Для больших R сожмите решетку настолько, чтобы общее количество ребер оставалось примерно равным V.

17.74. Напишите программу, которая генерирует V случайных точек на плоскости, а потом строит граф из ребер, соединяющих все пары точек, удаленных друг от друга на расстояние, не превышающее d (см. рис. 17.13 рис. 17.13 и программу 3.20). Определите, какое значение d следует выбрать, чтобы ожидаемое количество ребер было равно E. Протестируйте программу, как описано в упражнении 17.65 (для ненасыщенных графов) и в упражнении 17.66 (для насыщенных).

17.75. Напишите программу, которая генерирует в единичном интервале V случайные интервалы длиной d, а затем строит соответствующий интервальный граф. Определите, какое значение d следует выбрать, чтобы ожидаемое количество ребер было равно E. Протестируйте программу, как описано в упражнении 17.65 (для ненасыщенных графов) и в упражнении 17.66 (для насыщенных). Указание. Воспользуйтесь BST-деревом.

17.76. Напишите программу, которая случайным образом выбирает V вершин и E ребер из реального графа, найденного в упражнении 17.64. Протестируйте программу, как описано в упражнении 17.65 (для ненасыщенных графов) и в упражнении 17.66 (для насыщенных).

17.77. Один из способов определения транспортной системы -с помощью множества последовательностей вершин, причем каждая такая последовательность определяет путь, соединяющий вершины. Например, последовательность 0-9-3-2 определяет ребра 0-9, 9-3 и 3-2. Напишите программу, которая строит граф по данным из входного файла, содержащего в каждой строке одну последовательность символьных имен. Подготовьте входные данные, которые позволят использовать эту программу для построения графа, соответствующего схеме московского метро.

17.78. Добавьте в решение упражнения 17.77 возможность ввода координат вершин в стиле упражнении 17.60, чтобы можно было работать с графическими представлениями графов.

17.79. Примените преобразования, описанные в упражнениях 17.34—17.37, к различным графам (см. упражнения 17.63—17.76) и сведите в таблицу количество вершин и ребер, удаленных при каждом таком преобразовании.

17.80. Реализуйте конструктор для программы 17.1, который позволит клиентам строить граф разделения без необходимости вызова функции для каждого неявного ребра. То есть количество вызовов функции, необходимых клиенту для построения графа, должно быть пропорционально сумме размеров групп. Разработайте эффективную реализацию этого измененного АТД (на основе структур данных с использованием групп, но без неявных ребер).

17.81. Приведите строгую верхнюю границу количества ребер любого графа разделения для N различных групп с к человек в каждой группе.

17.82. Начертите графы в стиле рис. 17.16, которые содержат V вершин, пронумерованных от 0 до V—1, и ребра, соединяющие вершину i с вершиной , для V= 8, 16 и 32.

17.83. Измените интерфейс АТД из программы 17.1, чтобы позволить клиентам использовать символьные имена вершин и ребра в виде пар экземпляров обобщенного типа Vertex. Полностью скройте от клиентских программ представление, использующее индексацию именами вершин и АТД таблицы символов.

17.84. Добавьте в интерфейс АТД из упражнения 17.83 функцию, которая поддерживает операцию объединить (графы), и напишите реализации для представлений матрицей смежности и списками смежности. Примечание: В результирующем графе должны присутствовать все вершины и ребра каждого исходного графа, но вершины, имеющиеся в обоих графах, должны присутствовать только один раз. Кроме того, нужно удалять параллельные ребра.