Как набирать формулы
Одно над другим
В этом разделе речь пойдет о тех случаях, когда в формуле необходимо поместить один символ над другим. В разд."Операции с пределами и без" уже шла речь о частном случае этой проблемы: постановке " пределов" у знака суммы, интеграла или чего-нибудь еще в этом роде. Сейчас мы рассмотрим общий случай.
Простейшие случаи
Для начала рассмотрим такие возможности расположения одной части формулы над другой:
- Верхняя часть формулы расположена немного выше строки, нижняя — немного ниже (как в дроби, создаваемой командой \frac, но, возможно, без дробной черты).
- Нижняя часть формулы расположена вровень с остальным текстом, верхняя — над ним.
- Над или под фрагментом формулы проведена горизонтальная фигурная скобка, а над или под этой скобкой расположен другой фрагмент формулы.
Разберем эти варианты последовательно.
Начнем с одного дополнения по поводу описанной в первой лекции команды \frac, задающей дроби. Если дробь, заданная с помощью команды \frac, встречается во внутритекстовой формуле, то ее числитель и знаменатель печатаются довольно мелким шрифтом, что не всегда приемлемо. Чтобы этого избежать, можно, подключив пакет amsmath, воспользоваться командой \dfrac: тогда шрифт будет более крупным. Если дробь во внутритекстовой формуле входит в показатель степени или индекс, то иногда имеет смысл задавать ее с помощью команды \tfrac (опять-таки чтобы шрифт был не слишком мелким; эта команда также доступна при подключении amsmath ). Вот примеры:
Теперь о том, как расположить части формулы "так же, как в дроби ", но без дробной черты. Для этого есть два (к сожалению, взаимоисключающих) способа: с подключением пакета amsmath и без этого пакета.
Если у вас подключен пакет amsmath, можно добиться требуемого эффекта с помощью ограничителей и окружения smallmatrix:
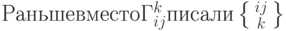 |
Раньше вместо $\Gamma^k_{ij}$
писали $\left\{
\begin{smallmatrix}ij\\k
\end{smallmatrix}\right\}$. |
Конечно, если таких формул у вас в тексте много, пользоваться столь длинными обозначениями немыслимо: нужно на базе smallmatrix разработать сокращенное обозначение (прочтите в "Создание новых команд" , как определять " макросы с параметрами").
Для наиболее часто встречающегося случая "биномиальных коэффициентов", когда ограничителями являются обычные круглые скобки, в пакете amsmath предусмотрена специальная команда \binom, работающая аналогично \frac:
У команды \binom есть также аналоги \dbinom и \tbinom, относящиеся к ней так же, как \dfrac и \tfrac относятся к \frac.
В пакете amsmath предусмотрена также конструкция " обобщенной дроби", предназначенная для создания команд, аналогичных \frac и \binom. По определению, обобщенная дробь — это фрагмент формулы, устроенный так: левый ограничитель, затем дробь (толщина дробной черты может быть произвольной, в том числе нулевой), затем правый ограничитель. Напомним, что ограничители — это скобки и им подобные символы, способные автоматически менять размер; в обобщенной дроби ограничители могут и отсутствовать (так что обычная дробь — действительно частный случай обобщенной). Для набора обобщенной дроби предусмотрена команда \genfrac с шестью аргументами. Чтобы понять, как она работает, посмотрим на пример:
Первый и второй аргументы команды \genfrac — это левый и правый ограничители соответственно; третий аргумент — толщина дробной черты (если толщина нулевая, то дробная черта не печатается); четвертый аргумент содержит указания по поводу размера шрифта для числителя и знаменателя: если оставить его пустым, написав просто "{}" вместо "{0}", то TeX выберет размер самостоятельно; цифра 0 означает, что размер символов будет таким же, как при пользовании командой \dfrac, цифра 1 — размер, как при пользовании командой \tfrac (он же textstyle), цифры 2 и 3 задают еще более мелкие размеры; наконец, пятый и шестой аргументы — это собственно числитель и знаменатель.
Если оставить третий аргумент пустым, написав просто "{}" вместо фигурных скобок, в которых записана толщина, то будет выбрана толщина дробной черты по умолчанию (она равна 0.4 пункта). Если оставить первый и второй аргумент пустыми, то ограничителей не будет (если, однако, левый ограничитель указан, то должен быть указан и правый). Например, "\dfrac{x}{y}" - это то же самое, что
\genfrac{}{}{}{0}{x}{y}В частности, наш пример с символом Кристоффеля можно записать как 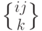
Конечно, команда \genfrac хороша не сама по себе, а как сырье для определения макросов, приспособленных к вашим конкретным нуждам.
Теперь о том, как быть, если вы не подключаете пакет amsmath. В этом случае удобно воспользоваться TeX'овской командой \atop:
В данном случае мы воспользовались еще командами \left и \right для постановки фигурных скобок необходимого размера.
Для биномиальных коэффициентов есть TeX'овская команда \choose \,
Обратите внимание на фигурные скобки, в которые мы заключили
выражение "n\choose k": команда \choose помещает сверху
часть формулы от открывающей фигурной скобки
до \choose,а снизу — часть формулы
от \choose до закрывающей фигурной скобки. Если бы этих фигурных
скобок не было, вниз пошла бы и вся дробь 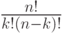 вместе
со знаком равенства.
вместе
со знаком равенства.
Команда \atop определяет, что пойдет вверх, а что — вниз, по тем же правилам, что и \choose. В примере выше с \atop мы обошлись без фигурных скобок, поскольку в математической формуле их функцию исполняют также команды \left и \right.
При подключенном пакете amsmath командами \atop и \choose пользоваться нельзя.
Интересный случай использования дробей — так называемые " цепные дроби"
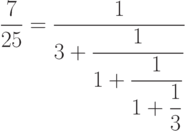
Наивная попытка набрать эту формулу выглядит так:
Результат смотрится не лучшим образом. В разд."Тонкая настройка" объясняется, почему все получилось так плохо и как исправить это положение "вручную", но на практике лучше всего подключить пакет amsmath и сделать так:
Если вы хотите, чтоб какой-то из числителей в цепной дроби был не центрирован, а выключен влево или вправо, надо вместо \cfrac сказать \cfrac[l] или \cfrac[r] соответственно.
Еще один случай, когда надо напечатать две формулы одинакового размера одну под другой, встречается, когда выражение для индексов суммирования занимает несколько строчек. В этом случае надо, подключив пакет amsmath, воспользоваться командой \substack:
В единственном аргументе команды \substack записываются формулы, которые должны быть под знаком суммы (или произведения, или любой другой "операции с пределами"); строчки разделяются знаком |\\| (как и в окружениях, предназначенных для набора матриц).
Рассмотрим случай, когда нижняя часть формулы должна остаться на уровне строки. Чтобы добиться этого эффекта, используется LaTeX'овская команда \stackrel. У этой команды два аргумента: первый — то, что будет над строкой, второй — то, что останется в строке:
Если текст, который надо написать над стрелкой, длинный, прием со \stackrel даст неудовлетворительные результаты. В этом случае надо, подключив пакет amsmath, воспользоваться командами \xleftarrow и \xrightarrow, специально предназначенными для нанесения надписей над и под стрелками. В обязательном аргументе этих команд ставится надпись над стрелкой, в необязательном — под стрелкой (необязательный аргумент, если он есть, ставится перед обязательным). Если надпись длинная, размер стрелки автоматически увеличивается:
Наконец, чтобы нарисовать горизонтальную фигурную скобку под выражением (а под этой скобкой еще, возможно, и сделать подпись), надо воспользоваться командой \underbrace. Аргумент этой команды — тот фрагмент формулы, под которым надо провести скобку; подпись под скобкой, если она нужна, оформляется как нижний индекс. Например, такая формула

получается следующим образом:
$$
\underbrace{1+3+5+7+
\ldots+(2n-1)}_{\mbox{$n$ слагаемых}}=n^2
$$Если у вас подключен пакет amsmath, разумно воспользоваться командой \text вместо \mbox.
Горизонтальная фигурная скобка над фрагментом формулы генерируется командой \overbrace, надпись над ней оформляется как верхний индекс. В одной формуле могут присутствовать горизонтальные фигурные скобки как над, так и под фрагментом формулы:
} В нашем примере нижняя горизонтальная скобка была расположена целиком внутри верхней горизонтальной скобки. Можно сделать и так, чтобы верхняя и нижняя горизонтальные скобки не содержали одна другую, а перекрывались, но для этого нужны дополнительные хитрости

 и
и 
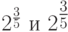

![Формула
$\genfrac{(}{]}{1pt}{0}
{x}{y-z}$
лишена всякого смысла](/sites/default/files/tex_cache/06f432fe79118050f736393716a837b2.png)


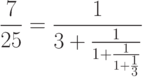
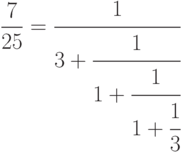
![$$
\sum_{\substack{i\in[0;n]\\
j\in[0;m]}} a_{ij}
$$](/sites/default/files/tex_cache/d521bc664ddf8ee478f83600d723ccda.png)
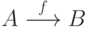
![$$
A\xleftarrow[z]{f}B
\xrightarrow{f+g-h}C
$$](/sites/default/files/tex_cache/7ea9abed2c7bbe9150c4956c9c9ca085.png)