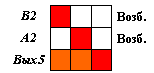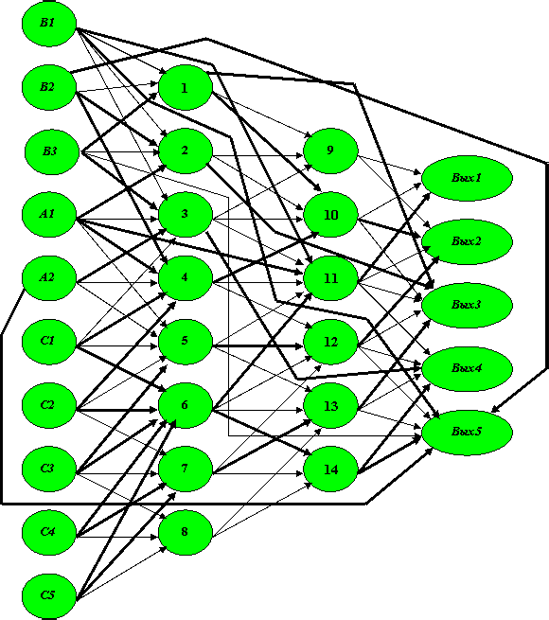
Трассировка нейронной сети

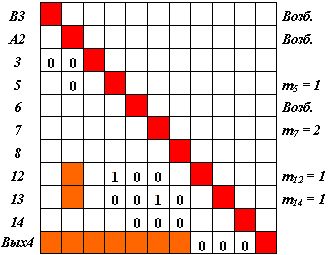
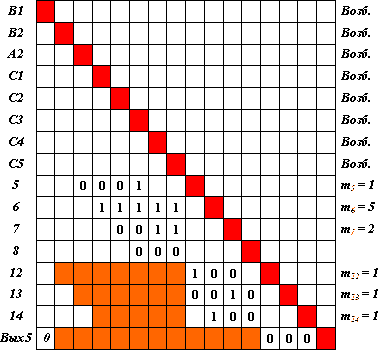
Присваиваем всем нейронам-входам значение "возбужден". Выделяем столбцы, соответствующие входам - первым строкам "возбужденных" нейронов. Это первые семь столбцов. Среди строк этой совокупности столбцов находим строку с максимальным числом единиц в этих столбцах, при отсутствии единиц в других столбцах. Это строка, соответствующая нейрону 6. Теперь нейрон 6 будет представлять нейроны С1, С2, С3, С4, С5, "передавшие" ему свое возбуждение. Присваиваем ему признак "возбужден", исключаем из рассмотрения перечисленные нейроны, матрица S₄ принимает вид как на рис. 4.18.

Рис. 4.18. Шаг преобразования матрицы следования

Для "не возбужденных" нейронов исключаем из матрицы S₄ строки (и столбцы), число единиц в которых стало меньше соответствующего значения m. Они соответствуют нейронам 5 и 7. Повторяем этот шаг до полного исключения таких нейронов, - исключаются нейроны 12 и 13. Матрица имеет вид как на рис. 4.19.

Рис. 4.19. Шаг преобразования матрицы следования

Исключаем из рассмотрения множество "невозбужденных" входов. К таким относится нейрон 8. Выделяем множество столбцов, соответствующих входам матрицы. В их совокупности находим первую строку, обладающую максимальным числом нулей (единиц нет во всей матрице!). Такая строка соответствует нейрону 3. Нули в ней соответствуют нейронам В3 и А2. Исключаем эти нейроны из рассмотрения, полагаем m₃ = 2, присваиваем нейрону 3 признак "возбужден".

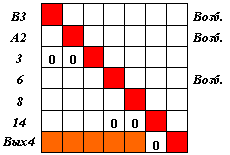
Вновь выделяем множество столбцов, соответствующих входам матрицы, и так как в их совокупности нет строк, содержащих единицы, находим строку с максимальным количеством нулей. Эта строка соответствует нейрону 14. Заменяем в ней нуль на единицу, полагаем m₁₄ = 1, присваиваем нейрону 14 признак "возбужден". Исключаем нейрон 6 из матрицы. Матрица принимает вид как на рис. 4.20.

Рис. 4.20. Шаг преобразования матрицы следования

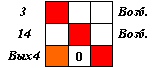
Выделяем множество столбцов, соответствующих входам матрицы, и так как в их совокупности нет строк, содержащих единицы, находим строку с максимальным количеством нулей. Эта строка соответствует нейрону выходного слоя Вых4. Меняем в ней нуль на единицу. Так как это - нейрон выходного слоя, не присваиваем ему признак "возбужден" и значение m. Исключаем нейрон 14 из рассмотрения. Матрица имеет вид как на рис. 4.21.

Рис. 4.21. Шаг преобразования матрицы следования

В этой матрице множество "возбужденных" входов составляет единственный нейрон 3. Однако в его столбце нет ни единичных, ни нулевых элементов. Тогда, как и прежде, вводим в сеть дополнительную связь, найдя в столбце, соответствующем нейрону 3, первую сверху транзитивную связь и положив ее вес равным единице. Эта связь порождает динамический путь возбуждения 3 -> Вых4. Все изменения отражаем в матрице S.

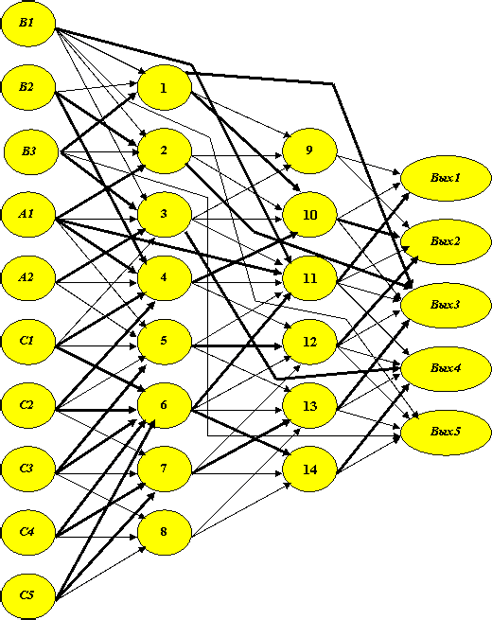
Построение трассы решения R4 закончено. Не приводя промежуточного вида матрицы S, дадим на рис. 4.22 вид сети, полученной после данного этапа трассировки.

И, наконец, приступим к трассировке последнего пути возбуждения. Он осуществляется по обобщенному эталону, требующему решения R5, A2&B1&B2&C1&C2&C3&C4&C5 -> R5. За решением R5 закреплен нейрон выходного слоя Вых5.

На основе текущего вида матрицы S построим матрицу S₅[B1, B2, A2, C1, C2, C3, C4, C5 -> Вых5], исключая из S "ненужные" строки и столбцы и сохраняя транзитивные связи. Затем нам придется исключить из рассмотрения нейрон 4, для которого количество единиц в строке меньше значения m₄ = 4. Получившаяся матрица S₅ представлена на рис. 4.23.

Рис. 4.22. Нейросеть после обучения четырем эталонам

Рис. 4.23. Матрица следования для обучения пятому эталону

Присваиваем всем входам признак "возбужден". Выделяем столбцы, соответствующие "возбужденным" входам. В совокупности этих столбцов находим строку, содержащую максимальное число единиц в этих и только этих столбцах, если таковые имеются. В данном случае это строка, соответствующая нейрону 6. Присваиваем нейрону 6 признак "возбужден" и исключаем из рассмотрения нейроны С1, ..., С5.

Исключаем из рассмотрения нейроны 5 и 7, так как в соответствующих им строках отсутствуют единицы при отличных от нуля значениях m. Однако видно, что после их исключения придется исключить по той же причине нейроны 12 и 13. Получившаяся матрица представлена на рис. 4.24.

Рис. 4.24. Шаг преобразования матрицы следования

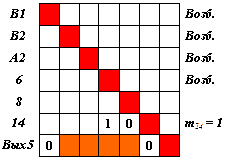
Исключаем из рассмотрения "невозбужденный" вход, соответствующий нейрону 8. Выделяем столбцы, соответствующие "возбужденным" входам, и в их совокупности находим строку, содержащую наибольшее число единиц при отсутствии единиц в других столбцах. Такая строка соответствует нейрону 14. Исключаем из рассмотрения нейрон 6 как передавший свое возбуждение нейрону 14, присваиваем нейрону 14 признак "возбужден". Матрица S₅ принимает вид как на рис. 4.25.

Рис. 4.25. Шаг преобразования матрицы следования

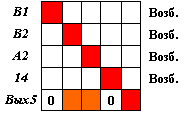
Выделяем столбцы входов, соответствующие "возбужденным" нейронам, и в их совокупности находим строку, содержащую максимальное число нулей (строк с единицами больше нет). Такая строка соответствует нейрону выходного слоя Вых5. Меняем нули на единицы. Исключаем нейроны В1 и 14 из рассмотрения. Отражаем введенные изменения в матрице S. Новый вид матрицы S₅ приведен на рис. 4.26.

Рис. 4.26. Шаг преобразования матрицы следования

Выделяем множество столбцов, соответствующих входам матрицы. В этих столбцах не находим ни строк, содержащих единицы, ни строк, содержащих нули. Тогда в каждом столбце заносим единицы на места транзитивных связей, то есть вводим связи В2 -> Вых5 и А2 -> Вых5, а веса этих связей полагаем равными единице.

Трассировка (обучение сети по обобщенным эталонам ) закончена. Окончательный ее вид представлен на рис. 4.27, где, напоминаем, веса, принявшие значение 1, соответствуют жирным стрелкам.

Рис. 4.27. Обученная нейросеть