Трассировка логической структуры нейросети

"Чтоб бешеной пляской землю овить,

скучную, как банка консервов,

давайте весенних бабочек ловить

сетью ненужных нервов!"

В.В. Маяковский. "Гимн здоровью"

11.1. Задачи обучения нейросети методом трассировки

Под обучением нейросети будем понимать наложение требуемой структуры (обученной) нейросети на заданную графическую структуру.

По логическому описанию СПР мы составляем логическую схему и "объявляем" ее нейросетью, назвав такой подход "схемотехническим". Однако он касался обучения обобщенным эталонам, т.е. воспроизведению потенциально однослойных нейросетей. Там требовалось обеспечить лишь прохождение импульса возбуждения от рецептора к нейрону выходного слоя.

Обобщим метод трассировки, ориентировав его на произвольно структурированное (использующее скобки) логическое описание СПР, в частности, – на его дистрибутивную форму.

Начнем с рассмотрения аналогий.

Задачу трассировки соединений в логической матрице для построения электронной схемы можно представить в двух вариантах.

1. На плате размещены логические элементы. Среди них заданы входные и выходные. Необходимо соединить элементы так, чтобы получить требуемое функциональное устройство. (При ориентации на технологии изготовления электронных плат, например печатных, учитывают дополнительные требования минимизации числа пересечений связей.)
2. На плате размещены логические элементы и в некоторой конфигурации введены связи между ними. Топология связей, при выделении входов и выходов, может быть как случайной, так и регулярной. Необходимо подтвердить существование некоторых связей и ликвидировать другие так, чтобы сформировать требуемое функциональное устройство. При этом может допускаться введение минимального количества недостающих связей.

Как правило, при таких постановках задачи трассировки не рассматриваются обратные связи.

Исходя из аналогий, обусловленных общей логической базой, сформулируем и решим две задачи построения обученной (обучения) нейронной сети в соответствии с ее специализацией в составе СПР.

Используя предложенную нам для обучения нейросеть, позволим ее модификацию – введение недостающих связей (отвергнуть негодную сеть – значит, рассчитывать на случай), если очевидно, что без таких связей правильного функционирования добиться невозможно.

11.2. Формирование обученной нейросети на основе заданного множества нейроподобных элементов

Под нейроподобным элементом, который мы условились называть нейроном, подразумевается не столько овеществленный образ – электронный аналог, программный модуль и др., сколько реализуемая им передаточная функция.

Пусть задано множество нейронов X = {x₁, ..., x_m} и логическое описание СПР в дистрибутивной форме ^{1Напоминаем, что здесь не рассматриваются обратные связи} По "логической" технологии, обоснованной ранее, необходимо сформировать связи между нейронами так, чтобы при единичных значениях достоверности, совпадающих с единичными булевыми значениями переменных, максимального возбуждения на выходном слое при данной передаточной функции достигал тот нейрон, который закреплен за решением, обусловленным единичным значением соответствующей ему логической функции.

Скобочная запись задает последовательность формирования обученной нейросети. Процесс такого формирования (обучения) заключается в рекурсивной коммутации подструктур – термов на основе содержимого скобок в соответствии с их вложенностью.

Продолжим рассмотрение примера на основе логического описания (10.1). Перепишем его, используя символ обобщенной операции, реализуемой передаточной функцией, но сохранив скобки:

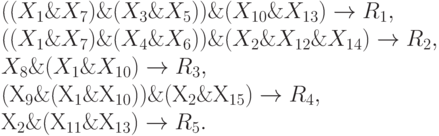( 11.1)

Прежде всего из множества Х необходимо выделить нейроны входного – рецепторного – и выходного слоев. Исходя из этого, а также, задав количество необходимых и предполагаемых нейронов разного функционального назначения, закрепим и переобозначим нейроны: Х = {X₁, ..., X₁₅, 1, ..., 11, R₁, ..., R₅}. Нейроны 1, ..., 11 в будущих построениях исполнят роль нейронов скрытых слоев – скрытых нейронов.

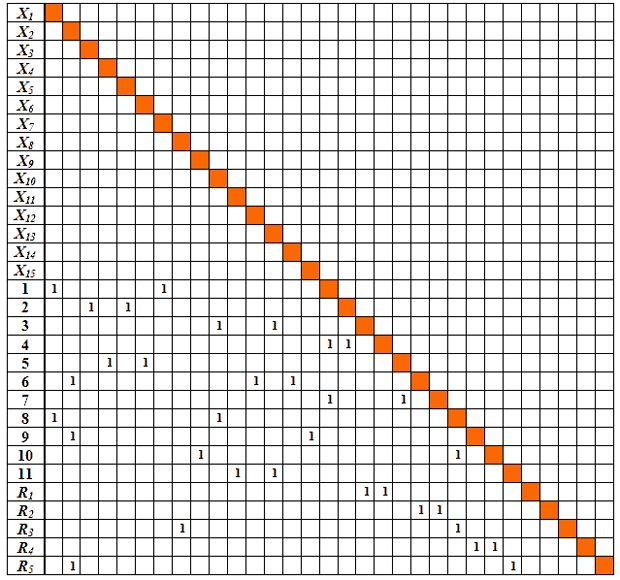
Составим матрицу следования, первоначально содержащую "пустые" элементы. На рис. 11.1 представлена такая матрица S, соответствующая уже полученному решению. Однако пока не следует учитывать единичные элементы: их необходимо сформировать в процессе решения задачи.

Для удобства пользования и учитывая, что данная матрица при отсутствии обратных связей – треугольная, она выполнена в виде "шахматки", где диагональные элементы отмечены.

Итак, чтобы сигналы возбуждения направленно проходили от входных нейронов к выходным, необходимо сформировать связи с единичными весами, используя скрытые нейроны. Пусть скрытые нейроны образуют ресурс – множество М свободных нейронов, первоначально M = {1, ..., 11}.

Рис. 11.1. Матрица следования после обучения нейросети

Организуем последовательный анализ выражений (11.1).

При просмотре первого выражения, анализируя открывающие и закрывающие скобки, найдем первую скобку самого высокого уровня вложенности. Она соответствует выражению (Х₁ & Х₇). Закрепим за ним первый свободный нейрон 1 из М, предположив тем самым, что он выполняет аналог операции, указанной в скобках. Сформируем уточненную строку матрицы следования S, соответствующую нейрону 1, записав веса связей, равные единице, в столбцы, соответствующие нейронам Х₁ и Х₇.

Обозначим исследованную "скобку" именем нейрона 1 и перепишем логическое выражение:

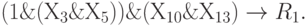
Продолжим поиск "скобок" самого высокого уровня вложенности.

Находим "скобку" (Х₃ & Х₅). В общем случае такая "скобка" могла встретиться ранее, и за ней мог быть закреплен скрытый нейрон. В целях экономии нейронов сформируем уточненную строку матрицы следования, записав единицы в столбцах, соответствующих нейронам Х₃ и Х₅. Однако, прежде чем поместить строку на ее место, проверим, нет ли в S идентичной строки? В данном случае такой строки нет. Тогда соотнесем полученную строку с очередным свободным нейроном 2 и поместим ее в S.

Перепишем логическое выражение, заменив обработанную "скобку":

(1&2)&(Х₁₀&Х₁₃)->R₁ .

Продолжая так же, закрепим нейрон 3 за "скобкой" (Х₁₀&Х₁₃) и сформируем соответствующую этому нейрону строку матрицы S. Запись логического выражения примет вид

(1&2)&3 -> R₁ .

Следующий обзор этой записи приводит к замене "скобки" 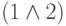именем нейрона 4 и к формированию строки матрицы следования, соответствующей этому нейрону. Эта строка содержит единицы в строках, соответствующих нейронам 1 и 2. Запись логического выражения примет вид

4 & 3 -> R₁.

Отсутствие скобок говорит о необходимости введения связей 4 -> R₁ и 3 -> R₁. Таким образом, строка, соответствующая нейрону R₁ выходного слоя, содержит единицы в столбцах, соответствующих нейронам 3 и 4.

Трассировка решения R₁ закончена.

Анализируем логическое выражение

((X₁ & X₇ )& (X₄ & X₆ )) &(X₂ & X₁₂ & X₁₄ ) -> R₂ .

Строка матрицы S, сформированная по "скобке" (Х₁&Х₇), совпадает со строкой, соответствующей нейрону 1. Значит, можно "сэкономить", повторно использовав этот нейрон. Преобразуем запись:

(1& (X₄ & X₆ )) &(X₂ & X₁₂ & X₁₄ ) -> R₂ .

За следующей "скобкой" (Х₄ &Х₆) закрепим нейрон 5, сформировав для него строку матрицы S, и запись примет вид

(1& 5) &(X₂& X₁₂ & X₁₄ ) -> R₂ .

Продолжив ее обзор, получим новый вид записи (1 & 5) & 6 -> R₂ , а затем 7 & 6 -> R₂ . Сформированные при этом строки матрицы S показаны на рисунке. Аналогично анализируются другие логические выражения (11.1), что не вносит новых особенностей в неформально изложенный алгоритм.

Нейросеть, представленная матрицей следования S, близка к нейросети, показанной на рис. 10.2.