Трассировка логической структуры нейросети

11.4. Обучение-трассировка нейросети заданной структуры

Как видно из примера, рассмотренного в "Корректировка параметров, дистрибутивные преобразования, однослойные и совершенные логические нейронные сети" , если нейросеть не может быть сведена к однослойной на заданной графической структуре, то при трассировке необходимо следовать структуре логического выражения. Это требует такой структуризации обучаемой нейросети, при которой "скобки" в порядке их вложенности соответствуют выделенным подструктурам сети. Тогда подструктуры нейросети образуют расширяемый ресурс, предоставляемый для реализации "скобок", – от максимального уровня вложенности до нулевого.

В рассматриваемой сети (рис. 11.2) максимальная длина статического пути возбуждения равна трем. Более того, данная нейросеть является трехслойной в "традиционном" смысле [13, 15, 19, 20], т.е. в ней нет связей "через слой".

Запишем первое логическое выражение из описания (11.1):

((X₁& X₇)& (X₃& X₅)) &(X₁₀& X₁₃) -> R₁.

Ему соответствует максимальная длина логических цепочек, равная трем, что следует из порядка вложенности скобок. Тогда справедливо предположение о том, что "скобки" (X₁&X₇) и (X₃&X₅) могут быть реализованы не далее чем на первом слое (3 - 2 = 1), чтобы не воспрепятствовать формированию подструктур, в которые они входят. Охватывающая их "скобка" ((X₁&X₇)&(X₃&X₅)) должна быть реализована на втором слое. Не далее чем на этом же, т.е. на невыходном, слое может быть реализована и скобка (X₁₀& X₁₃).

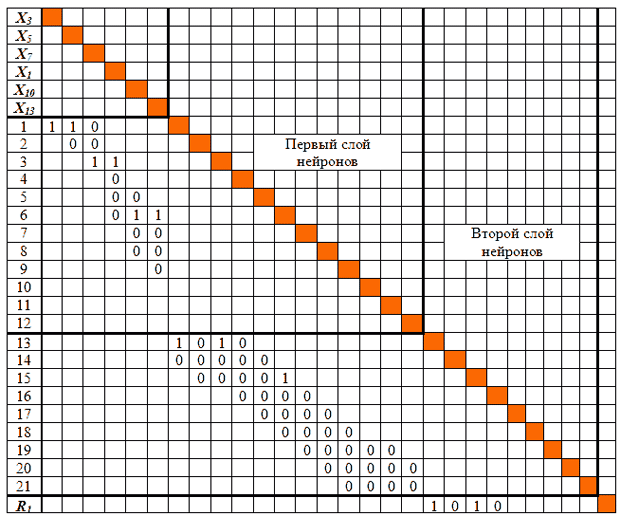
Предположим, что сквозная нумерация позволяет выделить подмножества нейронов, принадлежащих одному слою или, в общем случае, имеющих одинаковую максимальную длину статической цепочки, как показано на рис. 11.2. Действительно, нейроны 1-12 образуют первый слой нейросети, нейроны 13-21 – второй слой, третий слой – выходной. Тогда и в описывающей нейросеть матрице следования S, наличие которой лишь подразумевается ввиду ее громоздкости, можно отчеркнуть строки и столбцы нейронов, принадлежащих, в данном случае, одному слою. (Напомним, что в матрице S связи обозначаются значениями весов, первоначально равными нулю.)

Построим матрицу S₁ (рис. 11.3) на основании выражения, определяющего решение R₁.

Для ее построения необходимо из матрицы S исключить строки (и столбцы), которые соответствуют переменным, не участвующим в построении решения R₁, а также – представительство других решений на выходном слое.

Приступим к реализации первой "скобки" третьего уровня вложенности.

В столбцах, соответствующих событиям Х₇ и Х₁, ведя поиск в пределах нейронов первого слоя, найдем первую строку, которая содержит максимальное число нулей, указывающих наличие связей. Такая строка, где нули находятся во всех выделенных столбцах, соответствует нейрону 3. В матрицах S и S₁ меняем эти нули на единицы – формируем единичные веса связей. В матрице S при строке, соответствующей нейрону 3, указываем число введенных единиц, m₃ = 2. В записи выражения меняем "скобку" на имя нейрона, реализующего ее. Запись принимает вид

(3& (X₃& X₅)) &(X₁₀& X₁₃) -> R₁.

Перейдем к реализации "скобки" (X₃& X₅) того же уровня вложенности.

Рис. 11.3. Матрица S1 после трассировки решения R1

В столбцах, соответствующих нейронам X₃ и X₅, найдем строку, содержащую максимальное число нулей. Такая строка соответствует нейрону 1 первого слоя. Меняем в S и S₁ найденные нули на единицы, в матрице S указываем значение m₁ = 2. Преобразуем запись выражения:

(3& 1) &(X₁₀& X₁₃) -> R₁.

Скобка (X₁₀& X₁₃) может быть реализована как на первом, так и на втором слое. В столбцах, соответствующих нейронам X₁₀ и X₁₃, находим первую строку, содержащую максимальное число нулей. Такая строка соответствует нейрону 6. Меняем выделенные нули на единицы и указываем число таких единиц в S: m₆ = 2. Запись выражения преобразуется:

(3& 1) & 6 -> R₁.

Анализируя столбцы, соответствующие нейронам 1 и 3, находим нейрон 13 второго слоя, реализующий скобку (3& 1), отмечаем значение m₁₃ = 2. Запись выражения преобразуется к виду

13& 6 -> R₁.

Анализируя столбцы, соответствующие нейронам 6 и 13, включив в рассмотрение нейроны выходного слоя, находим первую строку, содержащую максимальное число нулей. Такая строка соответствует нейрону 15. Однако она содержит нуль лишь в столбце нейрона 6. Меняем этот нуль в матрицах S и S₁ на единицу, полагаем m₁₅ = 1. Запись выражения преобразуется к виду

13&15 -> R₁.

Затем реализуем единственную "скобку" нулевого уровня вложенности с помощью нейрона R₁. Трассировка первого решения закончена. В результате ее введены отмеченные на рисунке связи Х₃ -> 1, Х₅ -> 1, Х₇ -> 3, Х₁ -> 3, Х₁₀ -> 6, Х₁₃ -> 6, 1 -> 13, 3 -> 13, 6 -> 15, 13 -> R₁, 15 -> R₁.

Для трассировки решения

((X₁&X₇)&(X₄&X₆))&(X₂&X₁₂& X₁₄) -> R₂

построим матрицу следования S₂ (рис. 11.4). Для этого исключим из матрицы S все нейроны- рецепторы, не участвующие в приведенной выше записи выражения, а также неиспользуемые нейроны выходного слоя. Затем с помощью одного просмотра сверху вниз исключим представительство тех нейронов, где число единиц в строках меньше соответствующего значения m.

При анализе "скобки" (X₁& X₇) обнаруживаем в столбцах, соответствующих нейронам X₁ и X₇, две единицы в строке, соответствующей нейрону 3, при том, что m₃ = 2. Запись выражения преобразуется к виду

(3 & (X₄& X₆)) &(X₂& X₁₂& X₁₄) -> R₂.

В строке, соответствующей Х₄ и Х₆, нет строки, содержащей единицы во всех позициях. Находим первую строку, соответствующую нейрону первого слоя и содержащую максимальное число нулей при нулевом значении m. Такая строка, содержащая нули во всех позициях, соответствует нейрону 2. В матрицах S и S₂ меняем выделенные нули на единицы, фиксируем значение m₂ = 2. Запись выражения преобразуется:

(3 &2) &(X₂& X₁₂& X₁₄) -> R₂.

В соответствии с уровнем вложенности присутствующие в записи "скобки" могут быть реализованы как на первом, так и на втором слое нейросети. В столбцах, соответствующих Х₂, Х₁₂, Х₁₄, нет строки нейрона первого или второго слоя, содержащей единицы во всех столбцах. Находим первую строку, содержащую максимальное число нулей при нулевом значении m. Такая строка соответствует нейрону 7. Меняем выделенные нули на единицы, фиксируем значение m₇ = 2. Запись выражения принимает вид

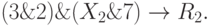( 11.2)