|
Раньше это можно было зделать просто нажав на тест и посмотреть результаты а сейчас никак |
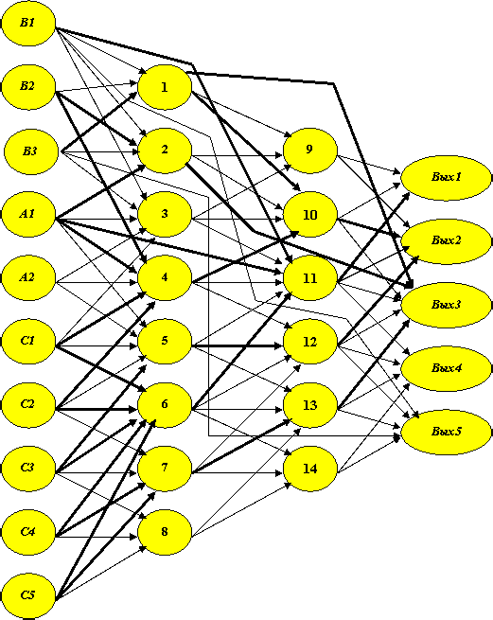
Трассировка нейронной сети
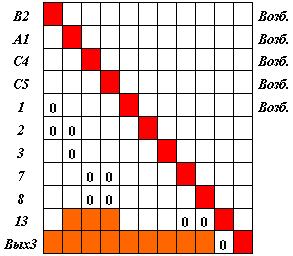
Присваиваем всем нейронам, образующим входы матрицы, признак "возбужден".
Выделяем и объединяем столбцы, соответствующие входам матрицы S3.
Разовьем предшествующие аналогичные действия следующим образом.
В выделенных столбцах находим строку, содержащую хотя бы одну единицу. Она (строка) представляет тот нейрон, который "собрал" (при анализе предыдущих эталонов) возбуждение одного или более нейронов, образующих входы. Эти нейроны, "передавшие" свое возбуждение, могут быть исключены из рассмотрения. Среди таких строк выбираем строку с максимальным числом единиц.
Так, нейрон 1 возбужден единственным нейроном, принадлежащим текущему множеству входов матрицы, - нейроном В3. Впредь он представляет этот нейрон, который может быть исключен из рассмотрения. Матрица S3 принимает вид на рис. 4.13.
Подтверждаем нейрону 1 признак "возбужден" и превращаем его во вход матрицы S3, уничтожив веса в его строке.
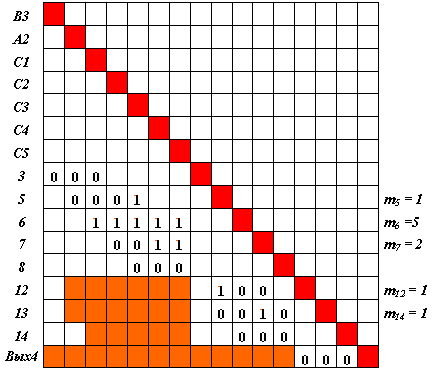
Вновь находим множество входов матрицы и выделяем соответствующие им столбцы. Пытаемся найти строку, содержащую единицы в этих и только этих столбцах, но таких больше нет. Тогда находим строку, содержащую максимальное число нулей. Первая такая строка соответствует нейрону 2. "Объединяем" на нем возбуждение нейронов В2 и А1, заменяя нули единицами. Полагаем m2 = 2, исключаем нейроны В2 и А1 из рассмотрения, присваиваем нейрону 2 признак "возбужден". Отражаем сделанные изменения весов в матрице S.
Исключаем входы, не обладающие признаком "возбужден", - нейроны 3 и 5.
Выделяем столбцы, соответствующие входам. В их совокупности не находим строк, содержащих единицы. Тогда находим строку, содержащую максимальное число нулей. Такая строка соответствует нейрону 7. Меняем нули (в выделенной совокупности столбцов!) на единицы, полагаем m7 = 2, присваиваем нейрону 7 признак "возбужден", отражаем изменение весов в матрице S. Исключаем нейроны С4 и С5 из рассмотрения. Сразу замечаем, что сформируется "невозбужденный" вход, соответствующий нейрону 8. Исключаем из рассмотрения и этот нейрон (рис. 4.14).
Выделяем столбцы, соответствующие "возбужденным" входам, и не находим строк, содержащих единицы. Тогда находим первую строку, содержащую максимальное число нулей. Это строка, соответствующая нейрону 13. Меняем нуль на единицу, нейрону 13 присваиваем признак "возбужден", полагаем m13 = 1. Исключаем нейрон 7 из рассмотрения.
Выделяем столбцы, соответствующие множеству "возбужденных" входов. В них не находим строку с единицами, но единственная строка с максимальным числом нулей соответствует нейрону Вых3. Меняем нуль на единицу. Однако статус этого нейрона особый, и значение m, как и признак "возбужден", ему не присваиваем.
Исключаем нейрон 13 из рассмотрения.
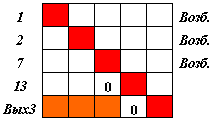
Выделяем множество столбцов, соответствующих "возбужденным" входам. Это столбцы, соответствующие нейронам 1 и 2. Пытаемся в этих столбцах найти строку с единицами, затем с максимальным числом нулей, - но таковых нет! Значит, необходимо введение дополнительных связей. Тогда в каждом столбце при просмотре сверху вниз находим первую транзитивную связь и меняем ее на единицу. Это означает, что данная сеть дополняется динамическими цепочками возбуждения 1 -> Вых3 и 2 -> Вых3.
Построение трассы решения R3 закончено. После этого этапа обучения сеть имеет вид как на рис. 4.15.
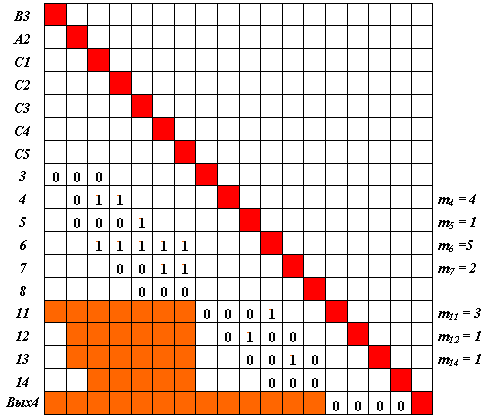
Приступим к обучению следующему обобщенному эталону - решению A2&B3&C1&C2&C3&C4&C5 -> R4. Матрица следования S4[B3, A2, C1, C2, C3, C4, C5 -> Вых4] представлена на рис. 4.16.
Исключим из рассмотрения те нейроны, для которых количество единиц в строках меньше значения m. Такими нейронами являются 4 и 11. Матрица S4 имеет вид как на рис. 4.17.