|
В лекции 3 часть номер 2 приведён пример нахождения транзитивного замыкания по матрице смежности. Из примера для обратного транзитивного замыкания видно, что путь для достижения вершины х6 в вершину х3 равен 3, а не 2, как показано в табличном примере. Мне кажется, что в лекции ошибка. |
Лекция 7: Методы разбиения графа на максимальные сильно связные подграфы
Матричный метод разбиения
Метод разбиения графа на максимальные сильно связные подграфы по матрицам достижимости R и контрдостижимости Q состоит в следующем.
- По матрице смежности строится матрица достижимости R. Используя операцию транспонирования, находим матрицу контрдостижимости Q.
- Находится матрица C = { сij }, i,j = 1, 2, 3, ..., n, где n – число вершин исходного графа, а каждый элемент
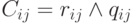 , т. е. матрица C получается поэлементным логическим умножением матриц R и
, т. е. матрица C получается поэлементным логическим умножением матриц R и 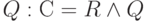 .
. - Элементы, имеющие одинаковые строки и столбцы в матрице С группируем перестановкой строк и столбцов, получаем блочно диагональную матрицу Св , где каждая группа элементов и есть максимальный сильно связный подграф.
Рассмотрим пример разбиения для графа, представленного на рис. 7.1,а. Как следует из определения матрицы R для ее нахождения следует для каждой вершины найти прямое транзитивное замыкание. Если некоторая xj вершина графа входит в транзитивное замыкание T+(хi), то элемент матрицы R rij =1. Полученные таким образом матрицы R и Q показаны на таблица 7.7а и таблица 7.7б. В результате логического умножения получили матрицу С ( таблица 7.7в), в которой находим одинаковые строки. Например, для вершины х1 строка совпадает с седьмой и одиннадцатой. Следовательно, вершины х1, х7, х11 группируем вместе и они составляют первый выделенный подграф. Как видим из блочнодиагональной матрицы ( таблица 7.7г) полученные подграфы совпадают с результатом разбиения по методу Мальгранжа .
