|
В лекции 3 часть номер 2 приведён пример нахождения транзитивного замыкания по матрице смежности. Из примера для обратного транзитивного замыкания видно, что путь для достижения вершины х6 в вершину х3 равен 3, а не 2, как показано в табличном примере. Мне кажется, что в лекции ошибка. |
Вятский государственный университет
Опубликован: 07.04.2008 | Доступ: свободный | Студентов: 3267 / 856 | Оценка: 4.31 / 3.94 | Длительность: 06:04:00
Специальности: Программист, Математик
Теги:
Лекция 7: Методы разбиения графа на максимальные сильно связные подграфы
РАЗБИЕНИЕ – 3
| X3 | X4 | X5 | X6 | X8 | X9 | X10 | T+(x3) | |||
|---|---|---|---|---|---|---|---|---|---|---|
| X3 | 1 | 1 | 1 | 1 | 0 | |||||
| X4 | 1 | 1 | 1 | |||||||
| X5 | 1 | 2 | ||||||||
| A= | X6 | 1 | 1 | |||||||
| X8 | ||||||||||
| X8 | ||||||||||
| X9 | 1 | 1 | ||||||||
| X10 | 1 | 1 | 1 | 1 | ||||||
| T-(x3) | 0 | 1 | 2 |
- Выберем, например, вершину х3 ( таблица 7.3) T+(х3) = { х3, х4, х5, х9, х10}, T-(х3) = { х3, х9, х10 }.
-
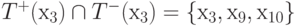 . Следовательно, третий подграф G3
состоит из вершин х3
, х9
, х 10
, матрица смежности которого показана на
таблица
7.3.
. Следовательно, третий подграф G3
состоит из вершин х3
, х9
, х 10
, матрица смежности которого показана на
таблица
7.3. - G ' = G \G3; G ' = (X ', A'); X ' = { х4, х5, х6, х8 }.
-
 следовательно, процесс разбиения продолжаем: G' -> G; X ' -> X.
следовательно, процесс разбиения продолжаем: G' -> G; X ' -> X.
РАЗБИЕНИЕ – 4
- Выберем
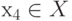 (
таблица
7.5 ) T+(х4) = { х4, х5 }; T-(х4) = { х4, х5 ).
(
таблица
7.5 ) T+(х4) = { х4, х5 }; T-(х4) = { х4, х5 ). -
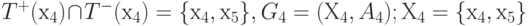 , матрица смежности A4
показана на
таблица
7.6.
, матрица смежности A4
показана на
таблица
7.6. - G ' = G \G4; G ' = (X ', A'); X ' = { х6, х8 }.
-
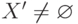 , следовательно, переходим к пятому разбиению.
, следовательно, переходим к пятому разбиению.
РАЗБИЕНИЕ – 5
- Выберем х6 . T+(х6) = { х6, х8 }; T-(х6) = { х6 }.
-
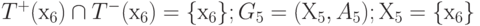 .
. - G ' = G \G5; X ' = { х8 }.
-
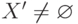 , но состоит из одной вершины, поэтому очевидно, что шестой подграф содержит вершину х8
. На этом процесс разбиения завершается.
, но состоит из одной вершины, поэтому очевидно, что шестой подграф содержит вершину х8
. На этом процесс разбиения завершается.
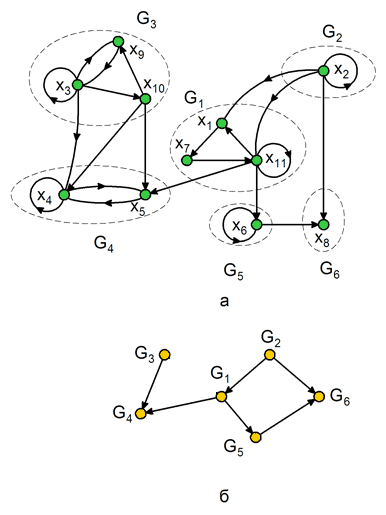
Итак, результат разбиения:
G1 =( Х1, A1 ), Х1 = { х1, х7, х11 },
G2 = ( Х2, A2 ), Х2 = { х2 },
G3 = ( Х3, A3 ), Х3 = { х3, х9, х10 },
G4 = ( Х4, A4 ), Х4 = { х4, х5 },
G5 = ( Х5, A5 ), Х5 = { х6 },
G6 = ( Х6, A6 ), Х6 = { х8 }
показан на рис. 7.2,а, где каждый подграф G1, ... ,G6 представляет собой сильную компоненту графа. Граф G* =(X*, A* ), в котором в качестве элементов выступают сильные компоненты, называется конденсацией ( рис. 7.2,б).