НОУ ИНТУИТ | Менеджмент организации. Лекция 8: Моделирование ситуаций и разработка решений

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 03.08.2017 | Уровень: для всех | Доступ: платный

|

Вам нравится? Нравится 70 студентам

| Поделиться |

Поддержать программу

8.3.4. Характеристика способов принятия решений на основе детерминированного факторного анализа

При принятии решений на основе детерминированного факторного анализа в качестве ключевого вопроса рассматривают определение влияния изменения отдельного фактора 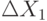$\Delta X_1$ на прирост результативного показателя 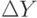$\Delta Y$ при фиксированных значениях остальных воздействий Х₂...Х_n.

Так, например, метод цепных подстановок заключается в определении ряда промежуточных значений результативного показателя y путем последовательной замены базисной величины каждого воздействующего факторного a₀, b₀, c₀, d₀ на отчетную a₁, b₁, c₁, d₁. В результате чего обеспечивается выделение влияния каждого фактора. Например, связь между результативным показателем y и воздействующими факторами a, b, c, d определяется мультипликативной моделью:

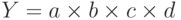$Y = a \times b \times c \times d$ .

Тогда базисное значение Y₀ рассчитывается по формуле:

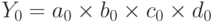$Y_0 = a_0 \times b_0 \times c_0 \times d_0$ .

Отчетное значение результативного показателя Y₁ определяется выражением:

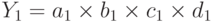$Y_1 = a_1 \times b_1 \times c_1 \times d_1$ .

Условные значения результативного показателя y_а, y_b, y_с, y_d рассчитываются соответственно из выражений:

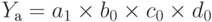$Y_а = a_1 \times b_0 \times c_0 \times d_0$ .

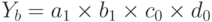$Y_b = a_1 \times b_1 \times c_0 \times d_0$ .

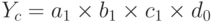$Y_c = a_1 \times b_1 \times c_1 \times d_0$ .

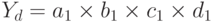$Y_d = a_1 \times b_1 \times c_1 \times d_1$ .

Тогда влияние каждого фактора на результат можно описать в виде:

$\Delta Y_а = Y_а – Y_0$ .

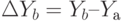$\Delta Y_b = Y_b – Y_а$ .

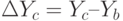$\Delta Y_c = Y_c – Y_b$ .

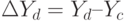$\Delta Y_d = Y_d – Y_c$ .

Индексный способ основан на вычислении относительных показателей динамики, пространственных сравнений, выполнения плана (норматива, прогноза) и т. д.

Основной формой индекса является агрегатный (от лат. agregatus - складываемый, суммируемый), в котором числитель и знаменатель представляют собой набор ("агрегат") непосредственно несоизмеримых и неподдающихся суммированию элементов - сумму произведений двух величин, одна из которых меняется (индексируется), а другая остается неизменной (вес индекса).

Примером общего индекса количественных показателей может служить агрегатный индекс стоимости продукции или товарооборота:

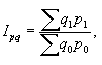
где	$\Sigma q_1 p_1$	-	стоимость продукции отчетного периода;
	$\Sigma q_0 p_0$	-	стоимость продукции базисного периода;
	p₁, p₀	-	цены единицы продукции в отчетном и базисном периоде соответственно (p - от лат. pretium);
	q₁, q₀	-	количество какой-либо продукции в натуральном выражении в отчетном и базисном периоде соответственно (q - от лат. quantitas).

Индекс I_pq показывает, во сколько раз изменилась стоимость продукции отчетного периода по сравнению с базисным.

Агрегатный индекс физического объема продукции I_q отражает изменение только одного фактора - индексируемого показателя объема продукции q, реализуемой по одним и тем же ценам, например базисным p₀:

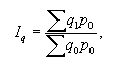
Этот же общий индекс физического объема I_q можно представить в форме среднего арифметического индекса:

где

i_q = q₁ : q₀

-

индивидуальный индекс объема продукции.

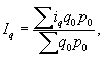
Такой индекс используется, например, когда неизвестны количества произведенных отдельных видов продукции в натуральных измерениях, но известны индивидуальные индексы i_q и общая стоимость продукции базисного периода q₀p₀.

В аналитических целях может быть также использован общий индекс физического объема I_q, представленный в форме среднего гармонического индекса:

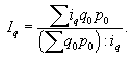
Рассмотренные выше общие индексы рассчитываются для количественных показателей. Наряду с ними широкое распространение получили общие индексы качественных показателей.

Характерными примерами общих индексов качественных показателей являются агрегатные индексы цен.

Агрегатный индекс с весами объема продукции по отчетному периоду, предложенный в 1874 г. немецким экономистом Г. Паше, вычисляют по формуле:

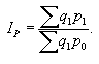
где	$\Sigma q_1 p_1$	-	фактическая стоимость товаров в отчетном периоде;
	$\Sigma q_1 p_0$	-	условная стоимость товаров, реализованных в отчетном периоде по ценам базисного периода.

Агрегатный индекс с весами объема продукции по базисному периоду, предложенный в 1864 г. немецким экономистом Э. Ласпейресом, вычисляют по формуле:

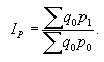
Значения индексов цен Паше и Ласпейреса для одних и тех же данных не совпадают, так как имеют различное экономическое содержание. Индекс цен Паше характеризует изменение цен отчетного периода по сравнению с базисным по товарам, реализованным в отчетном периоде и фактическую экономию (или перерасход) от изменения цен. Индекс цен Ласпереса характеризует изменение цен отчетного периода по сравнению с базисным по товарам, реализованным в базисном периоде и экономию (или перерасход), которую можно было бы получить от изменения цен (т. е. условную экономию).

Дальше >>

Менеджмент организации

Менеджмент организации

Моделирование ситуаций и разработка решений

8.3.4. Характеристика способов принятия решений на основе детерминированного факторного анализа

Вопросы и ответы

Студенты

Авторизоваться

Менеджмент организации

Менеджмент организации

Моделирование ситуаций и разработка решений

8.3.4. Характеристика способов принятия решений на основе детерминированного факторного анализа

Вопросы и ответы

Студенты