|
Здравствуйте! 4 июня я записалась на курс Прикладная статистика. Заплатила за получение сертификата. Изучала лекции, прошла Тест 1. Сегодня вижу, что я вне курса! Почему так произошло? |
Статистика интервальных данных
12.6. Интервальный кластер-анализ
Кластер-анализ, как известно [ [ 12.38 ] ], имеет целью разбиение совокупности объектов на группы сходных между собой. Многие методы кластер-анализа основаны на использовании расстояний между объектами. (Степень близости между объектами может измеряться также с помощью мер близости и показателей различия, для которых неравенство треугольника выполнено не всегда.) Рассмотрим влияние погрешностей измерения на расстояния между объектами и на результаты работы алгоритмов кластер-анализа.
С ростом размерности  евклидова пространства диагональ единичного куба растет как
евклидова пространства диагональ единичного куба растет как  . А какова погрешность определения евклидова расстояния? Пусть двум рассматриваемым векторам соответствуют
. А какова погрешность определения евклидова расстояния? Пусть двум рассматриваемым векторам соответствуют 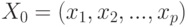 и
и  - векторы размерности
- векторы размерности  . Они известны с погрешностями
. Они известны с погрешностями 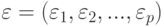 и
и 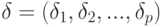 , т.е. статистику доступны лишь векторы
, т.е. статистику доступны лишь векторы 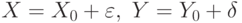 Легко видеть, что
Легко видеть, что
 |
( 73) |
Пусть ограничения на абсолютные погрешности имеют вид

Такая запись ограничений предполагает, что все переменные имеют примерно одинаковый разброс. Трудно ожидать этого, если переменные имеют различные размерности. Однако рассматриваемые ограничения на погрешности естественны, если переменные предварительно стандартизованы, т.е. центрированы и отнормированы (из каждого значения вычтено среднее арифметическое, а разность поделена на выборочное среднее квадратическое отклонение).
Пусть  . Тогда последнее слагаемое в (73) не превосходит
. Тогда последнее слагаемое в (73) не превосходит  поэтому им можно пренебречь. Тогда из (73) следует, что нотна евклидова расстояния имеет вид
поэтому им можно пренебречь. Тогда из (73) следует, что нотна евклидова расстояния имеет вид

 имеют одинаковые математические ожидания и для них справедлив закон больших чисел (эти предположения естественны, если переменные перед применением кластер-анализа стандартизованы), то существует константа
имеют одинаковые математические ожидания и для них справедлив закон больших чисел (эти предположения естественны, если переменные перед применением кластер-анализа стандартизованы), то существует константа 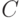 такая, что
такая, что
 и
и  .
.Из рассмотрений настоящего пункта вытекает, что
 |
( 74) |
 таком, что
таком, что  .
.Какое минимальное расстояние является различимым? По аналогии с определением рационального объема выборки при проверке гипотез предлагается уравнять слагаемые в (74), т.е. определять минимально различимое расстояние  из условия
из условия
 |
( 75) |
Естественно принять, что расстояния, меньшие \rho_{min}, не отличаются от 0, т.е. точки, лежащие на расстоянии  , не различаются между собой.
, не различаются между собой.
Каков порядок величины 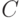 ? Если
? Если 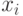 и
и  независимы и имеют стандартное нормальное распределение с математическим ожиданием 0 и дисперсией 1, то, как легко подсчитать,
независимы и имеют стандартное нормальное распределение с математическим ожиданием 0 и дисперсией 1, то, как легко подсчитать, 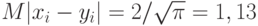 и соответственно
и соответственно  . Следовательно, в этой модели
. Следовательно, в этой модели
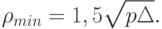
Формула (75) показывает, что хотя с ростом размерности пространства  растет диаметр (длина диагонали) единичного куба - естественной области расположения значений переменных, с той же скоростью растет и естественное квантование расстояния с помощью порога неразличимости , т.е. увеличение размерности (вовлечение новых переменных), вообще говоря, не улучшает возможности кластер-анализа.
растет диаметр (длина диагонали) единичного куба - естественной области расположения значений переменных, с той же скоростью растет и естественное квантование расстояния с помощью порога неразличимости , т.е. увеличение размерности (вовлечение новых переменных), вообще говоря, не улучшает возможности кластер-анализа.
Можно сделать выводы и для конкретных алгоритмов. В дендрограммах (например, результатах работы иерархических агломеративных алгоритмах ближнего соседа, дальнего соседа, средней связи) можно порекомендовать склеивать (т.е. объединять) уровни, отличающиеся менее чем на  . Если все уровни склеятся, то можно сделать вывод, что у данных нет кластерной структуры, они однородны. В алгоритмах типа "Форель" центр тяжести текущего кластера определяется с точностью
. Если все уровни склеятся, то можно сделать вывод, что у данных нет кластерной структуры, они однородны. В алгоритмах типа "Форель" центр тяжести текущего кластера определяется с точностью 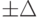 по каждой координате, а порог для включения точки в кластер (радиус шара
по каждой координате, а порог для включения точки в кластер (радиус шара 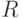 ) из-за погрешностей исходных данных может измениться согласно (74) на
) из-за погрешностей исходных данных может измениться согласно (74) на

Поэтому кроме расчетов с 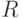 рекомендуется провести также расчеты с радиусами
рекомендуется провести также расчеты с радиусами 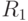 и
и 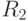 , где
, где