НОУ ИНТУИТ | Прикладная статистика. Лекция 6: Оценивание

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 09.11.2009 | Уровень: для всех | Доступ: платный

|

Вам нравится? Нравится 61 студенту

| Поделиться |

Поддержать программу

В прикладной статистике - иные приоритеты. На первом месте - ОШ-оценки, все остальные НАН-оценки, в том числе ОМП, рассматриваются в качестве дополнительных возможностей.

Пример 1. Найдем ОШ-оценки для гамма-распределения с плотностью

$f(x;a,b,c)= \left\{ \begin{aligned} &\frac{1}{\Gamma(a)}(x-c)^{a-1}b^{-a}\exp\left[-\frac{x-c}{b}\right],x\ge c,\\ &0,\;x<c \end{aligned} \right.$

( 8)

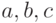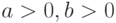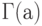Плотность вероятности в формуле (8) определяется тремя параметрами a, b, c , где a>0, b>0 . При этом является параметром формы, - параметром масштаба и - параметром сдвига. Здесь $\Gamma(а)$ - одна из используемых в математике специальных функций, так называемая "гамма-функция", по которой названо и распределение, задаваемое формулой (8),

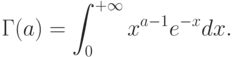
$\Gamma(a)=\int_0^{+\infty}x^{a-1}e^{-x}dx.$

Как следует из явного вида плотности (8), логарифмическая функция правдоподобия имеет вид [ , с.98]:

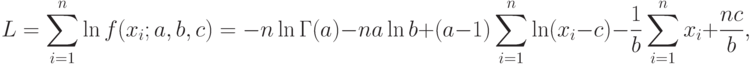
$L=\sum_{i=1}^n\ln f(x_i;a,b,c)=-n\ln\Gamma(a)-na\ln b+ (a-1)\sum_{i=1}^n\ln(x_i-c)-\frac{1}{b}\sum_{i=1}^n x_i+\frac{nc}{b},$

а уравнения правдоподобия таковы:

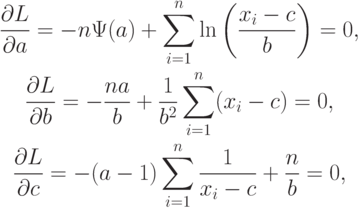
$\begin{gathered} \frac{\partial L}{\partial a}=-n\Psi(a)+\sum_{i=1}^n \ln\left(\frac{x_i-c}{b}\right)=0, \\ \frac{\partial L}{\partial b}=-\frac{na}{b}+\frac{1}{b^2} \sum_{i=1}^n(x_i-c)=0, \\ \frac{\partial L}{\partial c}=-(a-1) \sum_{i=1}^n\frac{1}{x_i-c}+\frac{n}{b}=0, \end{gathered}$

где

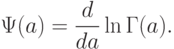
$\Psi(a)=\frac{d}{da}\ln\Gamma(a).$

Ясно, что выписанная система нелинейных уравнений не имеет аналитического решения, в отличие от аналогичной системы для семейства нормальных распределений. Построим ОШ-оценки для задачи оценивания трех неизвестных параметров [

].

В качестве начальных оценок 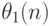$\theta_1(n)$ будем использовать оценки метода моментов (см. 6.1):

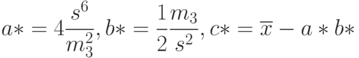
$a*=4\frac{s^6}{m_3^2}, b*=\frac12\frac{m_3}{s^2},c*=\overline{x}-a*b*$

где \overline{x} - выборочное среднее арифметическое, s^2

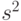- выборочная дисперсия, m^3

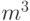- выборочный третий центральный момент.

Матрица информации Фишера согласно [ , с.98] при a > 2 имеет вид

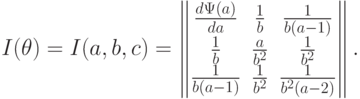$I(\theta)=I(a,b,c)= \begin{Vmatrix} \frac{d\Psi(a)}{da} & \frac{1}{b} & \frac{1}{b(a-1)} \\ \frac{1}{b} & \frac{a}{b^2} & \frac{1}{b^2} \\ \frac{1}{b(a-1)} & \frac{1}{b^2} & \frac{1}{b^2(a-2)} \end{Vmatrix}.$

( 9)

Вектор-столбец частных производных логарифма плотности вероятности

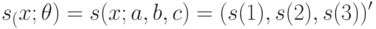
$s_(x;\theta)=s(x;a,b,c)=(s(1),s(2),s(3))'$

имеет координаты

$\begin{gathered} s(1)=-\Psi(a)+\ln\left(\frac{x-c}{b}\right), \\ s(2)=-\frac{a}{b}+\frac{x-c}{b^2}, \\ s(3)=-\frac{a-1}{x-c}+\frac{1}{b}. \end{gathered}$

Таким образом, для получения 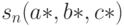s_n(a*, b*, c*) необходимо вычислить две суммы

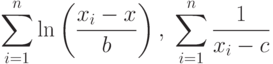
$\sum_{i=1}^n\ln\left(\frac{x_i-x}{b}\right),\;\sum_{i=1}^n\frac{1}{x_i-c}$

и произвести еще несколько арифметических действий, число которых не зависит от объема выборки.

Одношаговые оценки 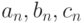a_n, b_n, c_n для параметров гамма-распределения вычисляют по формуле

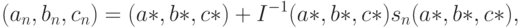
$(a_n, b_n, c_n)=(a*,b*,c*)+I^{-1}(a*,b*,c*)s_n(a*,b*,c*),$

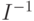где $I^{-1}$ - обратная матрица к матрице информации Фишера

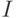, заданной формулой (9). Матрицу 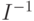$I^{-1}$ нетрудно рассчитать аналитически. Формулы для нахождения одношаговых оценок расписаны в [

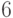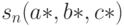]. Расчеты облегчает то обстоятельство, что для гамма-распределения вторая координата вектора s_n(a*, b*, c*)

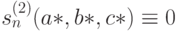тождественно равна 0, т.е. $s_n^{(2)}(a*, b*, c*)\equiv0$ .

При 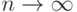$n\rightarrow\infty$ распределение вектора оценок 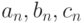a_n, b_n, c_n приближается трехмерным нормальным распределением с математическим ожиданием, равным вектору истинных значений параметров 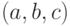(a, b, c) , и ковариационной матрицей 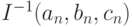$I^{-1}(a_n, b_n, c_n)$ . На этом приближении основаны правила расчета доверительных границ для параметров гамма-распределения [6]. Дисперсии оценок неизвестны, но зато имеются известные статистику зависимости этих дисперсий от параметров гамма-распределения. Эти зависимости непрерывные. Они стоят на главной диагонали ковариационной матрицы 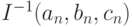$I^{-1}(a_n, b_n, c_n)$ ). Поэтому можно вместо неизвестных параметров подставить в них оценки этих параметров и на основе принципа наследования сходимости (см. "Теоретическая база прикладной статистики" выше) получить состоятельные оценки дисперсий. Затем на основе оценок дисперсий обычным образом строятся доверительные интервалы для параметров гамма-распределения.

В табл.6.4 приведены результаты реализации описанной выше схемы расчетов - точечные и интервальные (при односторонней доверительной вероятности 0,95) оценки параметров гамма-распределения для данных, содержащихся в табл.6.2 предыдущего п. 6.1.

Таблица 6.4. Одношаговые оценки и доверительные границы для параметров гамма-распределения
Параметр	Одношаговая оценка	Верхняя доверительная граница	Нижняя доверительная граница
Формы	7,32	16,41	-1,77
Масштаба	8,77	15,24	2,30
Сдвига	- 11,46	23,28	- 46,20

Приведенные в табл.6.4 данные получены на основе асимптотических формул. Из-за конечности объема выборки необходимо внести некоторые коррективы. Поскольку параметр формы всегда положителен, 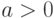a > 0 , то нижняя доверительная граница для этого параметра должна быть неотрицательна, т.е. следует положить 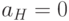a_H = 0 . 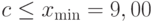Поскольку плотность гамма-распределения положительна только правее параметра , то, очевидно, $c\le x_{\min} = 9,00$ , верхняя доверительная граница для параметра сдвига должна быть заменена на c_B=9,00 .

Может ли параметр сдвига быть отрицательным в данной прикладной задаче? Отрицательность параметра сдвига означает, что с положительной вероятностью рассматриваемая случайная величина отрицательна, т.е. наработка резца до предельного состояния отрицательна. Ясно, что такого быть не может, хотя для специалиста по математической статистике отрицательность параметра сдвига вполне приемлема. Однако специалист по прикладной статистике должен признать неотрицательность параметра с при обработке данных, составляющих рассматриваемую выборку. Следовательно, нижнюю доверительную границу для параметра сдвига необходимо заменить на 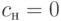c_н = 0 .

Как следует из проведенных выше рассуждений и выкладок (см. также [ , с.98-100]), отношение дисперсий оценок метода моментов и ОШ-оценок имеет вид

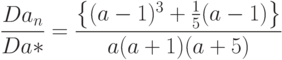
$\frac{Da_n}{Da*}=\frac{\left\{(a-1)^3+\frac15(a-1)\right\}}{a(a+1)(a+5)}$

при больших

. Это отношение, как и должно быть из общих соображений, всегда меньше 1. Отношение дисперсий возрастает при приближении к 0 коэффициента асимметрии распределения. Если a > 39,1

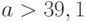(коэффициент асимметрии меньше 0,102), то эффективность оценки метода моментов превышает 80%. При a = 20

(коэффициент асимметрии 0,20) она равна 65%. Напомним, что при безграничном росте параметра формы а гамма-распределение приближается к нормальному, для которого оценки метода моментов и ОМП совпадают, а потому имеют равные дисперсии. Поэтому вполне естественно, что отношение дисперсий в формуле (10) стремится к 1 при безграничном росте параметра формы

.

Хотя дисперсии оценок метода моментов, как правило, больше, чем дисперсии НАН-оценок, таких, как ОШО и ОМП, метод моментов играет большую роль в прикладной статистике. Во-первых, обычно их расчет проще (в частности, требует меньшего числа компьютерных операций), чем оценок других типов. К тому же оценки находятся с помощью выборочных моментов, которые, как правило, вычисляются на этапе описания статистических данных. Во-вторых, они служат основой для вычисления оценок других типов, например, ОШО. Для запуска итерационных методов нахождения ОМП также нужны начальные значения, и ими обычно являются оценки метода моментов. В-третьих, при учете погрешностей результатов наблюдений оценки метода моментов могут оказаться точнее ОМП и асимптотически эквивалентных им ОШО (см. "Статистика интервальных данных" настоящего курса).

Методы оценивания параметров гамма-распределения и примеры расчетов для всех семи постановок, перечисленных в табл.6.1 п.6.1, приведены в [ [ 6.6 ] ]. Большинство из них основано на асимптотических (при 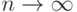$n\rightarrow\infty$ ) теоретических результатах прикладной статистики. Методом статистических испытаний (Монте-Карло) показано, что уже при $n\ge 10$ используемые приближения удовлетворительны. Другими словами, асимптотической нормальностью оценок и другими важными для проведенных выше рассуждений предельными результатами можно пользоваться уже при $n\ge 10$ .

Алгоритмическое и программное обеспечение ОШ-оценок для распределения Вейбулла-Гнеденко и гамма-распределения рассмотрено в монографии [ [ 6.21 ] ]. История вопроса освещена в статье [ [ 2.14 ] ].

Дальше >>

Прикладная статистика

Прикладная статистика

Оценивание

Вопросы и ответы

Студенты

Авторизоваться

Прикладная статистика

Прикладная статистика

Оценивание

Вопросы и ответы

Студенты