|
Здравствуйте! 4 июня я записалась на курс Прикладная статистика. Заплатила за получение сертификата. Изучала лекции, прошла Тест 1. Сегодня вижу, что я вне курса! Почему так произошло? |
Оценивание
6.2. Одношаговые оценки
Одношаговые оценки имеют столь же хорошие асимптотические свойства, что и оценки максимального правдоподобия, при тех же условиях регулярности, что и ОМП. Грубо говоря, они представляют собой результат первой итерации при решении системы уравнений максимального правдоподобия по методу Ньютона-Рафсона. Одношаговые оценки выписываются в виде явных формул, а потому требуют существенно меньше машинного времени, а также могут применяться при ручном счете (на калькуляторах). Снимаются вопросы о сходимости алгоритмов, о выборе момента прекращения вычислений, о влиянии округлений при вычислениях на окончательный результат. ОШ-оценки были использованы нами при разработке ГОСТ 11.011-83 вместо ОМП.
Как и раньше, рассмотрим выборку 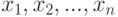 из распределения с плотностью
из распределения с плотностью 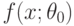 , где
, где 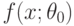 - элемент параметрического семейства плотностей распределения вероятностей
- элемент параметрического семейства плотностей распределения вероятностей 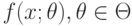 . Здесь
. Здесь  - известное статистику k-мерное пространство параметров, являющееся подмножеством евклидова пространства Rk, а конкретное значение параметра ?0 неизвестно. Его и будем оценивать.
- известное статистику k-мерное пространство параметров, являющееся подмножеством евклидова пространства Rk, а конкретное значение параметра ?0 неизвестно. Его и будем оценивать.
Обозначим 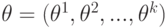 . Рассмотрим вектор-столбец частных производных логарифма плотности вероятности
. Рассмотрим вектор-столбец частных производных логарифма плотности вероятности


Положим
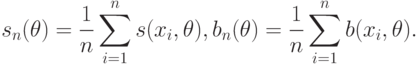
Пусть матрица информации Фишера ![I(\theta_0)=M[-b_n(\theta_0)]](/sites/default/files/tex_cache/10aa2c8dedd703e8aa45c8fc29d8abf9.png) положительно определена.
положительно определена.
Определение 1 [
[
6.7
]
, с.269]. Оценку 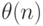 параметра
параметра 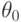 называют наилучшей асимптотически нормальной оценкой (сокращенно НАН-оценкой), если распределение случайного вектора
называют наилучшей асимптотически нормальной оценкой (сокращенно НАН-оценкой), если распределение случайного вектора 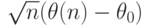 сходится при
сходится при 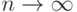 к нормальному распределению с нулевым математическим ожиданием и ковариационной матрицей, равной
к нормальному распределению с нулевым математическим ожиданием и ковариационной матрицей, равной 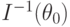 .
.
Определение 1 корректно: 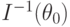 является нижней асимптотической границей для ковариационной матрицы случайного вектора
является нижней асимптотической границей для ковариационной матрицы случайного вектора 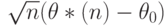 , где
, где 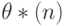 - произвольная оценка; ОМП - это НАН-оценки (см. [
[
6.7
]
] и др.). Некоторые другие оценки также являются НАН-оценками, например, байесовские. Сказанное об ОМП и байесовских оценках справедливо при некоторых условиях регулярности (см., например, [
[
4.7
]
]). В ряде случаев несмещенные оценки являются НАН-оценками, более того, они лучше, чем ОМП (их дисперсия меньше), при конечных объемах выборки [
[
6.13
]
].
- произвольная оценка; ОМП - это НАН-оценки (см. [
[
6.7
]
] и др.). Некоторые другие оценки также являются НАН-оценками, например, байесовские. Сказанное об ОМП и байесовских оценках справедливо при некоторых условиях регулярности (см., например, [
[
4.7
]
]). В ряде случаев несмещенные оценки являются НАН-оценками, более того, они лучше, чем ОМП (их дисперсия меньше), при конечных объемах выборки [
[
6.13
]
].
Для анализа реальных данных естественно рекомендовать какую-либо из НАН-оценок. (Это утверждение всегда верно на этапе асимптотики при изучении конкретной задачи прикладной статистики. Теоретически можно предположить, что при тщательном изучении для конкретных конечных объемов выборки наилучшей окажется какая-либо оценка, не являющаяся НАН-оценкой. Однако такие ситуации нам пока не известны.)
Пусть  и
и 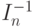 - некоторые оценки
- некоторые оценки 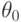 и
и 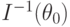 соответственно.
соответственно.
Определение 2. Одношаговой оценкой (ОШ-оценкой, или ОШО) называется оценка
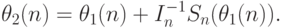
Теорема 1 [ [ 2.14 ] ]. Пусть выполнены следующие условия.
(I) Распределение  сходится при
сходится при 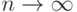 к нормальному распределению с математическим ожиданием 0 и ковариационной матрицей
к нормальному распределению с математическим ожиданием 0 и ковариационной матрицей  и, кроме того, существует
и, кроме того, существует 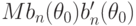 .
.
(II) При некотором 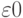 и
и 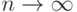

(III) Для любого 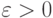
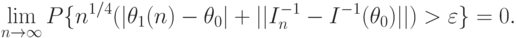
Тогда ОШ-оценка является НАН-оценкой.
Доказательство. Рассмотрим тождество
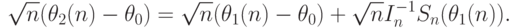 |
( 1) |
В силу условия (II) теоремы
 |
( 2) |
Из условия (I) теоремы следует, что первое слагаемое в правой части формулы (2) сходится при 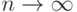 по распределению к нормальному закону с математическим ожиданием 0 и ковариационной матрицей
по распределению к нормальному закону с математическим ожиданием 0 и ковариационной матрицей 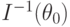 . Согласно условию (III)
. Согласно условию (III)
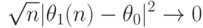
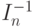 ограничена по вероятности. Поэтому третье слагаемое в правой части формулы (2) сходится к 0 по вероятности. Для завершения доказательства теоремы осталось показать, что
ограничена по вероятности. Поэтому третье слагаемое в правой части формулы (2) сходится к 0 по вероятности. Для завершения доказательства теоремы осталось показать, что |
( 3) |
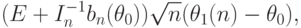 |
( 4) |
 - единичная матрица. Поскольку из условия (I) теоремы следует, что для
- единичная матрица. Поскольку из условия (I) теоремы следует, что для 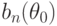 справедлива (многомерная) центральная предельная теорема, то
справедлива (многомерная) центральная предельная теорема, то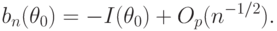
С учетом условия (III) теоремы заключаем, что
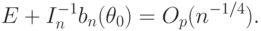 |
( 5) |
Из соотношений (4), (5) и условия (III) теоремы вытекает справедливость формулы (3). Теорема доказана.
Прокомментируем условия теоремы. Условия (I) и (II) обычно предполагаются справедливыми при рассмотрении оценок максимального правдоподобия [
[
6.7
]
]. Эти условия можно выразить в виде требований, наложенных непосредственно на плотность  из параметрического семейства, как это сделано, например, в [
[
4.7
]
]. Условие (III) теоремы, наложенное на исходные оценки, весьма слабое. Обычно используемые оценки
из параметрического семейства, как это сделано, например, в [
[
4.7
]
]. Условие (III) теоремы, наложенное на исходные оценки, весьма слабое. Обычно используемые оценки  и
и 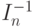 являются не
являются не  -состоятельными, а
-состоятельными, а  -состоятельными, т.е. условие (III) заведомо выполняется.
-состоятельными, т.е. условие (III) заведомо выполняется.
Какие оценки годятся в качестве начальных? В качестве 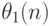 можно использовать оценки метода моментов, как это сделано в ГОСТ 11.011-83 [
[
6.6
]
], или, например, квантильные. В качестве
можно использовать оценки метода моментов, как это сделано в ГОСТ 11.011-83 [
[
6.6
]
], или, например, квантильные. В качестве 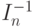 в теоретической работе [
[
6.7
]
] предлагается использовать простейшую оценку
в теоретической работе [
[
6.7
]
] предлагается использовать простейшую оценку
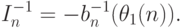 |
( 6) |
Для гамма-распределения с неизвестными параметрами формы, масштаба и сдвига ОШ-оценки применены в [
[
6.6
]
]. При этом оценка (6) оказалась непрактичной, поскольку с точностью до погрешностей измерений и вычислений 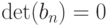 для реальных данных о наработке резцов до предельного состояния, приведенных выше в табл.6.2 (п.6.1). Поскольку
для реальных данных о наработке резцов до предельного состояния, приведенных выше в табл.6.2 (п.6.1). Поскольку 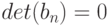 , то обратная матрица не существует, вычисления по формуле (6) невозможны. Поэтому в [
[
6.6
]
] в качестве ОШ-оценки была применена непосредственно первая итерация метода Ньютона-Рафсона решения системы уравнений максимального правдоподобия, т.е. была использована оценка
, то обратная матрица не существует, вычисления по формуле (6) невозможны. Поэтому в [
[
6.6
]
] в качестве ОШ-оценки была применена непосредственно первая итерация метода Ньютона-Рафсона решения системы уравнений максимального правдоподобия, т.е. была использована оценка
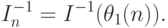 |
( 7) |
В формуле (7) непосредственно используется явный вид зависимости матрицы информации Фишера от неизвестных параметров распределения.
В других случаях выбор тех или иных начальных оценок, в частности, выбор между (6) и (7), может определяться, например, простотой вычислений. Можно использовать также устойчивые аналоги [ [ 1.15 ] ] перечисленных выше оценок.
Необходимо отметить, что еще в 1925 г., т.е. непосредственно при разработке метода максимального правдоподобия, его создатель Р.Фишер считал, что первая итерация по методу Ньютона-Рафсона дает хорошую оценку вектору неизвестных параметров [ [ 6.7 ] , с.298]. Он однако рассматривал эту оценку как аппроксимацию ОМП. А.А. Боровков воспринимает ОШ-оценки как способ "приближенного вычисления оценок максимального правдоподобия" [ [ 6.2 ] , с.225] и показывает асимптотическую эквивалентность ОШ-оценок и ОМП (в более сильных предположениях, чем в теореме 1; другими словами, теорема 1 обобщает результаты А.А. Боровкова относительно ОШ-оценок). Мы же полагаем, что ОШ-оценки имеют самостоятельную ценность, причем не меньшую, а в ряде случаев большую, чем ОМП. По нашему мнению, ОМП целесообразно применять (на этапе асимптотики) только тогда, когда они находятся явно. Во всех остальных случаях следует использовать на этом этапе ОШ-оценки (или какие-либо иные, выбранные из дополнительных соображений).
С чем связана популярность оценок максимального правдоподобия? Из всех НАН-оценок они наиболее просто вводятся и ранее других предложены. Поэтому среди математиков сложилась устойчивая традиция рассматривать ОМП в курсах математической статистики. Однако при этом игнорируются вычислительные вопросы, а также отодвигаются в сторону многочисленные иные НАН оценки.

