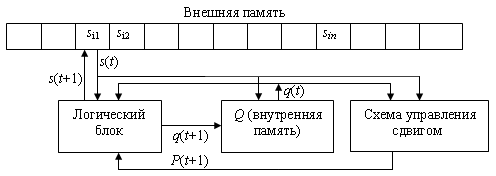
Структура однопрограммной ЭВМ
Классические основы построения ЭВМ
Основы построения электронных вычислительных машин в их современном понимании были заложены в 30-е – 40-е годы прошлого века видными учеными: английским математиком Аланом Тьюрингом и американцем венгерского происхождения Джоном (Яношем) Нейманом.
Машина Тьюринга
В 1936 году А. Тьюринг сформулировал понятие абстрактной вычислительной машины. Одновременно с ним, хотя и не в столь явной форме, это же сделал Э. Пост (США). Хотя машина Тьюринга (МТ) не стала реально действующим устройством, она до настоящего времени постоянно используется в качестве основной модели для выяснения сущности таких понятий, как "вычислительный процесс", "алгоритм", а также для выяснения связи между алгоритмом и вычислительными машинами [ 11 ] .
Основные положения машины Тьюринга
-
Машина Тьюринга (рис.10.1) имеет конечное число знаков si, образующих внешний алфавит, в котором кодируются сведения, подаваемые в МТ, а также вырабатываемые в ней. Среди знаков имеется пустой знак ( s1 ), посылка которого в какую-либо ячейку стирает находившийся в ней знак и оставляет ее пустой.
В зависимости от поданной начальной информации
 (содержащихся на ленте внешней памяти знаков) возможны два случая:
(содержащихся на ленте внешней памяти знаков) возможны два случая:- после конечного числа тактов машина останавливается (имея информацию
 ), подавая сигнал об остановке. В этом случае МТ применима к информации
), подавая сигнал об остановке. В этом случае МТ применима к информации  и перерабатывает ее в информацию
и перерабатывает ее в информацию  ;
; - остановка никогда не наступает. В этом случае МТ не применима к начальной информации
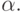
- после конечного числа тактов машина останавливается (имея информацию
-
В каждый момент обозревается лишь одна ячейка ленты (памяти). Переход может осуществляться лишь к соседней ячейке ( R – вправо, L –влево, N – нет перехода (остаться)). Переход к произвольной ячейке производится путем последовательного перебора всех ячеек, разделяющих текущую и необходимую ячейки. На каждом отдельном такте t команда предписывает только замену единственного знака si, хранящегося в обозреваемой ячейке, каким-либо другим знаком sj.
-
Логический блок МТ имеет конечное число состояний {qi} i=1..m.
Знаки R, L, N, q1,.., qm образуют внутренний алфавит машины.
Переработанный знак sj, записываемый в просматриваемую ячейку, состояние, которое примет машина Тьюринга в следующем такте q(t+1) и выполняемая в данном такте операция перехода к следующей ячейке P(t+1) являются функцией анализируемого в данном такте символа и текущего состояния машины si и q(t):
si(t+1)=f1(si,q(t)); q(t+1)=f2(si,q(t)); P(t+1)=f3(si,q(t)).
Программа для МТ определяется тройкой {si, P, q}t.
Пример записи программы вычисления логической функции "неравнозначность" для машины Тьюринга представлен ниже.
Символ ( si ) Состояние q1 q2 q3 q4 0 0, R, q2 0, N, q4 1, N, q4 0, N, q4 1 1, R, q3 1, N, q4 0, N, q4 1, N, q4 Перед началом работы машина Тьюринга находится в состоянии q1 считывания первого операнда.
Данная МТ применима к исходной информации. Останов – состояние q4. Значение si в ячейке y не меняется (сохраняется результат).
Если программа для МТ будет определена таблицей переходов
Символ ( si ) Состояние q1 q2 q3 q4 0 0, R, q2 0, N, q4 1, N, q4 1, N, q4 1 1, R, q3 1, N, q4 0, N, q4 0, N, q4 то данная МТ будет не применима к исходной информации, поскольку в состоянии q4 значение si в ячейке y постоянно меняется на противоположное.
Автомат Неймана
По принципу обработки информации вычислительное устройство, предложенное Нейманом ( автомат Неймана – АН), существенно отличается от машины Тьюринга.
Важная особенность машины Тьюринга – преобразование информации на каждом такте происходит лишь в одной ячейке, остальные дожидаются посещения головки, хотя часто имеется возможность работать параллельно.
Простейшее решение – использование нескольких машин Тьюринга с общей для них внешней памятью (лентой) – не всегда допустимо из-за возможных конфликтов при обращении к одной и той же ячейке памяти.
В автомате Неймана число одновременно обрабатываемых ячеек может неограниченно расти, оставаясь в каждый момент конечным.
Элемент Неймана (ЭН) – это устройство, которое на каждом такте пребывает в одном из конечного числа состояний 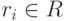 , образующих его алфавит. ЭН имеет два входных канала: левый и правый; по каждому из них на такте t также поступает по одному состоянию из R (рис. 2).
, образующих его алфавит. ЭН имеет два входных канала: левый и правый; по каждому из них на такте t также поступает по одному состоянию из R (рис. 2).
Элемент реализует функцию 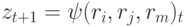 , то есть в такте t+1 переходит в состояние z, определяемое его состоянием в текущий момент времени и значениями, поступившими по входным каналам.
, то есть в такте t+1 переходит в состояние z, определяемое его состоянием в текущий момент времени и значениями, поступившими по входным каналам.
Состояния элементов Неймана в момент времени t определяют конфигурацию автомата Неймана (рис. 3) в момент t: K(t).
Функционирование АН – это переход от состояния К(t) к состояниям K(t+1), K(t+2)...
За один такт свое состояние может менять большое число элементов Неймана, что фактически приводит к параллельной обработке информации.