Основные семейства распределений
Примеры абсолютно непрерывных распределений
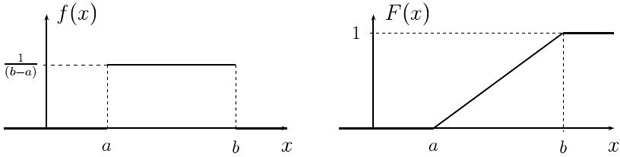
Равномерное
распределение.
Говорят, что  имеет
равномерное распределение на отрезке
имеет
равномерное распределение на отрезке ![[a,\,b]](/sites/default/files/tex_cache/d2524b9940ce1c636bfb26ae09a941d2.png) , и пишут:
, и пишут: 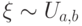 ,
если плотность распределения
,
если плотность распределения  постоянна на отрезке
постоянна на отрезке ![[a,\,b]](/sites/default/files/tex_cache/d2524b9940ce1c636bfb26ae09a941d2.png) и равна нулю вне него:
и равна нулю вне него:
![f_\xi(x)=\begin{cases}
\frac{1}{b-a}, & \textrm{\, если\, } x\in[a,\,b], \cr
\,0, & \textrm{\, если\, } x\not\in[a,\,b].
\end{cases}](/sites/default/files/tex_cache/8f75b7256945dfe9b9fa4951e85f533e.png)
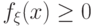 .
Поэтому
.
Поэтому 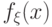 является плотностью распределения.
является плотностью распределения.Случайная величина 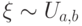 имеет
смысл координаты точки, выбранной наудачу на отрезке
имеет
смысл координаты точки, выбранной наудачу на отрезке ![[a,\,b]](/sites/default/files/tex_cache/d2524b9940ce1c636bfb26ae09a941d2.png) .
Вычислим функцию
распределения случайной величины
.
Вычислим функцию
распределения случайной величины  :
:
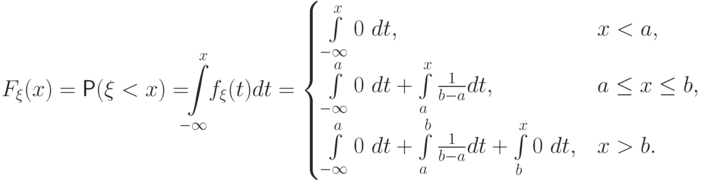
![[a, b]](/sites/default/files/tex_cache/022022f289db140169cd9514f74ee648.png) изображены на
рис.
7.1
изображены на
рис.
7.1Заметьте, что в точках 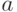 и
и  функция распределения
недифференцируема,
и плотность можно задать как угодно.
функция распределения
недифференцируема,
и плотность можно задать как угодно.
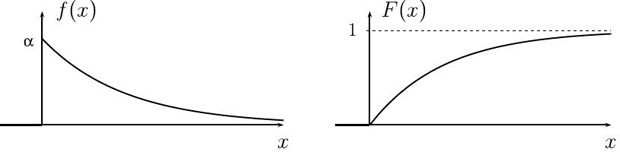
Показательное распределение.
Говорят, что  имеет
показательное (экспоненциальное) распределение с параметром
имеет
показательное (экспоненциальное) распределение с параметром 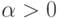 ,
и пишут:
,
и пишут: 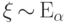 ,
если
,
если  имеет следующую плотность распределения:
имеет следующую плотность распределения:
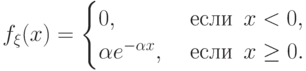
 непрерывна:
непрерывна: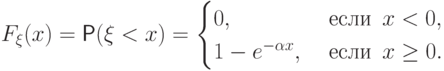
Графики плотности и функции распределения показательного распределения
с параметром  приведены на
рис.
7.2
приведены на
рис.
7.2
Плотность показательного распределения
равна нулю на отрицательной полуоси, поэтому
вероятность события 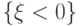 нулевая -
случайная величина с показательным распределением не может быть
отрицательна.
К тому же плотность отлична от нуля на всей положительной полуоси,
поэтому случайная величина с показательным распределением может принимать
сколь угодно большие положительные значения: для всякого
нулевая -
случайная величина с показательным распределением не может быть
отрицательна.
К тому же плотность отлична от нуля на всей положительной полуоси,
поэтому случайная величина с показательным распределением может принимать
сколь угодно большие положительные значения: для всякого 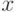 вероятность
события
вероятность
события 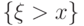 не равна нулю.
не равна нулю.
Показательное распределение является единственным абсолютно непрерывным распределением, для которого выполнено свойство "нестарения" (и в этом смысле оно является непрерывным аналогом дискретного геометрического распределения).
Теорема 23.
Пусть 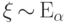 . Тогда для любых
. Тогда для любых 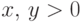
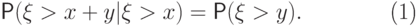 |
( 7.1) |
Нормальное
распределение.
Говорят, что  имеет
нормальное (гауссовское) распределение с параметрами
имеет
нормальное (гауссовское) распределение с параметрами 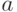 и
и  , где
, где 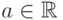 ,
,  ,
и пишут:
,
и пишут:  ,
если
,
если  имеет следующую плотность распределения:
имеет следующую плотность распределения:
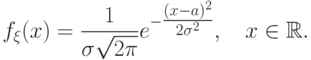
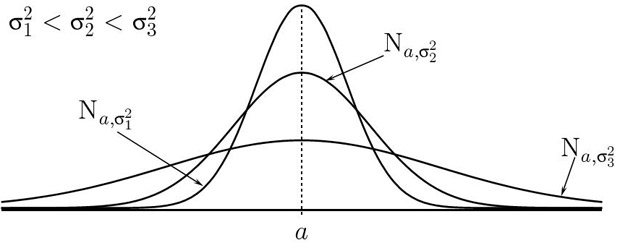
На
рис.
7.3 приведены графики плотностей нормальных распределений с одним
и тем же параметром 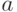 и разными значениями параметра
и разными значениями параметра 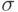 .
.
Убедимся, что 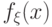 является плотностью распределения.
Так как
является плотностью распределения.
Так как 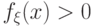 для всех
для всех 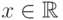 , то свойство
(f1) выполнено.
Проверим (f2):
, то свойство
(f1) выполнено.
Проверим (f2):
![\begin{multiple}
\int\limits_{-\infty}^\infty f_\xi(x)\,dx&=&
\int\limits_{-\infty}^\infty \frac{1}{\sigma\sqrt{2\pi}}~
e^{-\tfrac{(x-a)^2}{2\sigma^2}}\,dx=
\left[\begin{array}{c}\text{ замена переменных } \cr
t=\frac{x-a}{\sigma}, \, dx=\sigma\,dt
\end{array}\right]\, =\\\int\limits_{-\infty}^\infty \frac{1}{\sigma\sqrt{2\pi}}~
e^{-t^2/2}\sigma\,dt=
\frac{1}{\sqrt{2\pi}}~ \int\limits_{-\infty}^\infty
e^{-t^2/2}\,dt\,=\frac{I}{\sqrt{2\pi}}\,=1,
\end{multiple}](/sites/default/files/tex_cache/3646667ecbc72435575b4d3bb31c0260.png)
 обозначен табличный интеграл (интеграл
Пуассона)
обозначен табличный интеграл (интеграл
Пуассона)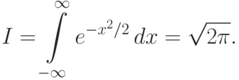
Нормальное распределение 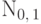 с параметрами
с параметрами 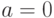 и
и 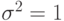 называется
стандартным нормальным распределением.
Плотность стандартного нормального распределения равна
называется
стандартным нормальным распределением.
Плотность стандартного нормального распределения равна 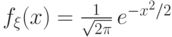 .
.
Мы будем использовать специальное обозначение 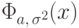 для функции распределения нормального закона
для функции распределения нормального закона 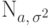 (
рис.
7.3).
Первообразная функции
(
рис.
7.3).
Первообразная функции 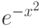 не может быть выражена
через
элементарные функции. Поэтому функцию
не может быть выражена
через
элементарные функции. Поэтому функцию 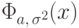 можно записать лишь в виде интеграла
можно записать лишь в виде интеграла
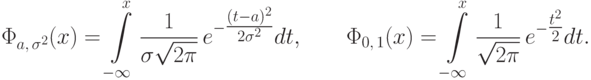
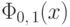 табулирована, т.е. ее значения
при различных вещественных
табулирована, т.е. ее значения
при различных вещественных 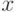 вычислены.
Их можно найти в соответствующих таблицах.
вычислены.
Их можно найти в соответствующих таблицах.