Первое знакомство с пакетом Mathematica
Специальные операции над списками
![\tt
In[87]:=\{1,2,3\} . \{x,y,z\} \\ \\
Out[87]=x+2y+3z \\ \\
In[88]:= \{\{a,b\},\{c,d\}\} . \{x,y\} \\ \\
Out[88]=\{ax+by, cx+dy\}](/sites/default/files/tex_cache/bc4afb952fac75dd21b37d7f1903b677.png)
Список 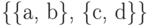 представляет собой матрицу и может быть визуализирован в привычной форме
представляет собой матрицу и может быть визуализирован в привычной форме
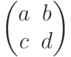 с использованием палетки (
с использованием палетки ( ):
):
![\tt
In[89]:=
\begin{pmatrix}
a&b\\
c&d
\end{pmatrix} \cdot \{x,y\}}\\ \\
Out[89]=\{ax+by, cx+dy\}\\ \\
In[90]:= \begin{pmatrix}
a&b\\
c&d
\end{pmatrix} \cdot \begin{pmatrix}
x&y\\
z&t
\end{pmatrix}}\\ \\
Out[90]=\{\{ax+bz, bt+ay\}, \{cx+dz, dt + cy\}\}](/sites/default/files/tex_cache/3b258143fb25bfb1681f0273a9e76292.png)
Чтобы вывести список в матричной форме, можно использовать команду
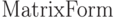
![\tt
In[91]:= \begin{pmatrix}
a&b\\
c&d
\end{pmatrix}.
\begin{pmatrix}
x&y\\
z&t
\end{pmatrix}// MatrixForm\\ \\
Out[91]=\begin{pmatrix}
ax+bz&bt+ay\\
cx+dz&dt+cy
\end{pmatrix}](/sites/default/files/tex_cache/12adb83a14083b1fd83af230d6c26041.png)
Применение функций к спискам
Функция 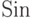 , примененная к списку, вычисляется на каждом элементе списка (функции, обладающие таким свойством, называются
, примененная к списку, вычисляется на каждом элементе списка (функции, обладающие таким свойством, называются  ):
):
![\tt
In[92] := Sin[\{l, 2, 3, 4, 5\}] \\ \\
Out[92] = \{Sin [1] , Sin[2], Sin[3], Sin[4], Sin[5]\}](/sites/default/files/tex_cache/5c33919cb0ee1ec97a4d5cf9805ae033.png)
Не всякая функция является  :
:
![\tt
In[93]:= f [\{1, 2, 3, 4, 5\}] \\ \\
Out[93] = f [\{1, 2, 3, 4, 5\}]](/sites/default/files/tex_cache/0821f0f6c995c69f7c9f57e354f2081b.png)
Чтобы применить функцию  , не являющуюся
, не являющуюся  , к списку
, к списку 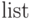 , можно воспользоваться командой
, можно воспользоваться командой ![\text{Map[f, list]}](/sites/default/files/tex_cache/8388864f5e1a48bae25728a6b1a0984b.png) :
:
![\tt
In[94]: = Map[f,\{1, 2, 3, 4, 5\}]
Out[94]=\{f [1], f[2], f[3], f[4], f[5]\}](/sites/default/files/tex_cache/717e70f202cda00728ff702ab4d7f8e7.png)
Функцию  удобно задавать непосредственно внутри команды
удобно задавать непосредственно внутри команды  , не присваивая ей имени:
, не присваивая ей имени:
![\tt
In[95]:= Map[\#^2 \&, \{1, 2, 3, 4, 5\}] \\ \\
Out[95] = \{1, 4, 9, 16, 25\}](/sites/default/files/tex_cache/db7a9eef7984fe4182651e8911334459.png)
Чтобы применить функцию  нескольких переменных к набору списков, нужна команда
нескольких переменных к набору списков, нужна команда ![\text{\tt MapThread[f, \{list1, list2, \ldots \}]}](/sites/default/files/tex_cache/713b961589a17bb1fc537a1cc6d7ac14.png) :
:
![\tt
In[96]:= MapThread[\#1^2 - \#2^3 &, \{\{1, 2, 3\}, \{x, у, z\}\} \\ \\
Out[96] = \{1 - x^3, 4-y^3, 9-z^3\}](/sites/default/files/tex_cache/3f550cb87c851ea4f43d747e9e214908.png)
Создание списков
Следующая команда задает список от 1 до 17 с шагом 2:
![\tt
In[97]:= Table[k, \{k, 1, 17, 2\}] \\ \\
Out[97]=\{1, 3, 5, 7, 9, 11, 13, 15, 17\}](/sites/default/files/tex_cache/da56f2136433338e24ddd2279a804fa2.png)
Следующая команда задает матрицу из трех строк ( - номер строки) длины 5 (элементы строки нумеруются
- номер строки) длины 5 (элементы строки нумеруются 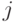 ), в которой
), в которой 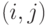 -й элемент имеет вид
-й элемент имеет вид 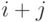 :
:
![\tt
In[98]:= Table [i + j, \{i, 1, 3\}, \{j, 1, 5\}] \\ \\
Out[98] =\{\{2, 3, 4, 5, 6\}, \{3, 4, 5, 6, 7\}, \{4, 5, 6, 7, 8\}\}](/sites/default/files/tex_cache/a01f18cd4131a7974bafa98e56eecdd6.png)
Следующая команда создает список натуральных чисел от 1 до 5:
![\tt
In[99]: = Range [5] \\ \\
Out[99] = {1, 2, 3, 4, 5}](/sites/default/files/tex_cache/aa606850503b89e9962279924a9edb8c.png)
Следующая команда объединяет списки:
![\tt
In[100]:=Join[ \{ 1, 2, 3\} , \{ 3, 4, 5\} ] \\
\phantom{In[100]:=}\,\{1, 2, 3\} \sim Join \sim \{ 3, 4, 5\} \\ \\
Out[100]=\{ 1, 2, 3, 3, 4, 5\} \\ \\
Out[101]= \{ 1, 2, 3, 3, 4, 5\}](/sites/default/files/tex_cache/23613470e64454f045ae1e0f7ad559c4.png)
Следующая команда объединяет подсписки в единый список (убирает внутренние фигурные скобки):
![\tt
In[102]:= \begin{pmatrix}
1&2\\
3&4
\end{pmatrix}}\\
\phantom{In[102]:=}\,Flatten
\begin{matrix}
\left [ \begin{pmatrix}
1&2\\
3&4
\end{pmatrix} \right ]}
\end{matrix} \\ \\
Out[102]=\{\{1,2\}, \{3,4\}\} \\ \\
Out[103]=\{1,2,3,4\}](/sites/default/files/tex_cache/f60dfb132c38aeb44e51a5940c6a7bb4.png)
Следующая функция создает список из последовательных непересекающихся подсписков длины 3:
![\tt
In[104]:= Partition[\{a,b,c,d,e,f,g\},3] \\ \\
Out[104]=\{\{a,b,c\}, \{d,e,f\}\} \\ \\
In[105]:=m=\{\{1,2,3\}, \{4,5,6\}, \{7,8,9\}\}; \\
\phantom{In[105]:=}\;m// MatrixForm \\
\phantom{In[105]:=}\;Transpose[m] // MatrixForm \\ \\
Out[106]=\begin{pmatrix}
1&2&3\\
4&5&6\\
7&8&9
\end{pmatrix}\\ \\
Out[107]=\begin{pmatrix}
1&4&7\\
2&5&8\\
3&6&9
\end{pmatrix}](/sites/default/files/tex_cache/65a9b48a227c1265b511ef43b3640228.png)
Некоторые графические возможности
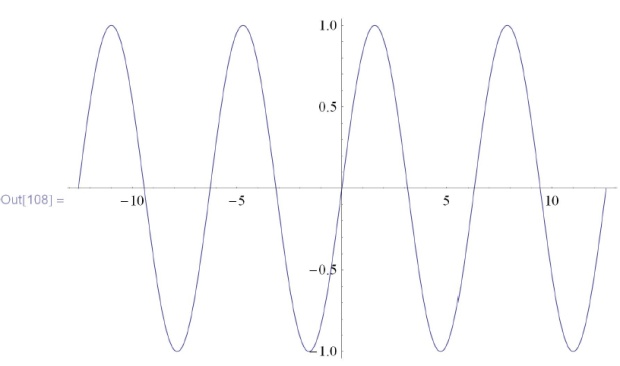
![\tt
In[108]:=Plot [Sin [x], \{ x, -4\pi, 4\pi \}]](/sites/default/files/tex_cache/3a320b675ce289cc4dc366d19ac9b825.png)
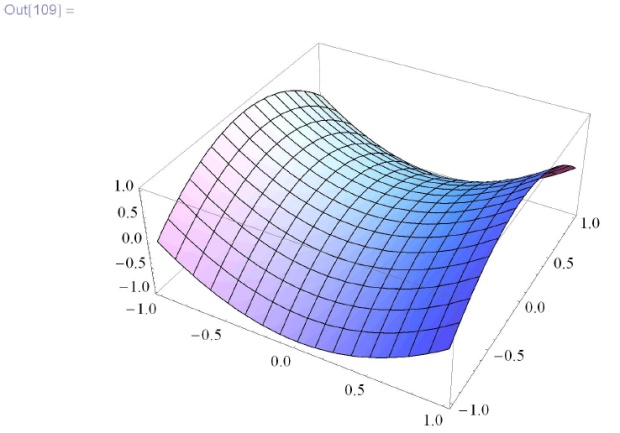
![\tt
In[109]:= Plot3D[x\^\,\!2 - у\^\,\!2, \{х,-1,1\},\{у, -1, 1\}] \\ \\](/sites/default/files/tex_cache/f9dc803262721498e6e67690c86e5577.png)
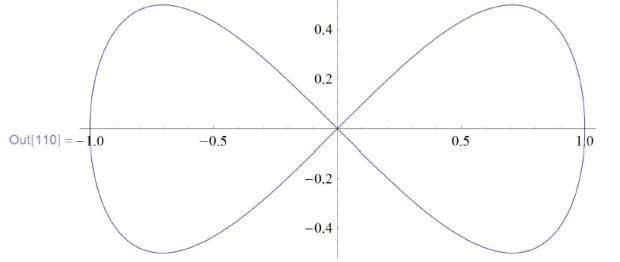
![\tt
In[110]:= ParametricPlot[\{Cos[t], Sin[t] Cos [t] \}, \{t, 0, 2\pi \}]](/sites/default/files/tex_cache/54f131149c19bd2e1e815eb0d155a73e.png)
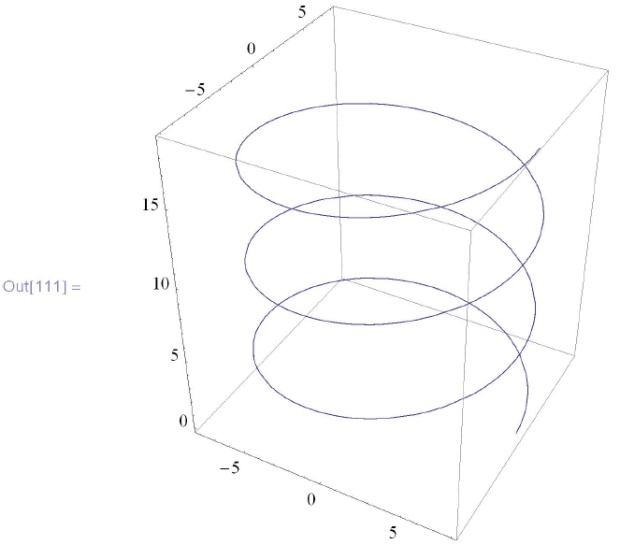
![\tt
In[111]:= ParametricPlot3D[\{ 8 Cos[t] , 8 Sin[t], t\} , \{ t, 0, 6\pi \}]](/sites/default/files/tex_cache/fc8ebc25470bbeb4c8dcf32945097fd8.png)
![\tt
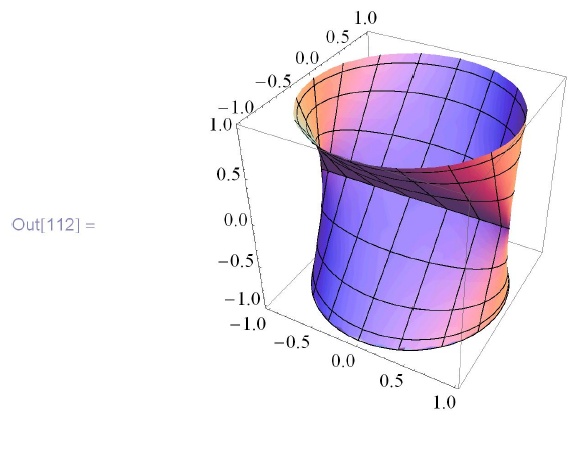
In[112]:=ParametricPlot3D [\{ Cos [u] , Sin[u] Cos [v] , Cos [v] \}, \\
\phantom{In[112]:=P}\!\{u,0,2\pi\}, \{v,0,2\pi\}]](/sites/default/files/tex_cache/3eaf1d1dfce9c4522bc221c8a77bfbc2.png)