Отладка параллельной программы с использованием Intel Thread Checker

11.2.4. Задача о роботе

11.2.4.1. Постановка задачи

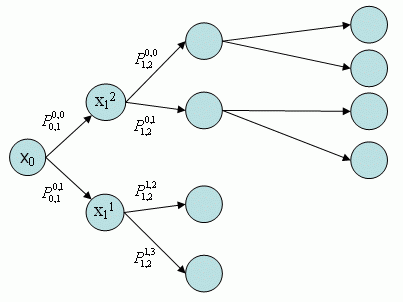
Для постановки задачи рассмотрим некоторую "гипотетическую" лабораторию искусственного интеллекта, в которой выполняются работы по созданию роботов.

Для испытаний лабораторных образцов построен полигон, устроенный следующим образом: в начале полигона находится единственная дверь. Пройдя через нее, робот оказывается перед дверьми. Выбрав одну из дверей, робот вновь оказывается перед дверьми, и т.д. Пройдя через дверь, робот получает премию в размере , где - количество монет, лежащее за данной дверью (для разных дверей количество монет может быть разным).

Считая известным:

• количество дверей ( ),
• количество уровней полигона ( ),
• количество монет лежащее за дверью на уровне 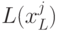и
• вероятности выбора роботом, находящемся за дверью на уровне ,двери 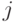на уровне ,

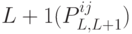следует определить среднюю премию, получаемую роботом при проходе через данный полигон.

Считать, что выполняются следующие условия:

11.2.4.2. Модель

Объектом исследования в данной задаче является полигон с иерархической структурой, по которому по определенному алгоритму перемещается робот. Построим математическую модель исследуемого объекта.

Прежде всего, введем необходимые обозначения.

• - количество вариантов пути, выбираемых роботом на каждом шаге.
• - количество уровней полигона.
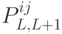• - вероятность попадания из узла уровня в узел 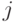уровня .
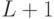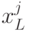• - количество монет, лежащее за дверью уровня .

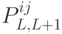  , , и 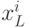являются исходными данными для данной задачи. Из условия задачи вытекают следующие ограничения на исходные данные:
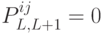• , если двери и 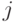не соединены.
• .

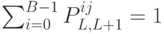Теперь перейдем непосредственно к выбору модели. Вследствие иерархической структуры полигона выглядит разумным его представление в виде дерева степени и глубины . При этом узлы дерева содержат значения 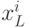, а дугам приписаны вероятности перехода .

Рис. 11.18. Модель полигона в задаче о роботе

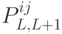11.2.43. .Метод решения

Перейдем к описанию метода нахождения результата. Пусть 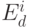- средняя премия, которая может быть получена, если робот начинает путь в узле уровня .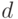

Тогда

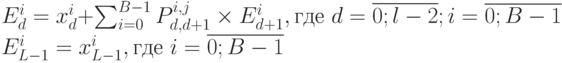
Очевидный метод вычисления результата 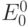состоит в вычислении значений 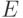на последнем уровне дерева (второе соотношение) с последующим пересчетом из конца в начало (первое рекуррентное соотношение).

11.2.4.4. Последовательная реализация

Перейдем к реализации последовательной версии изложенного выше метода решения.

Проектирование структур данных

Предусмотрим для представления дерева константы, хранящие степень и глубину L. Для организации дерева создадим структуру, соответствующую узлу дерева. Будем хранить в этой структуре количество монет x и вероятность p попадания в узел из узла предыдущего уровня. Учитывая метод решения, состоящий в последовательном пересчете рекуррентных соотношений из пункта 2.4.3, добавим в рассматриваемую структуру специальное поле для хранения текущего значения средней премии E. В результате получим следующие объявления:

const int b = 10;         // Степень дерева - B в постановке задачи
const int l = 7;          // Количество уровней дерева

const int MAX_VALUE = 20; // Максимальное значение в вершине дерева

int NodesCount;           // Количество узлов дерева = (1-b^l) / (1-b)
int BranchesCount;        // Количество ветвей дерева = NodesCount - 1;

typedef struct            // Узел дерева
{
  int value;              // Значение в узле
  // Вероятность попадания в узел из узла предыдущего уровня
  double probability; 
  // Компонент для подсчета среднего
  double expectation;  
} TreePart;

Учитывая регулярную структуру дерева, будем хранить его в виде массива узлов, располагая в нем узлы последовательно по уровням, от корня к листьям. Учитывая возможный большой размер массива, будем создавать его динамически в куче. В результате получим:

TreePart *RobotTree;  // Массив для хранения дерева.
// Схема хранения: 
// (V00) 
// (V10 V11 ... V1b) 
// (V21 V22... V2b^2)
// ...
// (Vl-1,1 Vl-1,2...Vl-1,b^(l-1)),
// где скобки стоят для наглядности. 
// Дерево упаковывается в одномерный массив по уровням.

Для удобства индексации и снижения накладных расходов предусмотрим однократное вычисление значения b в степени от 0 до l-1, а также номеров первых узлов каждого уровня дерева в массиве RobotTree.

// Вспомогательный массив для хранения значений b в степени 0...l-1
__int64 power[l];  
// Вспомогательный массив для хранения номера первого узла каждого уровня 
//  в массиве RobotTree
__int64 index[l];

Проектирование модульной структуры

Предусмотрим наличие в проекте файла robot.cpp, содержащего рассмотренные выше объявления, а также следующих функций:

// Ввод дерева
void InputTree(void);
// Освобождение памяти, выделенной для хранения дерева
void ReleaseTree(void);
// Функция вычисления максимума
__inline double max(double v1, double v2);
// Функция вычисления премии по значению в узле
__inline double func(double value);
// Вычисление средней премии - основная расчетная функция
double GetExpectation(void);
// Головная функция
int main(void);

Прокомментируем основные функции.

Функция InputTree предназначена для ввода исходных данных в соответствии с условием задачи. В этой функции вычисляется количество узлов и ветвей, выделяется память для хранения дерева, заполняются вспомогательные массивы power и index, инициализируется датчик случайных чисел и происходит заполнение дерева. При этом гарантируется выполнение условия 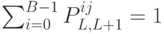. Рекомендуем на этапе отладки отключать инициализацию датчика, для того чтобы при каждом запуске работа велась с одним и тем же деревом, или инициализировать дерево заранее заготовленными данными, для которых вручную подсчитан правильный ответ.

Функция func предназначена для обобщения задачи на случай, когда размер премии при открывании двери является некоторой функцией от x. В рассматриваемой сейчас постановке она просто возвращает значение x.

Функция GetExpectation рассчитывает средний размер премии по дереву при помощи описанного выше метода. Приведем ее реализацию:

// Вычисление среднего
// Алгоритм базируется на следующих соотношениях:
// E_l,i = СУММА по j=0__b-1 (Probability_l+1,j * E_l+1,j + value_l,i),
// где l - уровень, i - номер узла в уровне, l+1,j - узлы потомки узла l,i.
// Учитывая, что на последнем уровне E_l-1,i = Value_l-1,i
// Вычиляем рекуррентное соотношения из конца в начало.
// В итоге имеем сумму для нулевого узла - корня дерева
double GetExpectation(void)
{
  // Последний уровень
  int i, j, level;
  double sum;
  TreePart rp;
  for (j = 0; j < power[l-1]; j++)
    RobotTree[j + index[l-1]].expectation = 
                                   func(RobotTree[j + index[l-1]].value);
  // Пересчет из конца в начало
  // Цикл по уровням
  for (level = l - 2; level >= 0; level--)
  {
    // Цикл по узлам уровня
    for (j = 0; j < power[level]; j++)
    {
      // Для узла level, j подсчитываем expectation
      // Цикл по потомкам
        sum  = func(RobotTree[ index[level] + j ].value);
        for (i = 0; i < b; i++)
        {
          rp = RobotTree[ index[level+1] + b * j + i ];
          sum = sum + rp.expectation * rp.probability;
        }
        RobotTree[ index[level] + j ].expectation = sum;
    }
  } 
  return RobotTree[0].expectation;
}