НОУ ИНТУИТ | Технологии построения и использования кластерных систем. Лекция 4: Отладка параллельной программы с использованием Intel Thread Checker

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 28.10.2009 | Доступ: свободный | Студентов: 516 / 40 | Оценка: 4.67 / 4.39 | Длительность: 20:33:00

Тема: Суперкомпьютерные технологии

Специальности: Программист, Системный архитектор, Архитектор программного обеспечения

|

Вам нравится? Нравится 11 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

11.2.2. Задача Дирихле

11.2.2.1. Постановка задачи

В качестве второго примера рассмотрим задачу из области численного решения дифференциальных уравнений в частных производных, а именно задачу Дирихле для уравнения Пуассона (см., например, [11.8]). Итак, необходимо найти функцию , удовлетворяющую в области определения уравнению

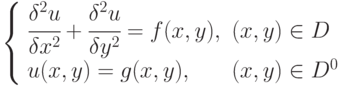
$\left \{ \begin{array} {ll}\cfrac{\delta^2u}{\delta x^2} + \cfrac{\delta^2u}{\delta y^2} = f(x,y), & (x,y) \in D \\ u(x,y) = g(x,y), & (x,y) \in D^0 \end{array}$

и принимающую на границе 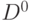D^0 области 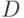значения g(x,y) .

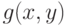11.2.2.2. Метод решения

Используя распространенный метод конечных разностей (он же метод сеток) перепишем уравнение Пуассона в конечно-разностной форме [11.9],

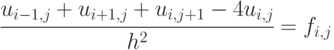
$\cfrac{u_{i-1,j}+ u_{i+1,j} +u_{i,j+1}-4 u_{i,j}}{h^2}=f_{i,j}$

Разрешив его относительно 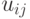$u_{ij}$ , получим

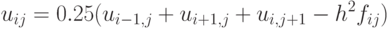
$u_{ij} = 0.25 (u_{i-1,j}+ u_{i+1,j} +u_{i,j+1}-h^2 f_{ij})$

Мы получили основу для построения итерационной схемы решения задачи Дирихле, в которой, отталкиваясь от некоторого начального приближения можно последовательно уточнять значения 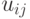$u_{ij}$ до достижения требуемой точности.

11.2.2.3. Последовательная реализация

Последовательная реализация данной итерационной схемы может выглядеть следующим образом:

do
{
  dmax = 0;
  for (i = 1; i < N - 1; i++)
  {
    for(j = 1; j < N - 1; j++)
    {
      temp = u[N * i + j];
      u[N * i + j] = 0.25 * (u[N * i + j + 1] + u[N * i + j - 1] + 
        u[N * (i + 1) + j] + u[N * (i - 1) + j]);
      dm = fabs(u[N * i + j] - temp);
      if (dmax < dm)
        dmax = dm;
    }    
  }
}
while (dmax > EPS);

Здесь dmax есть максимальная разность между "старым", с предыдущей итерации, и "новым", посчитанным на текущей, значениями и используется для принятия решения об окончании расчетов.

11.2.2.4. Параллельная реализация, вариант 1

"Сеточные" задачи, в которых решение получается выполнением набора из одних и тех же действий в каждом "узле" сетки обладают очень простой схемой распараллеливания. Достаточно сетку "порезать" на части: вертикально на столбцы, горизонтально на полосы, или и так и так, то есть на блоки, и распараллеливание выполнено. Если при этом объем вычислений, выполняемых в каждом узле, примерно одинаков, то и эффективность полученной параллельной реализации может быть довольно высока.

Таким образом, в данной работе мы рассмотрим две схемы распараллеливания решения задачи Дирихле. Первая - схема с максимальным параллелизмом, в которой сетка "режется" на блоки размера 1 на 1. Вторая - схема, в которой распределение вычислений осуществляется по строкам сетки.

В данной лабораторной работе нашей целью не является производительность получаемых параллельных реализаций, поэтому в качестве первого варианта, как было сказано выше, мы используем вариант с максимальным параллелизмом, который в OpenMP версии достигается распараллеливанием обоих циклов:

do
{
  dmax = 0;
  #pragma omp parallel for
  for (i = 1; i < N - 1; i++)
  {
    #pragma omp parallel for
    for(j = 1; j < N - 1; j++)
    {
      temp = u[N * i + j];
      u[N * i + j] = 0.25 * (u[N * i + j + 1] + u[N * i + j - 1] + 
        u[N * (i + 1) + j] + u[N * (i - 1) + j]);
      dm = fabs(u[N * i + j] - temp);
      if (dmax < dm)
        dmax = dm;
    }    
  }
}
while (dmax > EPS);

Конечно же, в представленном виде код является некорректным. В чем именно, нам предстоит выяснить, использую Intel Thread Checker.

11.2.2.5. Анализ реализации 1

Исследуем представленный выше код на наличие ошибок.

Для проверки правильности работы параллельной программы можно применить, казалось бы, естественный подход - сравнить результаты выполнения последовательной и параллельной версий. Например, в задаче умножения матриц результат должен быть один и тот же, независимо от применяемой вычислительной схемы. Вместе с тем, часто наблюдается и иная картина - именно так, как в рассматриваемом примере - результаты параллельной версии могут отличаться от результатов последовательной, но это не будет являться признаком наличия ошибок. Одна из причин различия результатов - изменения порядка выполнения операций вещественной арифметики, что может, в частности, привести к изменению величины получаемой погрешности вычислений. Ситуация усложняется, если вычислительная схема параллельного алгоритма отличается от исходного последовательного прототипа - так, в нашем примере, порядок обработки узлов вычислительной сетки в параллельной версии алгоритма может быть другим нежели в последовательном методе. Более того, результаты паралл ельных расчетов могут не совпадать при различных запусках даже при одних и тех же начальных данных, поскольку условия запуска (например, загрузка вычислительной системы) также могут влиять на порядок вычислений. Описанная проблема - различие выполняемых вычислений - является одной из принципиальных при разработке параллельных программ. Наличие такой проблемы приводит к тому, что при разработке параллельного метода необходимо тщательно анализировать идентичность вычислительных схем параллельных и последовательных расчетов, а при обнаружении различий доказывать корректность параллельной версии и определять способы проверки правильности выполнения параллельных расчетов (дополнительная информация по данному вопросу может быть получена, например, в материале "Отладка параллельной программы с использованием Intel Thread Checker" в [11.7]).

Рассматриваемый пример прекрасно демонстрирует описанные выше ситуации - вычислительная схема параллельного алгоритма отличается от последовательного метода (порядок обработки узлов вычислительной сетки может оказаться различным) и результаты параллельных вычислений могут отличаться от запуска к запуску. В теоретических работах показана корректность рассмотренной параллельный схемы вычислений - процесс вычислений сходится к решению поставленной задачи Дирихле. Данный математический результат дает подход для проверки правильности выполнения параллельной программы путем оценки точности получения требуемого результата вычислений (в силу сходимости параллельный алгоритм должен обеспечивать достижение любой наперед заданной точности расчетов). Иными словами, для проверки правильности можно сравнить результат параллельной программы с точным решением и, если результат совпадает с точным решением в пределах задаваемой точностью, то можно считать, что расчеты выполнены правильно. При этом, однако, следует понима ть, что такая проверка не дает полной гарантии - как и любое тестирование, правильность прохождения теста говорит о корректности работы программы только при данных исходных параметрах задачи (а в случае параллельных вычислений - о корректности только данного конкретного запуска программы). Необходимы многократные запуски при одних и тех же исходных данных, нужны различные варианты постановок решаемой задачи. Процесс тестирования становится трудоемким и длительным - все отмеченные моменты убедительно подтверждают необходимость использования инструментов отладки параллельных программ.

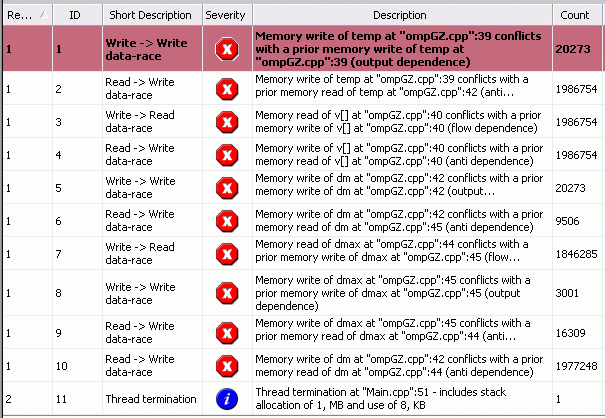
Проанализируем код с помощью Intel Thread Checker.

Рис. 11.11. Задача Дирихле - результат анализа параллельной реализации 1

Как видим, налицо существенное количество ошибок, которые ITC классифицирует как "гонка данных".

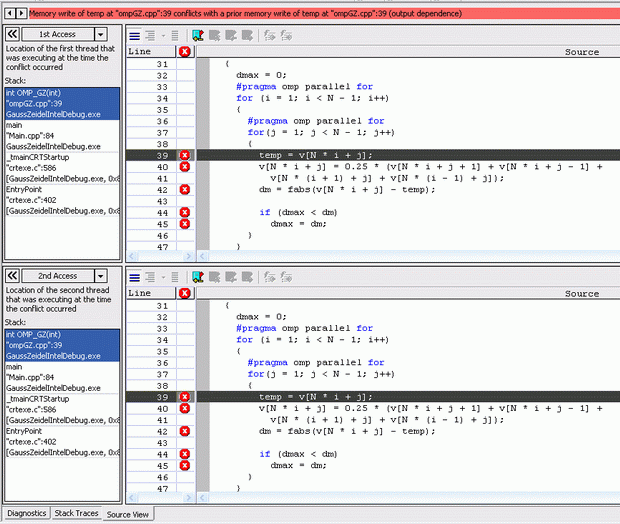
"Разворачивая" любую из них, мы получим информацию вида:

увеличить изображение
Рис. 11.12. Задача Дирихле - ошибка типа "гонка данных"

Как видим, диагностика ITC указывает нам и строку, в которой имеет место проблема, и переменную, с которой она связана. В выделенной строке обнаружен конфликт доступа к переменной temp, когда два потока могут пытаться одновременно записать в нее значения.

Решение выявленных проблем зависит от того, как используется та или иная переменная и может состоять в ее "локализации", то есть создании внутренней для каждого потока копии, как для переменной temp, или в синхронизации доступа к ней, если переменная нужна всем потокам, как в случае с dmax.

Заметим, что две из найденных ITC ошибок в данной реализации могут проявиться только при очень маленьком значении N. Какие именно, предлагаем читателям найти самостоятельно.

Корректируем код:

omp_lock_t dmax_lock;

omp_init_lock(&dmax_lock);
do
{
  dmax = 0;
  #pragma omp parallel for
  for (i = 1; i < N - 1; i++)
  {
    #pragma omp parallel for private(temp, dm)
    for(j = 1; j < N - 1; j++)
    {
      temp = v[N * i + j];
      v[N * i + j] = 0.25 * (v[N * i + j + 1] + v[N * i + j - 1] + 
        v[N * (i + 1) + j] + v[N * (i - 1) + j]);
      dm = fabs(v[N * i + j] - temp);
      
      omp_set_lock(&dmax_lock);
      if (dmax < dm) 
        dmax = dm;
      omp_unset_lock(&dmax_lock);
    }    
  }
}
while (dmax > EPS);

omp_destroy_lock(&dmax_lock);

По результатам запуска убеждаемся, что параллельная версия работает корректно. Снова запускаем Thread Checker и видим.

Рис. 11.13. Задача Дирихле - результат анализа параллельной реализации 1 после исправления

Прав или нет ITC в своих подозрениях относительно последнего варианта кода предлагаем читателям выяснить самостоятельно.

11.2.2.6. Параллельная реализация, вариант 2

Второй вариант распараллеливания, который мы будем использовать в данной работе, состоит в уменьшении степени параллелизма реализации, что, тем не менее, ведет к увеличению эффективности. Вариант заключается в распараллеливании только внешнего цикла и дополнительно предполагает некоторые изменения в схеме подсчета значения dmax:

do
{
  dmax = 0;
  #pragma omp parallel for
  for (i = 1; i < N - 1; i++)
  {
    dm = 0;
    for(j = 1; j < N - 1; j++)
    {
      temp = u[N * i + j];
      u[N * i + j] = 0.25 * (u[N * i + j + 1] + u[N * i + j - 1] + 
        u[N * (i + 1) + j] + u[N * (i - 1) + j]);
      d = fabs(u[N * i + j] - temp);
      if (dm < d)
        dm = d;
    }    
    if (dmax < dm) 
      dmax = dm;
  }
}
while (dmax > EPS);

Как и в первом случае представленный код содержит ошибки, которые необходимо найти с помощью Intel Thread Checker и устранить.

11.2.2.7. Анализ реализации 2

Прежде всего, отметим, что в связи с изменившейся схемой работы и рассмотренная выше параллельная версия и данная могут не давать идентичные результаты по сравнению с последовательным кодом, что, конечно, является дополнительным усложняющим моментом для "ручной" отладки.

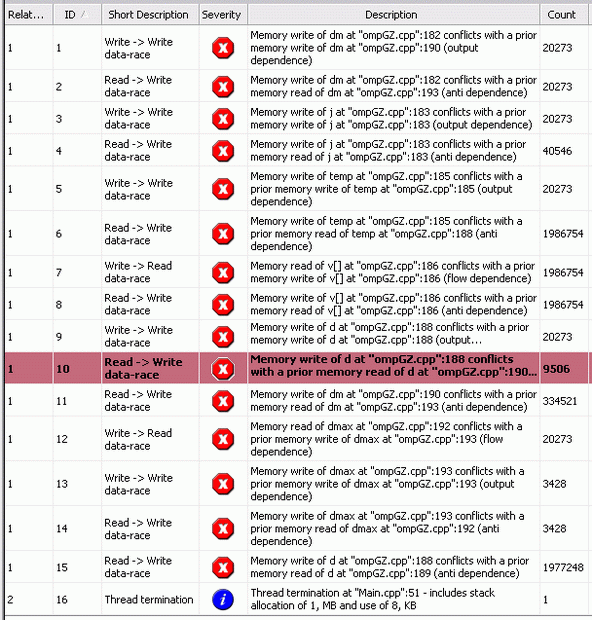
Проанализируем код с помощью Intel Thread Checker.

увеличить изображение
Рис. 11.14. Задача Дирихле - результат анализа параллельной реализации 2

Количество ошибок в этой версии еще больше в связи с увеличившимся количеством переменных, кроме того, в список попала переменная j, заботу о которой раньше "брал не себя" компилятор - как известно переменную цикла в директиве #pragma omp parallel for не обязательно объявлять как private.

Также как и для варианта 1 исправление найденных ошибок заключается в локализации необходимых переменных и использовании синхронизации при работе с переменной dmax.

omp_lock_t dmax_lock;

omp_init_lock(&dmax_lock);
do
{
  dmax = 0;
  #pragma omp parallel for private(j, temp, d, dm)
  for (i = 1; i < N - 1; i++)
  {
    dm = 0;
    for(j = 1; j < N - 1; j++)
    {
      temp = v[N * i + j];
      v[N * i + j] = 0.25 * (v[N * i + j + 1] + v[N * i + j - 1] + 
        v[N * (i + 1) + j] + v[N * (i - 1) + j]);
      d = fabs(u[N * i + j] - temp);
      if (dm < d)
        dm = d;
    }        
    omp_set_lock(&dmax_lock);
    if (dmax < dm) 
      dmax = dm;
    omp_unset_lock(&dmax_lock);
  }
}
while (dmax > EPS);

omp_destroy_lock(&dmax_lock);

Снова запускаем ITC.

Рис. 11.15. Задача Дирихле - результат анализа параллельной реализации 2 после исправления

Как и выше ITC нашел проблему там, где ее на самом деле нет. Почему это так, предлагаем читателям выяснить самостоятельно. В качестве подсказки: вспомните характер распределения итераций цикла for при использовании директивы #pragma omp parallel for без дополнительных параметров.

Дальше >>

Авторизоваться

Технологии построения и использования кластерных систем

Отладка параллельной программы с использованием Intel Thread Checker