НОУ ИНТУИТ | Нейросетевые технологии искусственного интеллекта. Лекция 13: Обучаемые и самообучающиеся системы распознавания, управления и принятия решений на логических нейронных сетях

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 29.10.2019 | Доступ: свободный | Студентов: 835 / 111 | Длительность: 17:21:00

Тема: Искусственный интеллект и робототехника

|

Вам нравится? Нравится 14 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Аннотация: Рассматривается применение логических нейронных сетей в ассоциативных "бесформульных" вычислениях трудно формализуемых задач и задач имитационного моделирования, в медицинских информационно-справочных системах, в системах идентификации пользователя, в адаптивной пошаговой маршрутизации беспроводных телекоммуникационных и транспортных сетей, а также в самообучающихся системах управления по нечётким данным. Приводятся рекомендации по повышению качества некоторых известных систем принятия решений.

Щ о е в... (Углублённо.) Пускай теперь наука трудится,

а человек около неё как на курорте.

А. Платонов. "Шарманка".

Аппроксимация опыта и ассоциативные "бесформульные" вычисления

Давно известно, что исследователи, использующие современный метод имитационного моделирования сложных систем, прекратили попытки построения функций аппроксимации для графического представления своих результатов. Большое количество формально несовместимых факторов приводило бы к формированию большого количества двух- и трёхмерных таблиц для выделенных переменных. Эти таблицы составлялись бы для фиксированных значений других переменных, рассматриваемых в качестве параметров, составляющих множество точек в многомерном пространстве. Наглядность такого представления при желании получить огромное количество графиков, проблематична.

Исследователи формируют базы знаний, представляя свои результаты в виде таблиц, связывающих испытываемые точки факторного пространства (ситуации) с векторами найденных значений результатов – решений по данным ситуациям. Наиболее характерно это для полигонных испытаний, используемых для калибровки моделей. Таким образом, для дальнейших исследований предоставляется далеко не полная оценка результатов моделирования во всём факторном пространстве.

Чтобы превратить эти оценки в количественные на всём факторном пространстве при допущении об отсутствии особых точек, необходимо создать механизм расширения их на всю испытываемую область. Используется метод ассоциативного нахождения "промежуточных" решений, заключающийся в определении: "на какую (какие) из известных ситуаций и в какой мере похожа вновь возникшая ситуация и как по базе знаний выбрать или построить соответствующее ей решение". При этом по нескольким "похожим" ситуациям возможно усреднённое решение.

Механизмом, представляющим собой численный метод "бесформульного" ассоциативного вывода, и являются логические нейронные сети. С их помощью реализуются развиваемые информационно-справочные системы, объединяющие опыт и результаты моделирования в конкретной области исследований.

Например, в [7] исследуются результаты моделирования многосерверной базы данных с циркулирующими сегментами. Для множества точек факторного пространства – значений векторов ${\lambda (интенсивность потока запросов), \tau (длительность такта), t_{вып} ("чистое" время выполнения запроса), n (количество серверов), m (количество циркулирующих сегментов)}$ , находятся значения вектора {среднее время выполнения запроса, вероятность выполнения}.

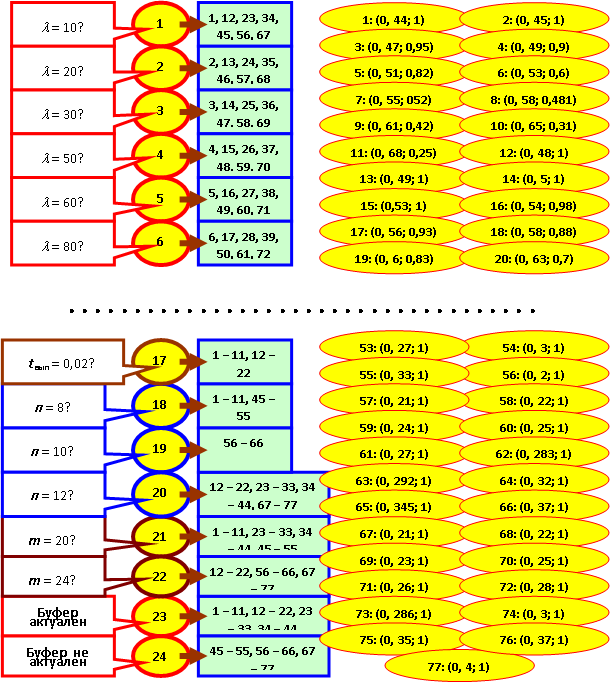
Информационной основой построения обученной нейронной сети (рис. 13.1) для информационно-справочной системы являются таблицы, построенные в процессе моделирования.

Значение V_i простейшей функции активации i-го нейрона находится в результате расчётов:

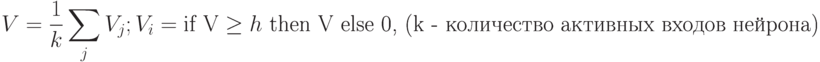$V=\frac{1}{k}\sum_{j}V_j; V_i=\text{if V}\geq h \text{ then V else 0, (k - количество активных входов нейрона)}$

( 13.1)

Здесь V_j – величина возбуждения рецептора, подаваемая на вход нейрона. В нашем случае k = 6.

Максимально возбудившийся нейрон указывает на решение. Решением является вектор, состоящий из двух компонент – времени t_вып выполнения запроса и вероятности Р его выполнения.

Направление синапсических связей на рисунке указано во вставках, а решения обозначены на "телах" нейронов парой искомых чисел.

Поскольку исследования многопроцессорных баз данных далеки от завершения, веса всех синапсических связей на рис. 13.1 приняты равными единице. Пока мы не можем с достаточной уверенностью установить, в какой степени каждый фактор влияет на получаемый результат. Это может быть выявлено в течение длительного опыта эксплуатации.

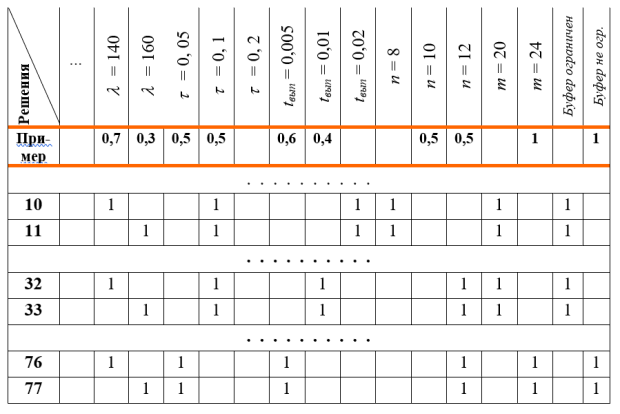
Обработка нейросети основана на её представлении в виде матрицы связей, фрагмент которой показан в табл. 13.1. Она легко обрабатывается с помощью EXEL.

Например, пусть известны значения факторов создающейся многосерверной базы данных с циркулирующими сегментами: 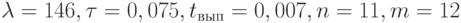$\lambda = 146, \tau = 0,075, t_{вып} = 0,007, n = 11, m = 12$ , размер буфера не актуален из-за значительного объёма памяти сервера.

Рис. 13.1. Фрагмент информационно-справочной системы

Для возбуждения рецепторов (в строке "Пример") разделим для каждого фактора "единицу" обратно пропорционально расстоянию до двух "близких" рецепторов: V₁₀ = 0,7, V₁₁ = 0,3, V₁₂ = V₁₃ = 0,5, V₁₅ = 0,6, V₁₆ = 0,4, V₁₉ = V₂₀ = 0,5, V₂₂ = 1, V₂₄ = 1.

увеличить изображение
Фрагмент матрицы связей для логической нейронной сети, реализующей информационно-справочную систему

Считаем функцию активации всех нейронов 1 – 77 скалярным умножением каждой его строки в матрице на строку "Пример". Полученные результаты делим на 6, так как каждый нейрон имеет 6 входных связей, и сравниваем с порогом h.

В общем случае порог выбирается экспериментально, чтобы отсечь малые значения возбуждения нейронов. В данном случае представляется целесообразным принять h = 0,6. Чтобы не загромождать пример, в табл. 13.1 отражены строки матрицы следования, соответствующие лишь некоторым нейронам, с ожидаемым существенным возбуждением.

Полученные значения возбуждения нейронов:

V₁₀ = V₁₁ = V₃₂ = V₃₃ = 0, V₇₆ = 0,71, V₇₇ = 0,65. По другим строкам матрицы следования возбуждения равны нулю.

Находим 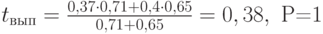$t_\text{вып}=\frac{0,37\cdot 0,71 + 0,4\cdot 0,65}{0,71+0,65}=0,38, \text{ P=1}$

Медицинские информационно-справочные системы

Если ассоциативные "бесформульные" вычисления допускают усреднение решения, то в медицинских системах диагностики и лечения результат должен быть вполне определённым, как руководство к действию. В большинстве случаев речь идёт о получении чёткого решения по нечётким данным. Это подтверждается практикой привлечения консилиума при решении спорных вопросов. Поэтому построение базы знаний на основе опыта высококвалифицированных специалистов и её организация на базе механизма ассоциативного мышления, реализуемого логической нейронной сетью, является чрезвычайно важной задачей.

Исключение операции усреднения при использовании логической нейронной сети говорит о том, что единственный максимально возбудившийся нейрон выходного слоя указывает на предлагаемое решение. Более того, это решение редко является численным – в этом случае усреднение было бы допустимо. В основном, решение указывает на стратегию или алгоритм лечения.

В [15] представлена логическая нейронная сеть, реализующая информационно-справочную систему для лечения хронических заболеваний почек. В основе этой системы лежат клинические практические рекомендации Международной Рабочей группы специалистов. Объём статьи не позволил в рамках одного рисунка поместить сформированную логическую нейронную сеть. Она отражена полностью, но фрагментарно. Матрица связей (табл. 13.2), как аппарат вычислений, там не отражена.

Табл. 13.2. Матрица связей, левая и правая части (Правую часть следует рассматривать в совокупности со столбцом обозначений решений в левой части)

увеличить изображение
Табл. 13.2. Матрица связей, левая и правая части (Правую часть следует рассматривать в совокупности со столбцом обозначений решений в левой части)

увеличить изображение

Рассмотрим пример запроса. Пусть из-за неточного измерения скорости клубковой фильтрации (СКФ) с достоверностью 0,6 (по приблизительной оценке врача) установлено, что наблюдается 5-я стадия ХЗП – хронического заболевания почек. Предполагаемая достоверность 4-й стадии составляет 0,4. Возбуждается рецептор 6 сообщением ему значения 0,6. Рецептору 15 сообщается значение 0,4. Далее, пусть из-за неточного замера уровня фосфора в сыворотке крови рецептору 18 пришлось задать значение возбуждения 0,8, а рецептору 19 - значение 0,2. Аналогично, с учётом ошибок измерения интактного ПТГ (паратгармона) формируются значения 0,2, 0,2, 0,6 возбуждения рецепторов 20, 21 и 22 соответственно. Запрос сформирован, возбуждение остальных рецепторов полагаем нулевым. При нулевом значении порога максимально, до величины 1,4, возбудится нейрон, соответствующий решению Y₂₂ = <Поддерживать содержание фосфора сыворотки крови на уровне 2,7 мг/дл и выше, но не выше чем 4,6 мг/дл. Следует обеспечить терапию активными стеролами витамина D и т.д. >

Идентификация пользователя в компьютерной сети по "почерку"

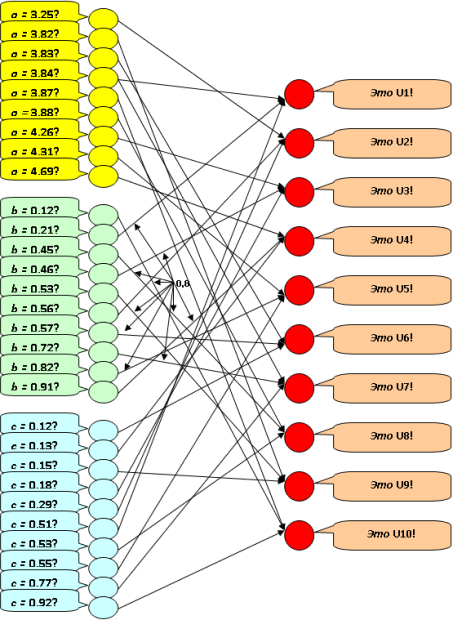
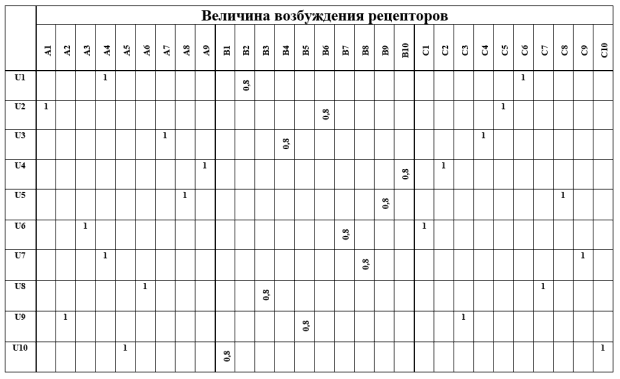
Для примера выберем три характеристики почерка пользователя в системе "клиент – сервер", образующие его "портрет": скорость использования клавиш a(key/s), частоту использовании стрелки 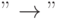$"\to"$ возврата b(key/s), частоту использования клавиши "delete" c(key/s).

В [16] на основе статистического анализа десяти пользователей получены оценки данных характеристик (табл. 13.3). Не подвергая их сомнению, рассматривая лишь в качестве примера, используем эти оценки, отображающие накопленный опыт, для построения логической нейронной сети. При этом предположим, что в результате длительных испытаний и эксплуатации, установлено неодинаковое влияние выделенных характеристик пользователя на результат распознавания.

Таблица 13.3. "Портреты" пользователей
Пользователь	Скорость ввода символов a(key/sec)	Частота использования клавиши 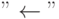$"\leftarrow"$ b(key/sec)	Частота использования клавиши delete c(key/sec)
U1	3,84	0,21	0,51
U2	3,25	0,56	0,29
U3	4,26	0,46	0,18
U4	4,69	0,91	0,13
U5	4,31	0,82	0,55
U6	3,83	0,57	0,12
U7	3,84	0,72	0,77
U8	3,88	0,45	0,53
U9	3,82	0,53	0,15
U10	3,87	0,12	0,92

А именно, пусть в результате оценок оказалось целесообразным учитывать характеристику b с весом 0,8 (рис. 13.2).

Выберем функцию f_i активации i-го нейрона, предварительно рассчитав значение 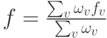$f=\frac{\sum_{v}\omega_v f_v }{\sum_{v}\omega_v}$ Тогда f_i = f, если 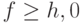$f \geq h, 0$ – в противном случае. (13.2)

Здесь 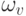$\omega_v$ - вес входной связи, параметр v "пробегает" по всем входным связям нейрона.

увеличить изображение
Рис. 13.2. Логическая нейронная сеть для распознавания пользователя в системе "клиент – сервер"

Обозначим высказывания: А1 = <a = 3,25? >, ... C10 = <c = 0,92? >. Матрица связей представлена в табл. 13.3.

увеличить изображение
Табл. 13.3. Матрица связей логической нейронной сети распознавания пользователя

Рассмотрим пример. Пусть сервер, периодически контролируя работающих пользователей, рассчитал вектор статистических характеристик {a = 3,4, b = 0,51, c = 0,3}. Порог распознавания h = 0,6.

Находятся два рецептора группы a, "близких" к значению 3,4, и "единица" делится между ними обратно пропорционально "расстоянию". В данном случае возбуждение А1 принимается равным 0,75, а А2 – 0,25. Аналогично находятся два рецептора, включающих значение b = 0,54, – В5 и В6. Тогда возбуждение первого полагается равным 0,67, а второго – 0,33. Аналогично, рецептор С5 возбуждается на величину 0,9, а рецептор С6 на величину 0,1.

С помощью функции активации найдём величины возбуждения нейронов выходного слоя. Максимальная из этих величин - величина возбуждения нейрона, указывающего на пользователя U2 и превысившая порог, равна 0,61.

Адаптивная пошаговая маршрутизация в беспроводной телекоммуникационной сети

Рассмотрим беспроводную телекоммуникационную систему, в которой компьютеры узлов составляют вычислительную сеть [17]. На этой сети задано отношение смежности. Информационные пакеты движутся к адресату по смежным компьютерам (узлам). Каждый маршрут не формируется весь сразу, а реализуется динамически, по шагам с учётом приоритетного обращения к смежным узлам (в зависимости от адреса назначения), текущей загрузки этих узлов и текущей оценки качества связи между узлами (в [17] не учитывается). Лишь в результате такого комплексного анализа может быть окончательно выбран узел смещения. Таким образом, одновременно реализуемые маршруты в сети оказывают взаимное влияние, и "разводить" их динамически надо так, чтобы избегать пиковых нагрузок узлов и, в конечном итоге, обеспечить максимальную пропускную способность сети, а также максимальную вероятность выполнения передачи.

На каждом i-м узле есть таблица T_i (табл. 12.4) предпочтительного смещения при передаче данных на все прочие узлы, кроме смежных.

Таблица 13.4. Таблица предпочтительного смещения из данного i-го узла для каждого (не смежного) адреса назначения
Узел (адрес) назначения	Вес смежного узла в направлении передачи
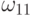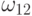А₁	$\omega_{11}$	$\omega_{12}$	.....	$\omega_{1K}$
........	...	...	.....	...
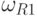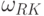А_R	$\omega_{R1}$	$\omega_{R2}$	.....	$\omega_{RK}$

Здесь R – количество узлов, в которые возможна передача пакетов из данного узла через один из смежных, K – количество смежных узлов. (В общем случае К – переменная величина.)

При выборе весов 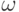$\omega$ учитывается территориальное взаимное расположение узлов. Так, очевидно, что приоритетной является та передача, при которой пакет приближается к узлу назначения, хотя в динамике загрузки сети может оказаться, что "кружной" путь ближе "прямого".

Предполагается, что компьютер каждого узла имеет буфер, в котором накапливаются пакеты для дальнейшей отправки. Перегрузка буферов (точнее, - достижение критической отметки) должна блокировать приём новых пакетов. Возможна блокировка передач по направлениям или в сети в целом. Потери информации не предполагаются, пользователь должен быть информирован об этой перегрузке для повторения запроса позже.

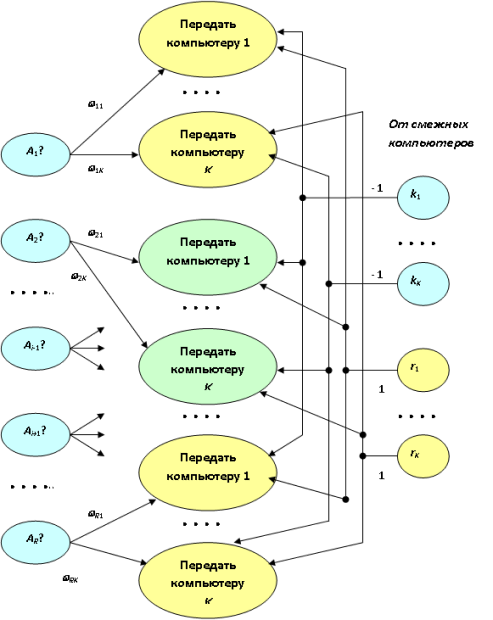
Управление передачей пакетов производится с помощью логической нейронной сети, которая первоначально использует для каждого адреса предпочтительные направления передачи пакетов смежным узлам, найденные в табл. 13.4. Веса этих смещений используются в качестве весов синапсических связей. С помощью обратных связей, осуществляемых смежными узлами, с отрицательными весами передаются коэффициенты k_j загрузки этих узлов, а также (с положительными весами) оценки $r_j \leq 1 (j = 1,..., K)$ состояния связи между данным и смежным узлами, которые окончательно влияют на выбор смежного узла для передачи пакета. (Значение k_j следует интерпретировать, как достоверность высказывания о том, что буфер узла загружен полностью, а значение r_j – как достоверность высказывания о том, что качество связи между передающим и j-м узлами отличное.) Нейронная сеть фрагментарно распределена между компьютерами всех узлов так, чтобы отражать информацию, связанную только с конкретным узлом.

Фрагмент логической нейронной сети, размещённый на одном узле, представлен на рис. 13.3. Здесь 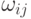$\omega_{ij}$ – предпочтительные веса смежных узлов при передаче пакета по адресу A_i, k_j – коэффициент загрузки буфера смежного узла, r_j – состояние связи между узлами.

увеличить изображение
Рис. 13.3. Фрагмент логической нейронной сети, размещённый на одном узле, во взаимодействии со смежными узлами

Функция активации, по аналогии с (13.1) и (13.2) имеет вид:

$V_j = V_{Ai} \omega_{ij} – k_j + r_j$ , если эта разность превышает порог h,

0, в противном случае.

Здесь V_Ai = 1, если А_i (i = 1, ..., R) – адрес назначения информационного пакета, порог h выбирается экспериментально так, чтобы предпочтение могло быть выбрано между не полностью загруженными узлами.

Таким образом, в результате обратной связи максимального возбуждения может достичь совсем не тот смежный узел, которому первоначально было оказано предпочтение.

Общим критерием эффективности управления является максимизация пропускной способности сети. Частными критериями являются: 1) минимум среднего времени выполнения запроса на передачу пакета в сети; 2) минимум времени ожидания пользователем возможности выполнения своих запросов.

Рассмотренный подход легко распространяется на выбор оптимального множества маршрутов совместного следования объектов в транспортной сети.

Некоторые "незаконченные" системы принятия решений

Контроль космического пространства

Особую важность применение представленного метода ассоциативных вычислений обретает в системе контроля космического пространства. При трудностях политического характера непрерывное наблюдение всех космических объектов, особенно спутников, затруднительно. Как правило, спутник скрывается за горизонтом от средств обнаружения и сопровождения, а затем появляется вновь. Средства обнаружения производят селекцию и идентификацию на основе текущего состояния каталога, представляющего собой базу знаний о космическом пространстве. Новый объект должен быть внесён в каталог с измеренными параметрами.

Каталог строится в виде логической нейронной сети. Для каждого спутника за отдельными рецепторами закрепляются значения шести известных параметров орбит. (Если уже существует рецептор, закреплённый за необходимым значением, он используется повторно.) Связи от этих рецепторов с единичными весами идут на нейрон, "отвечающий" за спутник, обладающий этими значениями параметров.

Тогда, для вновь возникших из-за горизонта объектов, методом ассоциативных вычислений с заданной точностью устанавливается совпадение с одним из известных спутников. Если спутник уже отображён в каталоге, то есть, возбуждение некоторого нейрона максимально превысило порог, продолжается его сопровождение. Если спутник новый, нейронная сеть дополняется на основе его характеристик, измеренных средствами обнаружения. Таким образом, логическая нейронная сеть, отображающая каталог, постоянно развивается.

Нейросетевое управление перехватом "быстрой" цели

Материал данного раздела не лишён элементов фантастики, в очевидном понимании того, что все крупные проекты рождаются на основе здоровых фантазий их исполнителей, первоначально исходящих из простейших предположений.

Под "быстрыми" целями будем понимать крупные метеориты и другие космические или баллистические (с ограниченным манёвром) объекты.

Следовательно, перехватчик должен быть столь же "быстрым". Это переносит тяжесть оперативного управления его действиями на этап предстартовой подготовки для движения в точку вывода и захвата цели видео средствами, а затем - на этап наведения на цель с помощью изменения силы и направления суммарной тяги двигателей.

Сценарий перехвата

Представим подробнее типовой сценарий перехвата.

Средства обнаружения целей в соответствии с тактовой частотой работы системы передают координаты предполагаемых целей и координаты векторов скорости на вычислительные средства командного пункта (КП). Передача сообщений по каждой цели на КП начинается с момента выполнения критерия обнаружения.
КП производит целераспределение, выбирая для каждой цели ближайший стрельбовый комплекс и конкретную стартовую позицию с предпочтительной возможностью встречного сближения с целью. Очевидно, что в динамике боя предпочтения могут не выполняться. Отнесём многочисленные "если" к последующему расширению условий решения задачи.
Перехватчику, назначенному для поражения конкретной цели, назначаются время старта, начальные установки его рулевых органов для движения в область точки вывода после вертикального старта, а также команды на устройство стабилизации для принятия положения в пространстве в соответствии с понятиями "верх" и "низ", упрощающими управление на этапе наведения. Мы предполагаем, что даже при позиции перехватчика для вертикального старта механический разворот в сторону цели недопустим, так как требует много времени. Поэтому для перехватчика, находящегося на стартовой позиции, "верх" и "низ" могут резко не соответствовать направлению на цель. Ведь перехватчик даже может оказаться "вверх ногами" к началу этапа наведения.
При боковой стрельбе по пролетающей цели точка вывода может явиться той упреждающей точкой, в которой осуществляется самоподрыв перехватчика.
При "пролёте" цели точка вывода соответствует исходному положению для погони.
При встречном перехвате или при погоне этап вывода заканчивается визуализацией цели, поступлением сигнала перехватчика "цель вижу". Если перехватчик с помощью своих средств цель "не увидел", команда на подрыв (главная команда) может быть подана с земли. Если перехватчик оборудован средствами виртуальной реальности, он может быть переведён на ручное управление с земли, если позволяют параметры движения.

Рис. 13.4. Перехватчик
В режиме встречного наведения или погони перехватчик видит цель на мониторе или его невидимом аналоге, например, в области памяти. С помощью органов управления он стремится совместить точку или образ цели с центром монитора. При максимальном сближении производится самоподрыв, несмотря на возможность столкновения.

Модель перехватчика

Предположим, что перехватчик имеет маршевый двигатель для основной тяги и четыре двигателя переменной тяги для смены направления движения созданием крутящего момента вокруг центра масс (рис. 13.4). С помощью маршевого двигателя производится и форсаж.

Перехватчик может иметь один двигатель с размноженными соплами. Четыре из них с помощью условной "ручки" осуществляют переменную тягу для управления движением. Режим форсажа влияет на все сопла.

Таким образом, управление направлением движения производится и условно отображается "ручкой", словно управляющей автоматом-перекосом вертолёта. Боковая составляющая движения ручкой означает поворот, продольная составляющая – изменение высоты.

Уточним, что перехватчику, назначенному для поражения цели, сообщается начальное положение "ручки", чтобы после вертикального старта обеспечить начальные углы движения к точке вывода по оптимальной траектории. Кроме того, могут сообщаться команды на стабилизаторы для придания в полёте вертикального положения. Однако такое положение навстречу цели может быть ему придано (вместе с группой других перехватчиков) заранее, на этапе предстартовой подготовки в соответствии с направлением обнаруженного налёта.

Как ранее указывалось, для обучения управляющих нейронных сетей и имитации хода боевых действий (использование натурных экспериментов желательно, но весьма дорого) необходима достаточно точная математическая модель интегрирования движения перехватчика, учитывающая не только силу тяги и гравитацию, но и рулевые эффекты. Вряд ли необходимая "математика" сейчас разработана.

Рекомендуем проводить интегрирование движения перехватчика, как неуправляемого снаряда в реальном или псевдореальном (в режиме обучения нейросети) времени приближёнными численными методами. Затем в каждом такте в найденные координаты следует вводить поправки на основе эмпирических данных, складывающихся на основе ограниченного опыта "учителя". Эти поправки, найденные экспериментальным путём или на основе опыта и знаний "учителя", таят в себе зависимости от текущего положения объекта по отношению к цели, их векторов скорости, угловой скорости вращения на основе уже установленных рычагов управления, поправок, введённых в предыдущие такты управления и т.д.

Представим более подробную "математику", вполне применимую для исследований принципов управления.

Пусть $\Delta$ – длительность такта управления перехватом, определяющая шаг интегрирования, i = 0, 1, ..., – номер такта. Тогда интегрирование в системе декартовых координат Oxyz, связанной со стартовой позицией, можно вести по формулам:

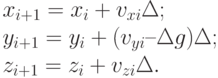
$x_{i+1} = x_i + v_{xi} \Delta;\\ y_{i+1} = y_i + (v_{yi} – \Delta g)\Delta;\\ z_{i+1} = z_i + v_{zi} \Delta.$

Здесь v_xi, v_yi, v_zi – координаты вектора скорости, g – ускорение свободного падения.

Как говорилось выше, при вертикальном старте значение v₀ устанавливается начальным положением "ручки" с командного пункта. Предположим, что значения координат вектора скорости v_x0, v_y0, v_z0 достигаются через несколько тактов неуправляемого полёта перехватчика после старта. Следовательно, отсчёт тактов управляемого движения (i = 0) начинается с этого момента времени.

Результаты интегрирования должны быть скорректированы в соответствии с текущим положением "ручки". Здесь-то и срабатывает логическая нейронная сеть, которая по ряду предыдущих и по текущему положению "ручки" находит поправки 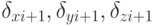$\delta_{xi+1}, \delta_{yi+1}, \delta_{zi+1}$ к полученным значениям координат перехватчика:

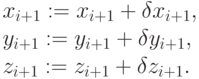
$x_{i+1} := x_{i+1} + \delta x_{i+1},\\ y_{i+1} := y_{i+1} + \delta y_{i+1},\\ z_{i+1} := z_{i+1} + \delta z_{i+1}.$

Находятся новые составляющие вектора скорости:

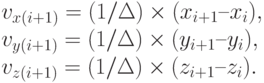
$v_{x(i+1)} = (1/\Delta ) \times (x_{i+1} – x_i),\\ v_{y(i+1)} = (1/\Delta ) \times (y_{i+1} – y_i),\\ v_{z(i+1)} = (1/\Delta ) \times (z_{i+1} – z_i).$

Уточнённые таким образом параметры движения влияют на последующие результаты интегрирования, изменяя траекторию движения перехватчика.

Несомненно, необходимые значения поправок 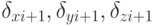$\delta_{xi+1}, \delta_{yi+1}, \delta_{zi+1}$ могут быть найдены строго математически на основе физических законов движения, динамически учитывающих управляющие воздействия. Однако научный опыт учит, что всякое "точное" громоздкое математическое описание использует предположения, условия и ограничения. Поэтому элементы строгих математических описаний, эвристические решения и обобщённые результаты эксперимента следует разумно сочетать для сокращения объёма вычислений.

Ведь концепции искусственного интеллекта как раз и строятся на нечётких данных! Что бы было, если бы обучение водителя авто строилось на основе строгого математического обоснования его действий?

Управляющие логические нейронные сети

Таким образом, применяются три системы принятия решений на логических нейронных сетях:

Система целераспределения на командном пункте, выдающая координаты и вектор скорости в точке вывода, контрольное время полёта, а также положения "ручки" для начального движения назначенного перехватчика в направлении точки вывода.
Бортовая система управления полётом, выбирающая положение "ручки" для устранения рассогласования движения перехватчика с уточняемой точкой вывода.
Система управления "ручкой" при визуальном наведении перехватчика на цель.

Управление надёжностью

Проблема управления надёжностью представляет яркий пример трудно формализуемой задачи, когда известны лишь частные математические зависимости для отдельных объектов и процессов, и то – с серьёзными допущениями. Комплексная автоматизация выполнения планов замещения оборудования, назначения сроков регламентных работ, и других средств поддержания надёжности сложной системы на требуемом уровне достигается в результате математического моделирования и обработки значительного опыта эксплуатации. В результате таких работ может быть создана база знаний на основе логической нейронной сети. Эта БЗ должна вестись опытными исследователями и постоянно уточняться.

В применении к железнодорожному транспорту, в условиях ограниченного финансирования, решение такой задачи влияет на порядок ремонта и модернизации объектов. Используется большое число контролируемых факторов: от прогнозируемой частоты отказов каждого транспортного средства до комплектации пожарных щитов, от срока эксплуатации железнодорожного перегона до наличия и обеспечения безопасности транспортного переезда и пассажирского перехода. Объединение показателей этих факторов в рамках единого метода ассоциативных вычислений возможно только при сведении их к единой системе измерения - к использованию достоверности высказываний о принадлежности данных: о наличии тех или иных объектов, о предполагаемых или прогнозируемых диапазонах надёжности транспортных средств и т.д. Скорее всего, данная трудно формализуемая задача относится к задачам нахождения рейтинга каждого объекта в общей очереди всех объектов на обслуживание. Рекомендуемые решения опираются не на строгие численные оценки, которые могли бы быть результатом расчёта функций численных переменных. Они указывают на предпочтительные стратегии развития и модернизации, на предпочтительный ряд возможных действий, распределение объёма финансирования ремонта объектов и т.д.

Решение формируется в виде текстов, подобных тем, что выдаются медицинской информационно-справочной системой.

Данную СПР можно существенно развить, продлив её логическую цепочку, введя второй логический уровень. На первом логическом уровне следует ограничиться нахождением текущего значения рисков, связанных с дальнейшей эксплуатацией объектов. Полученные данные совместно с другими данными, например, отображающими возможности финансирования, а также технологические и организационные возможности, следует использовать в следующей, однослойной логической нейронной сети – сети второго логического уровня. Эта сеть выдаёт окончательные конкретные рекомендации по тактике адресного проведения регламентных или ремонтных работ, по развитию инфраструктуры на основе новых требований, замене средств подвижного состава, прокладке путей и т.д. Примерный вид такой двухуровневой сети показан на рис. 13.5.

Реализация такой, всего лишь двухуровневой логической цепочки (длины, равной двум) должна послужить высокому уровню автоматизации и интеллектуализации системы управления, значительному подавлению человеческого фактора, повышению эффективности этой системы.

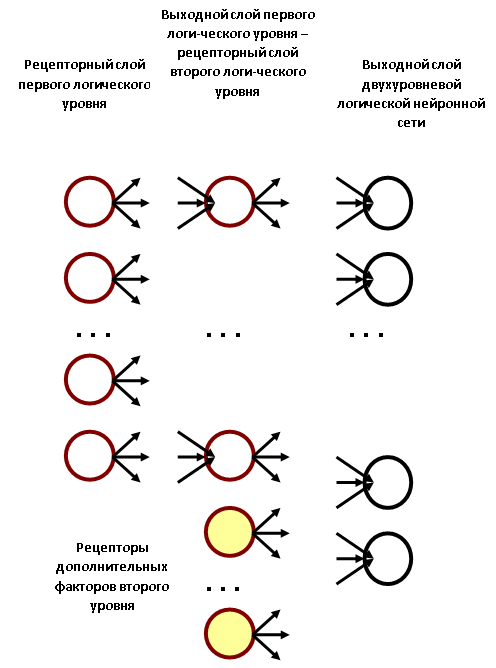
Рис. 13.5. Примерный вид логической нейронной сети, реализующей логическую цепочку с длиной, равной двум

Применение матриц связей позволяет оперативно изменять и дополнять СПР новыми или уточнёнными связями и их весами на основе опыта эксплуатации. Так осуществляется обратная связь, позволяющая на основе эффективности принимаемых решений корректировать эти решения, то есть, неограниченно развивать базу знаний.

Самообучающиеся системы управления

Рассмотрим, по-видимому, единственный человеческий опыт построения самообучающейся системы управления на основе Правил стрельбы наземной артиллерии времён Великой Отечественной Войны (рис. 13.6).

Для расчёта начальных установок при стрельбе батареей с закрытой огневой позиции стреляющий пользовался Таблицами стрельбы, составленными для каждого типа орудий при полигонных испытаниях. Такая таблица может служить прообразом базы знаний, реализуемой логической нейронной сетью.

Рис. 13.6. Объект самообучения

Затем по цели или реперу следовала пристрелка одним орудием, при которой объект захватывался в широкую вилку, на границах которой наблюдались перелёт и недолёт. Эта вилка "половинилась" до достижения узкой вилки. Если объект был целью, на середине этой вилки давалась команда всем орудиям батареи на поражение.

После поражения цели или пристрелки репера следовала замечательная команда: "Стой! Записать...", по которой первый номер на щите орудия записывал пристрелянные установки по цели или реперу. Это делалось для того чтобы в последующем по близким (к поражённым) целям не производить трудоёмкие расчёты и пристрелку в полном объёме, а использовать принцип ассоциативных вычислений для переноса огня, изменяя известные "близкие" установки. Так обеспечивалась возможность с большой вероятностью захватывать новую цель сразу в узкую вилку.

Таким образом, на деле реализовалась самообучающаяся система управления "стреляющий + батарея", позволяющая накапливать и оперативно использовать знания по всей местности, на всём доступном пространстве ведения боя – для переноса огня от поражённых целей или пристрелянных реперов.

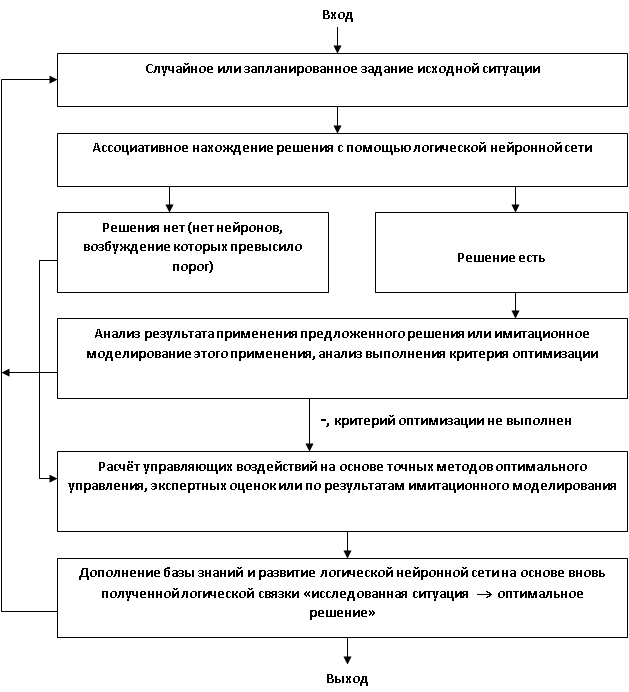
Рис. 13.7. Схема самообучения

Рассмотренный пример лежит в основе обобщения и построения развиваемой логической нейронной сети в составе самообучающейся системы управления и принятия решений. Подробно возможности и принципы построения самообучающихся систем управления изложены в [6 - 9]. Обобщим схему работы такой системы (рис. 13.7) в режиме обучения (подобно пристрелке реперов при занятии боевых позиций).

Работа многих сложных систем, особенно систем военного назначения, предполагает режим функционального контроля, когда система свободна от выполнения своих основных функций. В этом режиме и целесообразно развивать её базу знаний – до полного насыщения.

Очевидно, что база знаний для рассматриваемого применения по форме не отличается от базы знаний информационно-справочной системы и большинства СПР. Поэтому логическая нейронная сеть имеет вид, представленный на рис. 13.1, 13.2, 13.5, и 13.6, и использует те же функции активации нейронов. Возможно включение обратных связей, как на рис. 13.3, а также формирование "длинных" логических цепочек дедуктивного вывода, как на рис. 13.5.

Динамический выбор оптимальной стратегии распараллеливания в многопроцессорной вычислительной системе

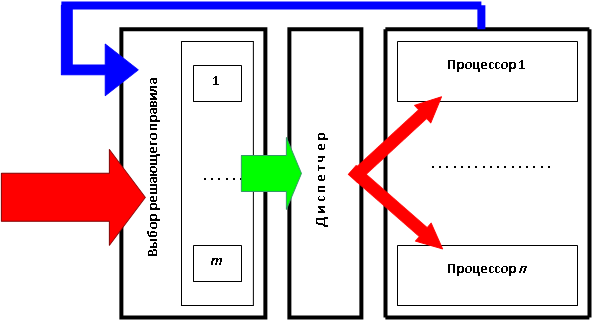
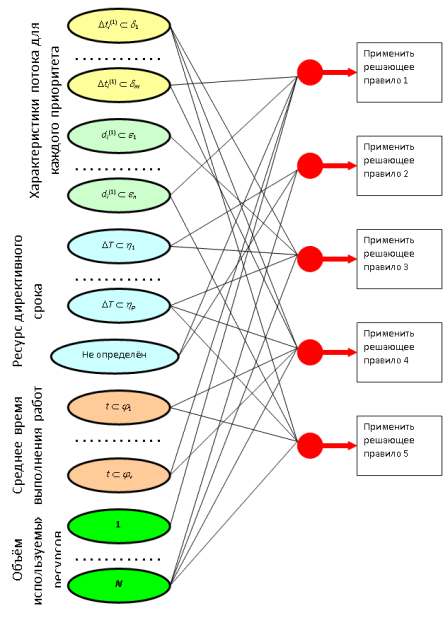
Рассмотрим обобщённую адаптивную схему динамического оптимизированного распределения потока задач между процессорами в многопроцессорной вычислительной системе или в сегменте вычислительной сети (рис. 13.8). Такая обработка характерна для Центра GRID-технологий [15]. Критерием оптимизации является достижение максимальной загрузки процессоров или выделенных сетевых ресурсов, служащей максимальной пропускной способности используемых вычислительных средств. В основе диспетчера, распределяющего поток запросов на решение задач, лежат несколько эвристических решающих правил, каждое из которых реализует некоторую стратегию распараллеливания. Решающие правила различаются по скорости реализации и по достигаемому эффекту в части статистических оценок обеспечения высокой пропускной способности. Выбор решающего правила и локализация его применения во времени зависят от характеристик потока запросов: от переменной плотности, от их типового состава, приоритета задач, частичной упорядоченности, директивных сроков решения.

Организация динамического распараллеливания вычислений – диспетчирование является основным трудоёмким и ответственным элементом построения управляемого вычислительного процесса в многопроцессорных вычислительных системах и вычислительных комплексах на основе сегментов ЛВС.

Поэтому, на данном этапе исследований, предположим, что динамическое распределение работ касается только потока задач виртуального управления сложными системами в реальном масштабе времени. Такие задачи образуют частично-упорядоченные множества и обладают наивысшим (первым) приоритетом. В этом случае задача диспетчирования становится трудно формализуемой. Оперативное управление текущим выбором стратегии необходимо производить с помощью логической нейронной сети, на рецепторный слой которой подаются текущие и пролонгированные характеристики потока запросов, а также текущие параметры состояния системы обслуживания. Нейроны выходного слоя максимальным возбуждением указывают на решающее правило, которым следует пользоваться в дальнейшем. То есть, максимально возбуждённый нейрон выходного слоя инициирует запуск соответствующей процедуры распределения в составе диспетчера.

Адаптация обеспечивается возможностью перезакрепления решающих правил за нейронами и вводом в рассмотрение новых правил – по статистическим оценкам эффективности распределения (распараллеливания).

Рис. 13.8. Схема адаптивного обслуживания потока задач

Рассмотренная схема легко развивается, модифицируется и специализируется.

Выделение неизменного состава характеристик, участвующих в принятии каждого решения, служит основой построения простейших по структуре однослойных логических нейронных сетей, где функция активации является аналогом конъюнкции и производит суммирование значений входных сигналов. На деле реализуется простейшая схема "голосования" в пользу той стратегии, которая в наибольшей степени адекватна сложившейся ситуации – текущим характеристикам потока запросов и состоянию системы обслуживания.

При этом основная трудность диспетчирования заключается в частичной упорядоченности (во времени выполнения) работ, которая присуща системам управления в реальном времени.

Диспетчер распараллеливания входит в состав операционной системы компьютера и сам по себе увеличивает "накладные расходы" производительности на собственную реализацию во времени. Поэтому быстродействие диспетчера представляет важнейшее требование к нему.

Другим требованием, предъявляемым к диспетчеру распараллеливания, является достаточная близость формируемых им планов к точным оптимальным, полученным на основе решения задачи распараллеливания в адекватной постановке.

Дело в том, что решаемая диспетчером задача относится к важному классу задач исследования операций [15] – к классу задач параллельного программирования. Это задачи экспоненциальной сложности (NP-сложные задачи). Решение таких задач для множеств частично упорядоченных работ весьма трудоёмко и никак не может быть положено в основу программ операционной системы компьютера. Поэтому прибегают к эвристическим методам полиномиальной сложности (Р-сложность) для оперативного, динамического распараллеливания. В основе таких методов можно выделить одно или более решающих правил, погружённых в алгоритм распараллеливания и обусловленных предпочтительным выбором альтернативы в ключевых ситуациях.

Применение каждого решающего правила при распараллеливании влечёт различный объём вычислений – накладных расходов. Однако, как правило, увеличение сложности алгоритмов распараллеливания обусловлено попытками приблизить результаты планирования к точным оптимальным. Поэтому, по результатам достаточного опыта, можно считать, что более трудоёмкий диспетчер статистически обеспечивает планы параллельного выполнения работ, более близкие к оптимальным.

При практическом решении задач распараллеливания ограничиваются однородными системами выделяемых средств (однородными вычислительными системами [15]), а различные подходы к диспетчированию отличаются вариантами единственного решающего правила.

По трудоёмкости, а, следовательно, "по оптимальности", варианты решающего правила можно упорядочить:

Из множества работ, выполнение которых может начаться в текущий момент времени, назначение на свободные процессоры следует производить произвольно (по сложившемуся порядку номеров, первую в списке, случайно и т.д.).
Из множества работ, выполнение которых может начаться в текущий момент времени, назначение на свободные процессоры следует производить в порядке не возрастания времени выполнения работ (в первую очередь назначать работу с максимальной оценкой времени выполнения).
Из множества работ, выполнение которых может начаться в текущий момент времени, в первую очередь на свободный компьютер (процессор) назначать работу, предшествующую максимальному объёму непосредственно или транзитивно следующих ей работ, включая её саму.
При известном директивном сроке выполнения комплекса работ (в том числе – в системе реального времени), из множества работ, выполнение которых может начаться в текущий момент времени, назначать на свободный компьютер (процессор) работу, обладающую минимальным значением позднего срока окончания выполнения.
В дополнение к 4: При равных минимальных значениях позднего срока окончания выполнения в первую очередь назначить работу в соответствии с правилом 3.

В различных случаях применения эффективно используются и другие комбинации решающих правил 2, 3, 4.

Первое и второе решающие правила используются в динамических диспетчерах, предполагающих выполнение назначенных работ одновременно с дальнейшим планированием.

Третье и последующие решающие правила предполагают работу диспетчера вне времени выполнения назначенных работ: диспетчер разрабатывает план выполнения этих работ, затем этот план реализуется без включения диспетчера. Это обеспечивает плотную загрузку процессоров при выполнении работ и, следовательно, их скорейшее освобождение – переход в свободный ресурс.

Очевидно, что чем большим ресурсом времени обладает диспетчер в связи с "разреженным" потоком высокоприоритетных заданий при заданных директивных сроках выполнения, тем больше искушение использовать решающие правила для распределения этих заданий, приближающие результаты планирования к оптимальным. Ведь при этом достигается минимальное время выполнения совокупности взаимозависимых работ, плотно загружаются процессоры, выделяется время для фонового выполнения запросов с меньшим приоритетом.

Это справедливо, если одновременное увеличение накладных расходов на планирование в совокупности с разработанным планом всё же служит оптимизации параллельного вычислительного процесса, то есть, минимизации времени выполнения комплекса работ высокого приоритета.

С другой стороны, очевидно, что при плотном потоке заданий высокого приоритета требование их оперативного распределения между вычислительными средствами заслоняет собой все другие требования к оптимизации вычислительного процесса. Становится не до оптимизации: ведь плотная загрузка всех средств и так гарантирована! В этом случае достаточно использовать простейшее решающее правило.

Таким образом, только на основе моделирования и опытных исследований, для достаточного числа точек факторного пространства – характеристик потоков заданий, их временных характеристик, директивных сроков их выполнения, требуемых ресурсов и состояния загрузки вычислительных средств, – можно получить ряд рекомендаций по применению решающих правил в диспетчере распараллеливания.

Общий вид логической нейронной сети, реализующей диспетчер, представлен на рис. 13.9.

Директивный срок Т определяется, как длина отрезка времени, через которое распределяемое множество частично упорядоченных работ должно быть выполнено обязательно. Например, Т – длительность такта системы управления. Ресурс директивного срока при планировании распараллеливания определяется как разность,

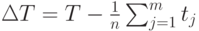$\Delta T=T-\frac{1}{n}\sum_{j=1}^{m}t_j$ ,где п – число выделенных процессоров, m – количество распределяемых работ, t_j – время решения задачи.

На рисунке:

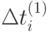$\Delta t_i^{(1)}$ – усреднённое по серии последних запросов время между запросами высшего, 1-го приоритета;

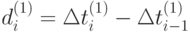$d_i^{(1)} = \Delta t_i^{(1)} - \Delta t_{i-1}^{(1)}$ – аналог первой производной.

Таким образом, на рецепторном слое указывается вероятность принадлежности характеристик интервалам 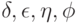$\delta, \epsilon, \eta, \phi$ значений или значениям. Максимальное возбуждение нейрона выходного слоя (при высоком пороге) указывает на необходимость автоматического включения соответствующего решающего правила в диспетчер.

Возможность оптимизации совместной реализации запросов на выполнение нескольких частично упорядоченных работ предполагает частичное или полное накопление этих запросов (работ) в некотором "окне просмотра" диспетчера. Диспетчер с высокой частотой анализирует содержимое "окна просмотра", пытаясь "уложить" выполнение этих работ за минимальное время, не превышающее директивный срок Т. Время выполнения запросов, а также время работы диспетчера, измеряется условными единицами. Временные оценки известны заранее.

увеличить изображение
Рис. 13.9. Примерный вид логической нейронной сети диспетчера

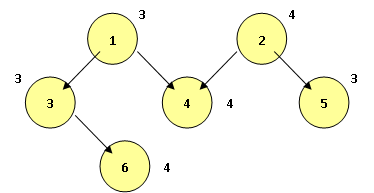
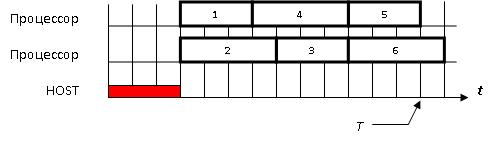
Пример. Пусть для выполнения работ выделены два процессора суперкомпьютера. Диспетчер реализован на управляющем HOST-процессоре. В "окне просмотра" накопились работы, порядок следования которых можно описать информационным графом (рис. 13.10).

Рис. 13.10. Информационный граф

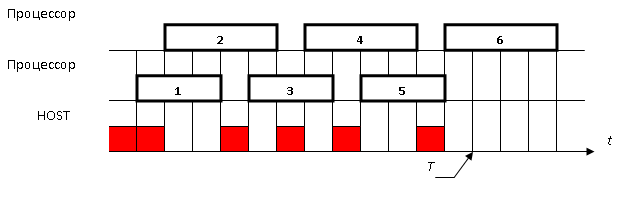
Пусть диспетчер использует решающее правило 1. Время его однократного выполнения составляет 1 у.е., Т = 13 у.е. Тогда временная диаграмма выполнения комплекса работ представлена на рисунке 13.11.

Рис. 13.11. Временная диаграмма выполнения работ с решающим правилом 1

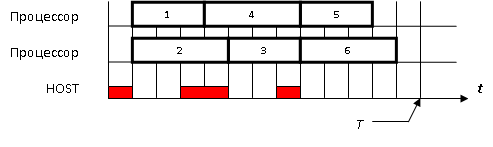
Для диспетчера, использующего решающее правило 2, временная диаграмма выполнения того же комплекса работ на двух процессорах представлена на рисунке 13.12.

Рис. 13.12. Временная диаграмма выполнения работ с решающим правилом 2

Для диспетчера, реализующего решающее правило 4, при том же директивном сроке окончания выполнения, временная диаграмма представлена на рис. 13.13. Время однократной работы диспетчера для двух выделенных процессоров выбрано равным 3 у.е.

Рис. 13.13. Временная диаграмма выполнения работ c решающим правилом 4

Краткие итоги

Может показаться, что предлагаемый здесь способ "бесформульных" вычислений представляет собой лишь сложную интерпретацию табличного метода. Однако применение логических нейронных сетей позволяет осуществить:
- Переход к нечётким, то есть к недостоверным данным;
- Совместное использование данных и объектов разных типов и свойств;
- Выполнение интерполяции (экстраполяции) на основе нахождения среднего, допускающей рассмотрение большого числа решений, на которые указывают нейроны, возбуждение которых превысило порог;
- Любое увеличение длины исследуемых векторов без существенного влияния на вычислительную нагрузку. При увеличении размерности задачи возрастает лишь объём базы знаний;
Схема ситуационного управления легко трансформируется в схему "бесформульных" вычислений. Включение в неё точной модели управляемого процесса (при невозможности натурных экспериментов) позволяет получить самообучающуюся систему управления. Нейросетевое воплощение обеспечивает малую сложность алгоритмов управления и высокую реальную производительность вычислительных средств в рабочем режиме.
Не ищите способы непосредственного получения расписания использования ресурсов методами, позволяющими производить лишь оценки. Расписания, в том числе оптимальные, получаются лишь при численном решении задач планирования. Выбор решающих правил, лежащих в основе приближённых, эвристических алгоритмов планирования, может производиться динамически на основе оценки складывающейся обстановки и её прогнозирования. Логическая нейронная сеть при этом способна быть хорошим помощником.

Вопросы.

На чём основана идея "бесформульных" вычислений и как она реализуется с помощью логической нейронной сети?
Как осуществляется ситуационное управление?
Как идеи ситуационного управления развиваются для построения самообучающихся систем управления?
Как реализуется самообучающаяся система управления с помощью логической нейронной сети?
В чём заключается способ учёта текущих и прогнозируемых характеристик потока запросов при выборе оптимального плана их параллельного (многоканального) обслуживания?
Как производится настройка (адаптация) диспетчера оптимального распараллеливания по текущим и прогнозируемым характеристикам потока запросов?

Дальше >>

Авторизоваться

Нейросетевые технологии искусственного интеллекта

Обучаемые и самообучающиеся системы распознавания, управления и принятия решений на логических нейронных сетях