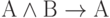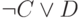Основы математической логики
Исчисление высказываний
Предметом дальнейших исследований примем любое законченное утверждение на любом формальном или неформальном языке - высказывание, для которого имеет смысл говорить о его истинности или ложности. Это было уже объявлено в Лекции 1.
Основной задачей, которую ставит перед собой математическая логика, является формализация мыслительных процессов в широком смысле - в смысле доказательства или поиска истины, а также расширения знаний. Для этого надо сформулировать "правильное", непротиворечивое логическое исчисление, включающее:
- Формализацию представления высказываний;
- Набор операций, позволяющий создавать формулы, как более сложные высказывания на базе более простых;
- Аксиомы и правила вывода, позволяющие выводить логические следствия из любой заданной системы высказываний и формально характеризовать тождественно истинные высказывания и формулы.
Тождественно истинными являются высказывания, которые не требуют задания каких-либо дополнительных условий для проверки своей истинности на протяжении всего процесса логического вывода.
Например, высказывание "кислород является газом" имеет значение ИСТИНА (1) в тех условиях, в которых оно рассматривается. Ведь кислород может находиться не только в газообразном состоянии.
Высказывание "дважды два - одиннадцать" на первый взгляд представляется заведомо ложным. Однако если предположить, что вместо десятичной системы счисления используется троичная система, при условии сохранения привычных названий многозначных чисел, то данное высказывание становится истинным.
Поэтому обязательным условием правильности выводов и следствий является то, чтобы постоянное высказывание, подобно константе, не меняло значение истинности в процессе логического вывода.
В исчислении высказываний не интересуются внутренней смысловой структурой элементарных высказываний. Естественно поэтому для их обозначения использовать отдельные буквы некоторого алфавита (обычно латинского и готического). Отдельными буквами могут обозначаться и так называемые переменные высказывания, что означает, что вместо этой буквы всегда может быть подставлено любое конкретное постоянное высказывание, как истинное, так и ложное.
Высказывания, как постоянные, так и переменные, можно объединять в сложные высказывания, используя связки "и", "или", "если - то", "не" и т.п. Если в состав сложного высказывания входят переменные высказывания, представленные буквами, то при замене этих букв одними высказываниями сложное высказывание может оказаться истинным, а при замене другими - ложными. Например, сложное высказывание "А и В", где А и В - переменные высказывания, будет, очевидно, истинным в том и только том случае, если оба высказывания будут истинными.
Существуют и такие сложные высказывания, содержащие в своём составе переменные высказывания, которые остаются истинными при любых значениях переменных высказываний. Например, сложное высказывание "если неверно то, что высказывание А ложно, то высказывание А истинно" остаётся истинным, какое бы высказывание ни подставили на место переменного высказывания А. Такие высказывания называют тождественно истинными.
Например, возьмём высказывание "извозчик Петров - водитель кобылы". Если неверно то, что Петров не водитель кобылы, значит он водитель кобылы. Сложное высказывание истинно. Если же неверно, что Петров водитель кобылы, значит он не водитель кобылы. Сложное высказывание снова истинно, ибо соответствует правде и не содержит противоречий.
Задача выделения тождественно истинных высказываний во множестве всех возможных высказываний является важнейшей задачей любого логического исчисления.
После всех предварительных замечаний перейдём к построению собственно исчисления высказываний, или, как его ещё иногда называют, пропозиционного исчисления.
Введём базовые операции.
-
Конъюнкция двух высказываний образует новое высказывание
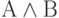 , которое является истинным тогда и только тогда, когда А и В истинны. В обычной речи этой операции соответствует связка "и".
, которое является истинным тогда и только тогда, когда А и В истинны. В обычной речи этой операции соответствует связка "и". -
Дизъюнкция
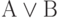 образует новое высказывание, которое истинно тогда и только тогда, когда истинно хотя бы одно высказывание А или В. Однако, хотя мы уже применили связку "или", под ней понимается не разделительное "или", понимаемое в смысле "либо - либо", когда А и В не могут быть оба истинны. В данном определении высказывание
образует новое высказывание, которое истинно тогда и только тогда, когда истинно хотя бы одно высказывание А или В. Однако, хотя мы уже применили связку "или", под ней понимается не разделительное "или", понимаемое в смысле "либо - либо", когда А и В не могут быть оба истинны. В данном определении высказывание 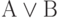 истинно и при истинности обоих высказываний А и В.
истинно и при истинности обоих высказываний А и В. - Высказывание
 ложно тогда и только тогда, когда А истинно, а В ложно. А называется посылкой, а В - следствием. В обычной речи операция
ложно тогда и только тогда, когда А истинно, а В ложно. А называется посылкой, а В - следствием. В обычной речи операция 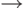 (импликация) соответствует связке "если - то": "если А, то В". В определении математической логики это высказывание при ложном А всегда истинно, независимо от того, истинно или ложно высказывание В. Этот факт можно кратко сформулировать так: "из ложного следует всё что угодно". В обычной речи иногда подразумевается, что когда А ложно, то высказывание "если А, то В" не имеет смысла. (Порой кажется, что принятый формализм прямо-таки противоречит здравому смыслу. Например, высказывание "из того, что у льва есть когти, следует, что снег белый" формально истинно. Но так ли это в действительности, решать не математикам-логикам.)
(импликация) соответствует связке "если - то": "если А, то В". В определении математической логики это высказывание при ложном А всегда истинно, независимо от того, истинно или ложно высказывание В. Этот факт можно кратко сформулировать так: "из ложного следует всё что угодно". В обычной речи иногда подразумевается, что когда А ложно, то высказывание "если А, то В" не имеет смысла. (Порой кажется, что принятый формализм прямо-таки противоречит здравому смыслу. Например, высказывание "из того, что у льва есть когти, следует, что снег белый" формально истинно. Но так ли это в действительности, решать не математикам-логикам.) - Операция отрицание
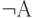 формирует ложное высказывание, если А истинно, и истинное, если А ложно.
формирует ложное высказывание, если А истинно, и истинное, если А ложно. - Высказывание
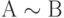 истинно тогда и только тогда, когда А и В оба истинны или оба ложны. Это высказывание называется эквивалентностью.
истинно тогда и только тогда, когда А и В оба истинны или оба ложны. Это высказывание называется эквивалентностью.
Как и в булевой алгебре, значение ИСТИНА будем обозначать единицей, значение ЛОЖЬ - нулём.
В табл. 3.2 сведены соотношения истинности для базовых операций.
| А | В | 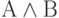 |
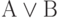 |
 |
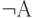 |
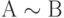 |
|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 | 1 | 0 |
| 0 | 0 | 0 | 0 | 1 | 1 | 1 |
Как и в булевой алгебре введём ранжирование операций: 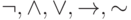 .
.
Например, формула  понимается как
понимается как  . Формула
. Формула 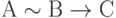 должна пониматься как
должна пониматься как 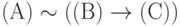 и т.д.
и т.д.
Введённые определения решают лишь две части задачи построения исчисления высказываний: проблему формализации записи сложных высказываний.
Завершающая часть задачи - нахождение способа определения тождественной истинности высказываний - может быть решена двумя путями: содержательным и формальным.
При содержательном подходе необходимо помнить о содержательном смысле букв и связок. В то же время, нет необходимости помнить само высказывание, достаточно помнить функцию истинности этого высказывания: А = ИСТИНА, если высказывание, обозначенное этой буквой, истинно, и А = ЛОЖЬ, если высказывание ложно. Функция истинности отождествляется с самой буквой, которая теперь обозначает булеву переменную.
Тогда каждую формулу  исчисления высказываний можно интерпретировать как формулу в булевой алгебре с включённой в неё дополнительно операцией импликации
исчисления высказываний можно интерпретировать как формулу в булевой алгебре с включённой в неё дополнительно операцией импликации 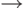 . Входящие в формулу
. Входящие в формулу  постоянные высказывания должны быть заменены соответствующими булевыми константами (значениями их функций истинности). Символы, соответствующие переменным высказываниям, рассматриваются как аргументы булевой функции, представляемой формулой
постоянные высказывания должны быть заменены соответствующими булевыми константами (значениями их функций истинности). Символы, соответствующие переменным высказываниям, рассматриваются как аргументы булевой функции, представляемой формулой  . Эта функция называется функцией истинности сложного высказывания, выражаемого формулой
. Эта функция называется функцией истинности сложного высказывания, выражаемого формулой  .
.
На содержательном уровне построения исчисления высказываний тождественно истинными считаются те, и только те формулы этого исчисления (сложные высказывания), функции истинности которых принимают значения ИСТИНА (1) при всех значениях переменных.
Представленный содержательный аспект исчисления высказываний позволяет сравнительно просто решить вопрос о тождественной истинности любого сложного высказывания: достаточно перебрать все возможные наборы значений истинности составляющих его переменных высказываний и проверить, на всех ли этих наборах функция истинности рассматриваемого сложного высказывания принимает значение ИСТИНА.
Например, рассмотрим формулу  и составим для неё таблицу истинности с учётом "промежуточного" результата
и составим для неё таблицу истинности с учётом "промежуточного" результата 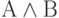 :
:
Видим, что при всех значениях переменных высказываний, сложное высказывание является истинным. Следовательно, рассмотренная формула  тождественно истинная.
тождественно истинная.
Несмотря на простоту и "прозрачность", содержательный аспект исчисления высказываний имеет ряд недостатков:
- Он не может использоваться в других исчислениях, где множество аргументов может быть бесконечным.
- Ему свойственна недостаточная формализация процесса доказательства и самого понятия доказательства истинности тех или иных формул.
При формальном подходе к установлению тождественной истинности пользуются эквивалентными преобразованиями булевой алгебры. Поскольку там нет импликации, исключим её согласно равенству:
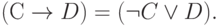 |
( 3.24) |
Проверим его справедливость с помощью таблицы истинности:
Рассмотрим тот же пример:
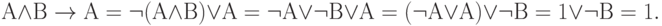
Эта цепочка доказывает тождественную истинность заданной формулы.
Таким образом, формальный аспект исчисления высказываний характеризуется тем, что полностью отвлекаются от содержательного смысла формул и рассматривают их как конечные последовательности символов, подлежащие эквивалентным преобразованиям.
Для этих преобразований, подобно и в дополнение базовому набору соотношений булевой алгебры, известна наиболее употребительная система аксиом С.К. Клини:
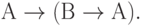
( 3.25) 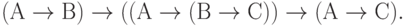
( 3.26) 
( 3.27) 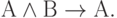
( 3.28) 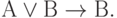
( 3.29) 
( 3.30) 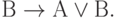
( 3.31) 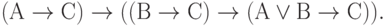
( 3.32) 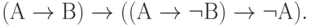
( 3.33) 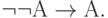
( 3.34) 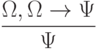
( 3.35)
Первые десять аксиом представляют собой десять формул исчисления высказываний, объявленных тождественно истинными по определению. Они предполагают возможность подстановки вместо букв А, В, С любых формул исчисления высказываний (не обязательно истинных). Такая подстановка, по определению, не нарушает тождественной истинности аксиомы.
Одиннадцатая аксиома - это так называемое правило вывода, позволяющее, по определению, считать доказанной истинность формулы  , если истинность формул
, если истинность формул  и
и 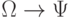 уже была установлена ранее. Если формулы
уже была установлена ранее. Если формулы  и
и 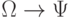 были при этом тождественно истинными. То тождественно истинной будет и формула
были при этом тождественно истинными. То тождественно истинной будет и формула  . Предполагается по определению, что все тождественно истинные формулы (и только такие формулы) исчисления высказываний могут быть получены из аксиом в результате подстановок 1 - 10 и применения (возможно, многократного) правил вывода 11.
. Предполагается по определению, что все тождественно истинные формулы (и только такие формулы) исчисления высказываний могут быть получены из аксиом в результате подстановок 1 - 10 и применения (возможно, многократного) правил вывода 11.
Формула  называется непосредственным следствием формул
называется непосредственным следствием формул  и
и 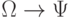 .
.
Формулы, тождественно истинные в содержательном смысле, для краткости будем называть просто содержательно истинными, противопоставляя их формально истинным, т.е. формально доказуемым.
Говорят, что формула  исчисления высказывания выводится из условно истинных формул (истинность которых предполагается на протяжении рассматриваемого вывода)
исчисления высказывания выводится из условно истинных формул (истинность которых предполагается на протяжении рассматриваемого вывода) 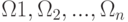 , если она может быть получена из этих формул и аксиом 1 - 10 исчисления высказываний в результате применения конечного числа раз правил непосредственного следствия.
, если она может быть получена из этих формул и аксиом 1 - 10 исчисления высказываний в результате применения конечного числа раз правил непосредственного следствия.
Более точно это означает последовательное использование трёх условий, лежащих в основе правил вывода:
- Любая из формул
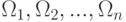 выводима на основе аксиом.
выводима на основе аксиом. - Любая аксиома из 1 - 10 (с учётом возможности подстановки любых формул вместо входящих в них букв) выводима.
- Если формулы
 и
и 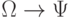 выводимы, то выводимой будет также формула
выводимы, то выводимой будет также формула  .
.
Цепочка формул, получающихся в результате последовательного применения этих трёх правил, которая кончается формулой  , называется формальным выводом этой формулы.
, называется формальным выводом этой формулы.
Для обозначения выводимости употребляется специальный символ \vdash (читается как "даёт"), слева от которого пишутся условно истинные формулы, а справа их следствия: 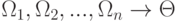 . Аксиомы здесь как бы включаются в символ
. Аксиомы здесь как бы включаются в символ 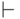 . Тогда для любой формально истинной формулы
. Тогда для любой формально истинной формулы  , выводимой только лишь на основе аксиом 1 - 10, можно писать
, выводимой только лишь на основе аксиом 1 - 10, можно писать 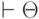 .
.
Приведём простейшие примеры формального вывода, нумеруя последовательные шаги.
-
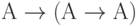 (аксиома 1, в которой буква В заменена буквой А).
(аксиома 1, в которой буква В заменена буквой А). -
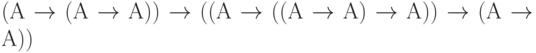 (аксиома 2, в которой буква В заменена формулой
(аксиома 2, в которой буква В заменена формулой  , а буква С - буквой А).
, а буква С - буквой А). -
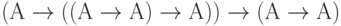 (применение правила вывода 11 к формулам, полученным на шагах 1 и 2).
(применение правила вывода 11 к формулам, полученным на шагах 1 и 2). -
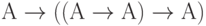 (аксиома 1, в которой буква В заменена формулой (
(аксиома 1, в которой буква В заменена формулой ( )).
)). -
 (применение правила вывода 11 к формулам, полученным на предыдущих двух шагах
(применение правила вывода 11 к формулам, полученным на предыдущих двух шагах
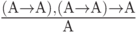
( 3.36)
Приведённая цепочка формул по определению является формальным доказательством формулы  . Таким образом, эта формула принадлежит к числу формально истинных формул, и её можно записать
. Таким образом, эта формула принадлежит к числу формально истинных формул, и её можно записать

Другим примером является получение следствий из трёх условно истинных формул 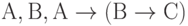 . За пять шагов из этих формул может быть получена формула С.
. За пять шагов из этих формул может быть получена формула С.
- А (первая данная нам условно истинная формула).
- В (вторая данная нам формула).
-
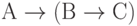 (третья данная нам формула).
(третья данная нам формула). -
 (непосредственное следствие по правилу вывода 11 их формул 1 и 2).
(непосредственное следствие по правилу вывода 11 их формул 1 и 2). - С (непосредственное следствие формул 2 и 4).
Таким образом, формула С выводима из формул 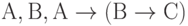 и мы можем записать
и мы можем записать 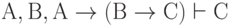 .
.
Хотя условно истинные формулы и не обладают тождественной истинностью, легко видеть, что в окончательной записи (условной) выводимости любая буква может быть заменена произвольной формулой, если только такая замена производится как слева, так и справа от знака  .
.
Подобным же способом можно доказать соотношения:
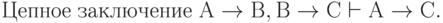
( 3.37) 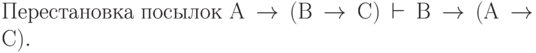
( 3.38) 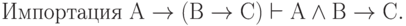
( 3.39) 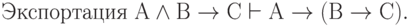
( 3.40) 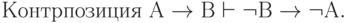
( 3.41) 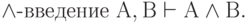
( 3.42) 
( 3.43)
Обозначим 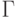 произвольную конечную совокупность формул исчисления высказываний. Применяя более сложную технику доказательства (индукцию по длине вывода), можно доказать следующую теорему о дедукции.
произвольную конечную совокупность формул исчисления высказываний. Применяя более сложную технику доказательства (индукцию по длине вывода), можно доказать следующую теорему о дедукции.
Теорема 3.1. Если в исчислении высказываний формула В выводима из совокупности формул 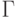 и А, то из
и А, то из 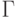 выводима формула
выводима формула  .
.
В теории доказательств часто применяются две общие схемы.
- Доказательство путём разбора случаев: если
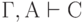 и
и 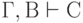 , то
, то
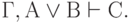
( 3.44) - Приведение к абсурду: если
 и
и 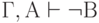 , то
, то
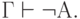
( 3.45)
Легко проверить, что все аксиомы исчисления высказываний 1 - 10 представляют собой содержательно истинные формулы. Иначе говоря, соответствующие им функции истинности принимают при всех значениях переменных значение ИСТИНА. Это свойство, очевидно, сохраняется при подстановках любых формул исчисления высказываний вместо букв, входящих в аксиомы.
Из таблицы истинности для импликации 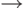 непосредственно следует, что из содержательной истинности формул
непосредственно следует, что из содержательной истинности формул  и
и 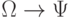 вытекает содержательная истинность формулы
вытекает содержательная истинность формулы  . Но тогда очевидно, что все доказуемые (формально истинные) формулы будут и содержательно истинными. Верно (хотя и гораздо сложнее доказуемо) также и обратное, что формулируется следующей теоремой.
. Но тогда очевидно, что все доказуемые (формально истинные) формулы будут и содержательно истинными. Верно (хотя и гораздо сложнее доказуемо) также и обратное, что формулируется следующей теоремой.
Теорема 3.2. При формальном построении исчисления высказываний с помощью системы аксиом 1 - 11 формально доказуемыми (формально истинными) будут все те, и только те формулы этого исчисления, которые являются тождественно истинными в содержательном смысле.
Теорема 2 содержит в себе два утверждения относительно выбранной системы аксиом: эта система содержательно непротиворечива и эта система содержательно полна, т.е. нет ни одной содержательно истинной формулы исчисления высказываний, которую нельзя было бы доказать формально с помощью этой системы аксиом.
При этом, естественно называть систему аксиом формально непротиворечивой, если с её помощью нельзя вывести какую-нибудь формулу  вместе с её отрицанием
вместе с её отрицанием 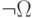 ; в противном случае она формально противоречива.
; в противном случае она формально противоречива.
Отметим, что хотя присоединение недоказуемых формул в качестве новых аксиом исчисления высказываний, нарушает свойство формальной непротиворечивости, ничто не мешает нам присоединить к системе аксиом формулы 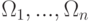 в качестве не тождественно, а лишь условно истинных формул. (Это характерно, например, при переходе в мир грёз или сказок.) Противоречие возникает тогда и только тогда, когда конъюнкция
в качестве не тождественно, а лишь условно истинных формул. (Это характерно, например, при переходе в мир грёз или сказок.) Противоречие возникает тогда и только тогда, когда конъюнкция 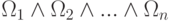 является тождественно ложной формулой.
является тождественно ложной формулой.