Передача информации
Особенности векторных пространств над конечным полем GF(2). Линейный групповой код
Одним из подходов к регулярному построению кодов является применение в качестве кодовых множеств линейных подпространств [29], [33], [34]. Одно из преимуществ такого подхода заключается в хорошо изученной структуре подпространств линейных векторных пространств.
Для построения кодов, обнаруживающих и исправляющих ошибки, используются векторные пространства над конечным полем 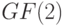 [32]. В этом случае множество (
[32]. В этом случае множество ( -мерный куб)
-мерный куб)  рассматривается как линейное векторное пространство над конечным полем
рассматривается как линейное векторное пространство над конечным полем 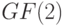 . Точки из
. Точки из  становятся векторами, их можно складывать и умножать на числа из поля
становятся векторами, их можно складывать и умножать на числа из поля 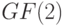 .
.
Специфика некоторых понятий линейной алгебры в векторном пространстве  является следствием особенностей поля
является следствием особенностей поля 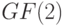 . Сложение векторов из
. Сложение векторов из  производится покоординатно с учетом особенностей операции сложения в поле
производится покоординатно с учетом особенностей операции сложения в поле 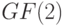 .
.
Сложение и умножение в поле определяется следующими таблицами.
Сложение в поле 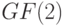 (сложение по модулю 2) часто обозначается
(сложение по модулю 2) часто обозначается  . Этим же знаком будем обозначать сложение векторов из
. Этим же знаком будем обозначать сложение векторов из  . Следует отметить справедливое для всех векторов
. Следует отметить справедливое для всех векторов 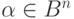 равенство
равенство 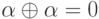 , вытекающее из таблицы сложения. Оно означает, что любой вектор является противоположным себе
, вытекающее из таблицы сложения. Оно означает, что любой вектор является противоположным себе 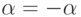 , а также что при заданных
, а также что при заданных  и (
и ( уравнение имеет решение
уравнение имеет решение 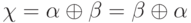 .
.
Рассмотрим особенности еще некоторых понятий линейной алгебры.
Линейная комбинация в  . Учитывая, что
. Учитывая, что  рассматривается как векторное пространство над конечным полем
рассматривается как векторное пространство над конечным полем 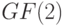 , содержащим только два элемента 0 и 1, линейная комбинация в
, содержащим только два элемента 0 и 1, линейная комбинация в  превращается в сумму векторов
превращается в сумму векторов
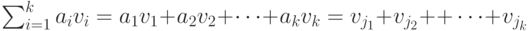
Линейная оболочка множества векторов из 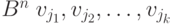 - это совокупность различных сумм этих векторов. Линейная оболочка векторов
- это совокупность различных сумм этих векторов. Линейная оболочка векторов 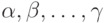 будет обозначаться через
будет обозначаться через ![[\alpha, \beta, \dots, \gamma]](/sites/default/files/tex_cache/f6813a2315e3d6fb06779f0610598fb5.png) .
.
Линейная зависимость векторов из  . Векторы
. Векторы 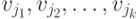 линейно зависимы, если существует сумма некоторых из них, равная 0.
линейно зависимы, если существует сумма некоторых из них, равная 0.
Векторы 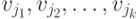 линейно независимы, если любая сумма некоторых из них не равна 0.
линейно независимы, если любая сумма некоторых из них не равна 0.
Утверждение. Если векторы 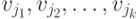 независимы, то все их линейные комбинации (суммы) различны.
независимы, то все их линейные комбинации (суммы) различны.
Доказательство. Предположим, что  Удалив из левой и правой частей этого равенства одинаковые векторы и перенеся оставшиеся из правой части в левую, получим нулевую сумму векторов. Это противоречит их линейной независимости.
Удалив из левой и правой частей этого равенства одинаковые векторы и перенеся оставшиеся из правой части в левую, получим нулевую сумму векторов. Это противоречит их линейной независимости.
Всего из  линейно независимых векторов можно составить
линейно независимых векторов можно составить
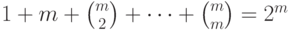
линейных комбинаций, и все они различны.
Из доказанного утверждения следует, что линейная оболочка  линейно независимых векторов содержит
линейно независимых векторов содержит 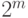 вектора.
вектора.
Рассмотрим пример. Пусть имеем два вектора
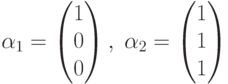
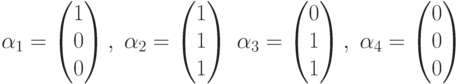
Их линейная оболочка ![[\alpha_1, \alpha_2]](/sites/default/files/tex_cache/1e1e605265d66562f70039ffd7fdb83a.png) состоит из четырех векторов На традиционном изображении
состоит из четырех векторов На традиционном изображении 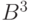 в виде точек куба
в виде точек куба 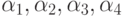 образуют плоскость (увеличенные светлые вершины куба на рисунке).
образуют плоскость (увеличенные светлые вершины куба на рисунке).
Подпространства в  . Подпространством векторного пространства
. Подпространством векторного пространства  называется подмножество векторов из
называется подмножество векторов из  , замкнутое относительно операций сложения и умножения на число из поля
, замкнутое относительно операций сложения и умножения на число из поля 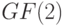 . Линейная оболочка
. Линейная оболочка ![[\alpha, \beta, \dots \gamma]](/sites/default/files/tex_cache/282af775e574f81cc695f1580541d771.png) векторов
векторов 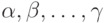 уявляется подпространством пространства
уявляется подпространством пространства  .
.
Например, рассмотренная в предыдущем примере линейная оболочка из четырех векторов является подпространством, а множество векторов
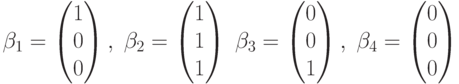
подпространством не является, поскольку оно не замкнуто относительно операции сложения. Например,  не входит в это множество векторов.
не входит в это множество векторов.
По аналогии с подпространствами в 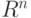 подпространства в
подпространства в  могут задаваться системами линейных уравнений (но над полем
могут задаваться системами линейных уравнений (но над полем 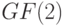 ). Именно таким образом далее будет задаваться линейный групповой код.
). Именно таким образом далее будет задаваться линейный групповой код.
Нормой вектора 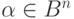 называется число
называется число  единичных координат этого вектора. В кодировании норму вектора называют также весом этого вектора. С помощью нормы вектора и операции сложения векторов в
единичных координат этого вектора. В кодировании норму вектора называют также весом этого вектора. С помощью нормы вектора и операции сложения векторов в  (операции покоординатного сложения по
(операции покоординатного сложения по 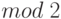 ) выражение для расстояния Хеминга может быть записано в виде
) выражение для расстояния Хеминга может быть записано в виде

Кодовое расстояние линейного кода может быть вычислено проще, чем кодовое расстояние произвольного кода. Учитывая, что для слов 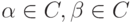 линейного кода
линейного кода 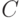 справедливо
справедливо 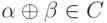 , выполняется следующая цепочка равенств
, выполняется следующая цепочка равенств

Определение. Пусть 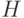 - матрица над полем
- матрица над полем 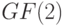 размера
размера 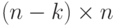 и ранга
и ранга 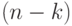 . Множество
. Множество  решений уравнения
решений уравнения 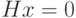 называется линейным
называется линейным 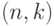 кодом.
кодом. 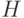 - проверочная матрица,
- проверочная матрица,  - длина кода,
- длина кода,  - размерность кода. Если матрица
- размерность кода. Если матрица 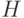 имеет вид
имеет вид 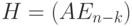 , где
, где 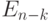 - единичная матрица порядка
- единичная матрица порядка 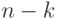 , то код называется систематическим.
, то код называется систематическим.
Построение линейного кода по заданной порождающей матрице
Рассмотрим, как можно получить линейный код, зная порождающую матрицу. Для этого решим уравнение 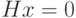 и найдем кодовые слова. В матричном виде уравнение для кодовых слов запишется в виде
и найдем кодовые слова. В матричном виде уравнение для кодовых слов запишется в виде
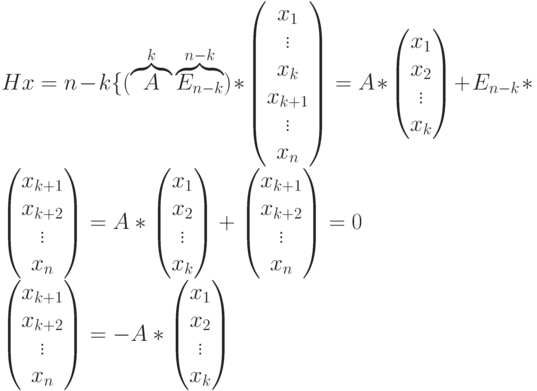 |
( 7.1) |
Чтобы найти решение, нужно произвольно задать  компонент
компонент 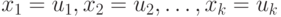 вектора
вектора  , а остальные вычислить по формуле (2.6). Таким образом, первые
, а остальные вычислить по формуле (2.6). Таким образом, первые  компонент вектора
компонент вектора  полностью его определяют
полностью его определяют
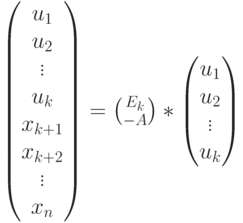 |
( 7.2) |
Матрица 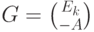 называется порождающей. Ее столбцы образуют базис пространства решений системы
называется порождающей. Ее столбцы образуют базис пространства решений системы 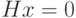 . Учитывая особенности поля
. Учитывая особенности поля 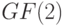 , порождающая матрица имеет вид
, порождающая матрица имеет вид 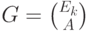 .
.
Нетрудно показать, что справедливо равенство 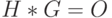 , где
, где  - матрица из нулевых элементов, имеющая
- матрица из нулевых элементов, имеющая 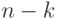 строк и
строк и  столбцов.
столбцов.
Для того чтобы лучше понять свойства линейных кодов, полезно рассматривать произведение 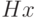 как линейную комбинацию столбцов
как линейную комбинацию столбцов 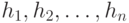 матрицы
матрицы 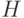 с коэффициентами, являющимися компонентами вектора
с коэффициентами, являющимися компонентами вектора  .
.
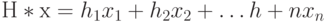
Свойства линейных кодов зависят от проверочной матрицы. Эта зависимость описывается следующей леммой [34].
Лемма. Линейный код 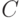 с проверочной матрицей
с проверочной матрицей 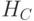 имеет кодовое расстояние
имеет кодовое расстояние 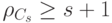 тогда и только тогда, когда любые s столбцов матрицы
тогда и только тогда, когда любые s столбцов матрицы 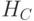 линейного кода
линейного кода 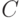 линейно независимы.
линейно независимы.
Если любые  столбцов матрицы
столбцов матрицы 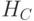 линейно независимы, то никакой вектор
линейно независимы, то никакой вектор 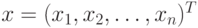 , имеющий
, имеющий  или менее ненулевых (единичных) компонент, не обращает в ноль произведение
или менее ненулевых (единичных) компонент, не обращает в ноль произведение 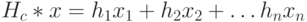 . Это означает, что нормы всех кодовых слов, то есть слов
. Это означает, что нормы всех кодовых слов, то есть слов  , для которых справедливо
, для которых справедливо 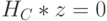 , больше
, больше  , и следовательно, кодовое расстояние
, и следовательно, кодовое расстояние 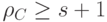 .
.
Пусть теперь линейный код 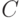 с проверочной матрицей
с проверочной матрицей 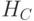 имеет кодовое расстояние
имеет кодовое расстояние 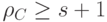 . Для доказательства линейной независимости любых
. Для доказательства линейной независимости любых  столбцов проверочной матрицы
столбцов проверочной матрицы 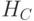 предположим противное, то есть предположим, что существует
предположим противное, то есть предположим, что существует 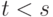 линейно зависимых столбцов матрицы
линейно зависимых столбцов матрицы 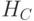 Это значит, что сумма
Это значит, что сумма 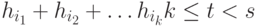 некоторых из этих столбцов равна нулевому вектору пространства
некоторых из этих столбцов равна нулевому вектору пространства  . Эту сумму можно представить как произведение
. Эту сумму можно представить как произведение 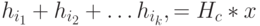 , где
, где  - вектор, у которого компоненты с номерами
- вектор, у которого компоненты с номерами 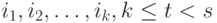 равны 1, а остальные компоненты равны 0. Значит
равны 1, а остальные компоненты равны 0. Значит  - кодовый вектор с нормой
- кодовый вектор с нормой 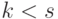 , что противоречит тому, что кодовое расстояние
, что противоречит тому, что кодовое расстояние 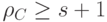 .
.
Рассмотрим некоторые примеры линейных кодов.
Код с разрядом для проверки на четность является линейным кодом с проверочной матрицей 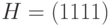 . Действительно, уравнение
. Действительно, уравнение 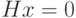 в этом случае имеет вид
в этом случае имеет вид

или

то есть четвертый разряд (проверочный), равный сумме трех информационных, делает сумму всех разрядов кодового слова четной. Каждый столбец проверочной матрицы линейно независим, поэтому из доказанной выше леммы следует, что код имеет кодовое расстояние, равное 2, и следовательно, обнаруживает одну ошибку. Ошибка обнаруживается, если число единичных разрядов в принятом слове нечетно (сумма всех разрядов принятого слова по модулю 2 не равна 0). В этом коде 8 кодовых слов.
Код с повторением является линейным кодом с проверочной матрицей
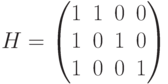
Линейное уравнение, определяющее код, в данном случае имеет вид
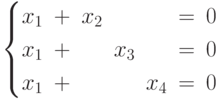
а его решения описываются соотношениями  . Эти равенства означают, что три проверочных разряда повторяют один информационный разряд. Любые 3 столбца проверочной матрицы являются линейно независимыми (сумма любых трех столбцов не равна нулевому столбцу), поэтому кодовое расстояние, равное 4, обеспечивает исправление одной ошибки и обнаружение трех. Код содержит всего 2 кодовых слова:
. Эти равенства означают, что три проверочных разряда повторяют один информационный разряд. Любые 3 столбца проверочной матрицы являются линейно независимыми (сумма любых трех столбцов не равна нулевому столбцу), поэтому кодовое расстояние, равное 4, обеспечивает исправление одной ошибки и обнаружение трех. Код содержит всего 2 кодовых слова: 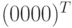 и
и 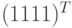 . Считается, что слово передано с ошибкой, если не все разряды в нем одинаковы. Исправление одной ошибки производится по принципу голосования. Если в полученном слове больше единичных разрядов, то, очевидно, оно ближе к кодовому слову
. Считается, что слово передано с ошибкой, если не все разряды в нем одинаковы. Исправление одной ошибки производится по принципу голосования. Если в полученном слове больше единичных разрядов, то, очевидно, оно ближе к кодовому слову 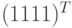 , чем к кодовому слову
, чем к кодовому слову 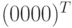 , поэтому декодирование производится в слово
, поэтому декодирование производится в слово 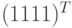 . По аналогичной причине, когда в принятом слове больше нулевых разрядов, декодирование производится в слово
. По аналогичной причине, когда в принятом слове больше нулевых разрядов, декодирование производится в слово 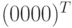 .
.