НОУ ИНТУИТ | Основы информационных технологий. Лекция 7: Передача информации

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Национальный исследовательский университет "Высшая Школа Экономики"

Опубликован: 19.11.2012 | Доступ: свободный | Студентов: 12655 / 7824 | Длительность: 29:54:00

Темы: Программное обеспечение, Образование

Специальности: Менеджер, Преподаватель

Теги: образование, офисные приложения, программное обеспечение

|

Вам нравится? Нравится 127 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Расстояние Хеминга и корректирующие возможности кодов

Определение. Код обнаруживает ошибок, если $\forall \; r \le t\; r$ ошибок в кодовом слове переводит его в слово, которое не входит в код.

Код "Тетраэдр" из предыдущего примера обнаруживает одну ошибку (меняется четность), но не обнаруживает две ошибки. Например, слово 101 в результате двух ошибок в первых двух знаках переходит в другое кодовое слово (реализуется третий вариант передачи на рис.7.7). Легко заметить, что данный код обнаруживает 3 ошибки, 5 ошибок и вообще любое нечетное число ошибок, но не обнаруживает любое четное число ошибок. Поэтому, в соответствии с приведенным определением, этот код не обнаруживает 3 или 5 ошибок, а только одну.

В пространстве B^n вводится мера отличия двух точек этого пространства, которая называется расстоянием Хеминга [29], [33], [34].

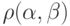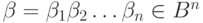Определение. Расстоянием $\rho(\alpha, \beta)$ , по Хемингу, между вершинами $\alpha=\alpha_1\alpha_2 \dots \alpha_n \in B^n$ и $\beta=\beta_1 \beta_2 \dots \beta_n \in B^n$ называется число разрядов, в которых эти вершины различаются.

В виде математической формулы это можно записывать так:

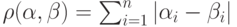
$\rho(\alpha, \beta)=\sum_{i=1}^{n}|\alpha_i-\beta_i|$

где через 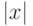|x| обозначается абсолютная величина числа .

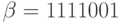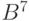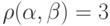В качестве примера рассмотрим расстояние Хеминга между двумя точками (последовательностями или словами) $\alpha=0110101$ и $\beta=1111001$ пространства B^7 . Эти последовательности отличаются в первой, четвертой и пятой позициях, следовательно, $\rho(\alpha, \beta)=3$ .

Вещественную функцию 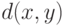d(x,y) двух переменных на множестве 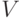принято называть расстоянием, если она обладает следующими свойствами:

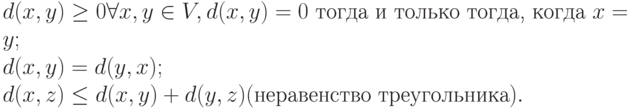
$d(x,y) \ge 0 \forall x, y \in V, d(x,y) =0 \mbox{\ тогда\ и\ только\ тогда,\ когда\ } x=y;\\ d(x,y) = d(y,x);\\ d(x,z) \le d(x,y) + d(y,z) (\mbox{неравенство треугольника}).$

Расстояние Хеминга обладает перечисленными выше свойствами. Два первых свойства очевидным образом следуют из определения расстояния Хеминга (или из приведенной выше формулы для расстояния Хеминга), а третье свойство вытекает из следующей последовательности равенств и неравенств

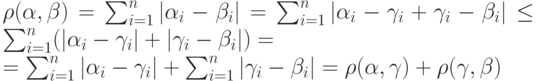
$\rho(\alpha, \beta)=\sum_{i=1}^{n}|\alpha_i-\beta_i|=\sum_{i=1}^{n}|\alpha_i-\gamma_i+\gamma_i-\beta_i|\le \sum_{i=1}^{n}(|\alpha_i-\gamma_i|+|\gamma_i-\beta_i|)=\\ =\sum_{i=1}^{n}|\alpha_i-\gamma_i|+\sum_{i=1}^{n}|\gamma_i-\beta_i|=\rho(\alpha, \gamma)+\rho(\gamma, \beta)$

Возможности обнаруживать и исправлять ошибки с помощью кода C зависят от его характеристики, которая называется кодовым расстоянием [34].

Определение. Кодовым расстоянием 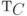т_C кода 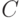называется минимальное расстояние между различными кодовыми словами (векторами).

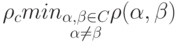
$\rho_c min_{\substack{\alpha, \beta \in C\\ \alpha \ne \beta}}\rho(\alpha, \beta)$

С использованием расстояния Хеминга в пространстве B^n можно определить аналоги таких геометрических понятий, как сфера и шар [34]. Эти понятия потребуются в дальнейшем для объяснения принципов обнаружения и исправления ошибок с помощью кодов.

Сферой радиуса с центром в точке $\alpha$ является множество

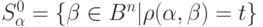
$S_{\alpha}^0=\{\beta \in B^n|\rho(\alpha, \beta)=t\}$

Число точек $|S_{\alpha}^0(t)|$ в сфере $S_{\alpha}^0(t)$ определяется выражением

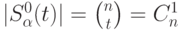
$|S_{\alpha}^0(t)|={n\choose t}=C_n^1$

Шаром радиуса с центром в точке $\alpha$ называется множество

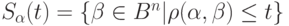
$S_{\alpha}(t)=\{\beta \in B^n|\rho (\alpha, \beta) \le t\}$

Число точек 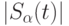$|S_{\alpha}(t)|$ в шаре 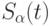$S_{\alpha}(t)$ определяется выражением

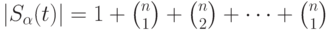
$|S_{\alpha}(t)|=1+{n\choose 1}+{n \choose 2}+\dots+{n\choose 1}$

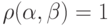Замечание. Если имеется некоторое исходное слово $\alpha$ , а слово $\beta$ получилось из $\alpha$ в результате одной ошибки, произошедшей, например, при передаче слова $\alpha$ по каналу, то $\rho(\alpha, \beta)=1$ , т. е. в смысле Хеминга расстояние между ними равно 1.

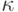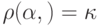Аналогичным образом, если при передаче слова $\alpha$ произошло $\kappa$ ошибок и оно превратилось в слово $\beta$ то $\rho(\alpha,\betar)=\kappa$ .

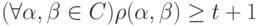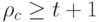Утверждение. Код обнаруживает $\tau$ ошибок, если для любых кодовых слов $\alpha$ и $\beta$ $(\forall \alpha, \beta \in C) \rho(\alpha, \beta) \ge t+1$ или $\rho_c \ge t+1$ .

Рассмотрим, как происходит декодирование сообщения после его передачи через канал. Если при передаче не произошло ошибок, то будет получено кодовое слово. Естественно считать это кодовое слово результатом декодирования.

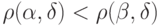Если в результате передачи получено не кодовое слово, то произошла ошибка. В этом случае целесообразно использовать декодирование в ближайшее кодовое слово. Такой подход имеет объяснение. Действительно, пусть полученное слово $\delta$ ближе к кодовому слову $\alpha$ , чем к любому другому кодовому слову, т. е. $\rho(\alpha, \delta) < \rho(\beta, \delta)$ для всех кодовых слов $b\ne a$ . Если сравнить различные гипотезы о том, какое исходное слово было пе-редано, то гипотеза о передаче слова $\alpha$ при условии получения слова $\delta$ является наиболее вероятной. Это следует из того, что первая гипотеза (основная) соответствует меньшему числу ошибок при передаче, чем конкурирующие гипотезы.

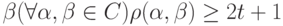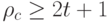Утверждение. Код исправляет ошибок, если для любых кодовых слов $\alpha$ и $\beta (\forall \alpha, \beta \in C) \rho(\alpha, \beta) \ge 2t+1$ или $\rho_c \ge 2t+1$ .

Для доказательства рассмотрим шары радиуса с центрами в кодовых словах. Из неравенства треугольника для расстояния Хеминга следует, что эти шары не пересекаются. Тогда при передаче любого кодового слова и при числе ошибок, не превышающем , полученное слово будет находиться в шаре с центром в передаваемом слове и декодироваться (по методу декодирования в ближайшее кодовое слово) в переданное слово.

Из последних двух утверждений следует, что важнейшей характеристикой кода, определяющей его корректирующие возможности, является его кодовое расстояние.

Рассмотрим, следуя [34], какие задачи требуется решать при создании кодов, с помощью которых можно эффективно обнаруживать и исправлять ошибки, возникающие при передаче сообщений. Одна из важнейших задач теории кодирования состоит в следующем. Требуется построить код, исправляющий ошибок и имеющий максимально возможное число точек. В геометрической постановке эта же задача звучит следующим образом: среди вершин единичного -мерного куба B^n требуется выделить максимальное число таким способом, чтобы расстояние между любыми двумя выделенными вершинами было не меньше, чем 2t +1 . 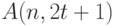Это максимальное число обозначается обычно через A(n, 2t+1) .

Другая, связанная с предыдущей, задача состоит в расположении точек в вершинах B^n так, чтобы наименьшее из попарных расстояний между ними было возможно большим. Это расстояние обозначается через d(s, n) .

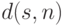Выражения "построить", "выделить", "расположить" нуждаются в уточнении, так как нам вовсе не безразлично, в каком виде будет задан искомый код. Самый простой способ - перечисление всех кодовых точек - является неэффективным, требует большой памяти. Поэтому нужен такой способ задания кода, который позволяет просто восстановить каждую точку кода по ее номеру. Другими словами, код должен иметь простую реализацию. С некоторыми просто реализуемыми кодами мы познакомимся ниже. С другой стороны, мы хотим иметь возможность просто восстанавливать исходное сообщение на выходе.

Таким образом, "хороший код" должен удовлетворять следующим трем естественным требованиям:

исправлять много ошибок, т. е. иметь большое кодовое расстояние;
иметь несложную реализацию;
обладать простым алгоритмом исправления ошибок на приемном конце.

Следует отметить, что эти требования в значительной степени являются противоречивыми, так как код , исправляющий много ошибок, вовсе не обязан иметь простую реализацию и тем более простой алгоритм декодирования. Поэтому на практике применяются коды, которые обладают в достаточной мере всеми тремя перечисленными выше качествами.

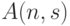A(n,s) - максимальное число точек кода в B^n , расстояние между любыми двумя кодовыми словами не меньше .

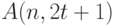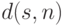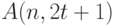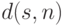Для количественной оценки свойств кода полезно знать, насколько его параметры отличаются от параметров "идеального" кода. Для этого необходимо иметь хотя бы приближенные значения важнейших параметров "идеального" кода, т. е. значения A(n, 2t+1) и d(s, n) . Следует отметить, что функции и d(s, n) не являются единственными параметрами, характеризующими качество кода. Не менее важными являются также такие параметры кода, как вероятность правильного декодирования и вероятность обнаружения ошибки. Имеется также еще ряд других важных критериев, применяющихся для оценки качества кодов.

Оценки верхних границ корректирующих способностей кодов

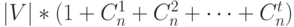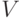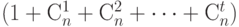Если расстояние между любыми двумя точками кода не меньше, чем 2t+1 , то шары радиуса с центрами в кодовых словах не пересекаются. Поэтому общее число точек в этих шарах равно: $|V|*(1+C_n^1+C_n^2+\dots+C_n^t)$ , где |V| - число точек (кодовых слов) в коде , а $(1 + С_n^1 + С_n^2 +\dots + С_n^t)$ число точек в шаре радиуса . 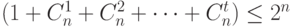Так как число точек, попавших в шары, очевидно, не превосходит общего числа точек (двоичных слов) в B^n , то $\V\*(1+C_n^1+C_n^2+\dots+C_n^t)\le 2^n$ . 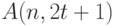Это неравенство справедливо для любого множества с расстоянием между любыми двумя точками не меньше, чем 2t+1 , в том числе и для кода с максимальным числом слов A(n, 2t+1) , откуда и следует неравенство Хеминга.

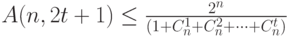
$A(n,2t+1) \le \frac{2^n}{(1+C_n^1+C_n^2+\dots+C_n^t)}$

Для максимального числа слов 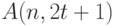A(n, 2t+1) в коде, исправляющем ошибок, может быть получена оценка снизу.

Утверждение (неравенство Варшамова - Гилберта):

$\frac{2^n}{(1+C_n^1+C_n^2+\dots+C_n^{2t})}\le A(n,2t+1)$

Чтобы доказать неравенство Варшамова - Гилберта, можно рассмотреть следующую процедуру построения кода, исправляющего ошибок.

В качестве первого кодового слова возьмем произвольное слово (вектор) из B^n . Рассмотрим шар радиуса 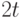с центром в данном слове. Если в B^n есть слова, не вошедшие в этот шар, то в качестве второго кодового слова выберем любое из них. В качестве третьего кодового слова выберем любое слово, не вошедшее ни в один из построенных ранее шаров. Построим шар радиуса 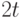с центром в данном слове. Продолжим эту процедуру выбора кодовых слов и построения шаров до тех пор, пока не будут исчерпаны все точки пространства B^n . Предположим, построение кода завершилось за шагов. 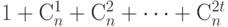После завершения этой процедуры пространство B^n будет покрыто построенными шарами, содержащими по $1+С_n^1+С_n^2+\dots+С_n^{2t}$ точек каждый. Поскольку шары могут пересекаться, справедливо неравенство 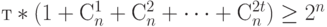$т*(1+С_n^1 + С_n^2 +\dots+С_n^{2t}) \ge 2^n$ . Центры шаров образуют код 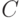, имеющий, как следует из способа построения, кодовое расстояние 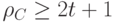$\rho_C \ge 2t+1$ . Из того, что 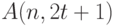A(n, 2t +1) - это максимально возможное число точек кода с кодовым расстоянием не меньше, чем 2t+1 , следует, что $A(n, 2t+1)\ge m$ и $А(п, 2t+1)*(1+С_n^1+С_n^2+\dots+С_n^{2t})\ge 2^n$ . Последнее неравенство эквивалентно неравенству Варшамова - Гилберта.

Дальше >>

Авторизоваться

Основы информационных технологий

Передача информации

Расстояние Хеминга и корректирующие возможности кодов

Оценки верхних границ корректирующих способностей кодов

Вопросы и ответы