|
Символы кириллицы выводит некорректно. Как сделать чтобы выводился читабельный текст на русском языке? Тип приложения - не Qt, Qt Creator 4.5.0 основан на Qt 5.10.0. Win7.
|
Статические и динамические матрицы
Задача 6.12. Найти определитель квадратной матрицы 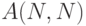 .
.
Пусть задана матрица (6.2), необходимо вычислить её определитель. Для этого матрицу необходимо преобразовать к треугольному виду (6.3), а затем воспользоваться свойством, известным из курса линейной алгебры, которое гласит, что определитель треугольной матрицы равен произведению её диагональных элементов: 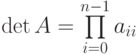 .
.
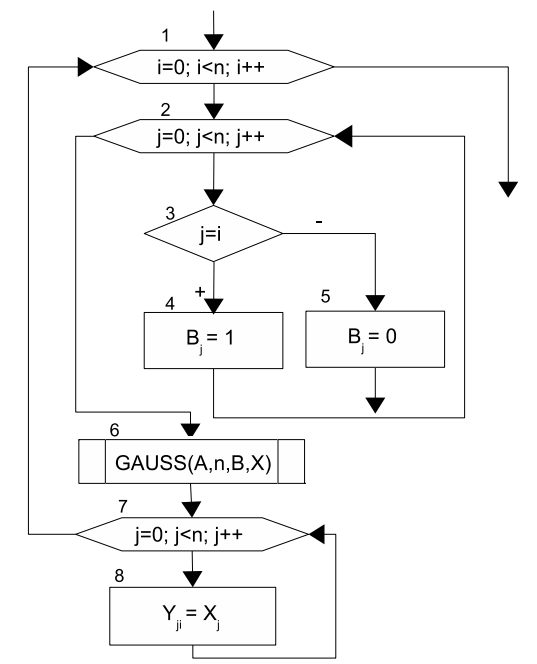
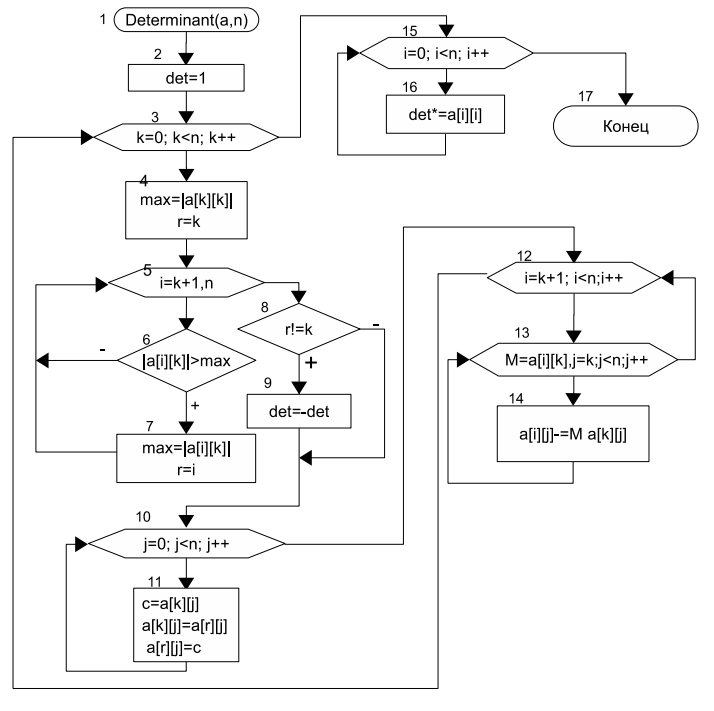
Преобразование матрицы (6.2) к виду (6.3) можно осуществить с помощью прямого хода метода Гаусса. Алгоритм вычисления определителя матрицы, изображённый в виде блок-схемы на рис. 6.16, представляет собой алгоритм прямого хода метода Гаусса, в процессе выполнения которого проводится перестановка строк матрицы. Эта операция приводит к смене знака определителя. В блок- схеме момент смены знака отражён в блоках 8–9. В блоке 8 определяется, будут ли строки меняться местами, и если ответ утвердительный, то в блоке 9 происходит смена знака определителя. В блоках 15–16 выполняется непосредственное вычисление определителя путём перемножения диагональных элементов преобразованной матрицы.
На листинге приведён текст программы решения задачи 6.12 с комментариями.
#include <iostream>
#include <math.h>
using namespace std;
//Функция вычисления определителя.
double determinant ( double ** matrica_a, int n )
//Формальные параметры: matrica_a — исходная матрица, n — размер матрицы,
//функция возвращает значение определителя (тип double.)
{
int i, j, k, r;
double c,M, max, s, det =1;
//a — копия исходной матрицы.
double **a;
//Выделение памяти для матрицы a .
a=new double * [ n ];
for ( i =0; i<n; i++)
a [ i ]=new double [ n ];
//В a записываем копию исходной матрицы.
for ( i =0; i<n; i++)
for ( j =0; j<n; j++)
a [ i ] [ j ]=matrica_a [ i ] [ j ];
//Прямой ход метода Гаусса.
for ( k=0;k<n; k++)
{
max=fabs ( a [ k ] [ k ] );
r=k;
for ( i=k+1; i<n; i++)
if ( fabs ( a [ i ] [ k ] )>max)
{
max=fabs ( a [ i ] [ k ] );
r= i;
}
//Если строки менялись местами, то смена знака определителя.
if ( r !=k ) det=-det;
for ( j =0; j<n; j++)
{
c=a [ k ] [ j ];
a [ k ] [ j ]=a [ r ] [ j ];
a [ r ] [ j ]= c;
}
for ( i=k+1; i<n; i++)
for (M=a [ i ] [ k ] / a [ k ] [ k ], j=k; j<n; j++)
a [ i ] [ j ]-=M*a [ k ] [ j ];
}
//Вычисление определителя.
for ( i =0; i<n; i++)
det*=a [ i ] [ i ];
//Возврат определителя в качестве результата функции
for ( i =0; i<n; i++)
delete [ ] a [ i ];
delete [ ] a;
return det;
}
int main ( )
{
int result, i, j,N;
double **a, b;
cout<<" N = ";
cin>>N;
a=new double _ [N ];
for ( i =0; i<N; i++)
a [ i ]=new double [N ];
//Ввод значений исходной матрицы.
cout<<"Ввод матрицы A "<<endl;
for ( i =0; i<N; i++)
for ( j =0; j<N; j++)
cin>>a [ i ] [ j ];
//Обращение к функции вычисления определителя.
cout<<"определитель= "<<determinant ( a,N)<<endl;
}В этой главе читатель познакомился с обработкой статических и динамических матриц в C++, а также с использованием функций для решения задач обработки динамических матриц.