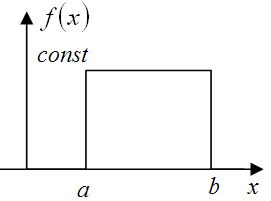НОУ ИНТУИТ | Основы теории вероятностей. Лекция 5: Функция распределения случайной величины. Виды распределения

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 28.04.2012 | Доступ: свободный | Студентов: 3114 / 894 | Оценка: 3.86 / 2.57 | Длительность: 07:45:00

Тема: Математика

Теги: beta, анализ, биноминальное распределение, бифуркация, вычисления, графика, дискретная случайная величина, законы, несовместное событие, нормальная функция, ось ординат, полная группа, распределение пуассона, формула полной вероятности, цвета, элементарное события

|

Вам нравится? Нравится 32 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Свойства функции плотности распределения f(x)

Для непрерывной случайной величины можно определить не только функцию распределения, которая является интегральной характеристикой случайной величины, но и дифференциальную функцию. Такая функция называется плотностью распределе-ния или дифференциальным законом распределения случайной величины.

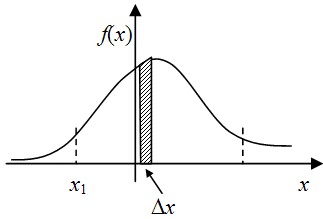
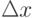Для определения функции плотности распределения разобьем весь интервал $[x_{1},x_{n}]$ на элементарные отрезки $\Delta x$ . Тогда вероятность попадания случайной величины $X$ в этот интервал будет (по свойству 2) равно

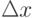
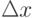$P(x \leqslant X \leqslant x+\Delta x)= F(x+\Delta x)-F(x)$

Разделим последнее выражение на $\Delta x$

$\frac {P(x \leqslant X \leqslant x+\Delta x)} {\Delta x } =\frac { F(x+\Delta x)-F(x) } {\Delta x }$

и будем уменьшать $\Delta x$ до нуля. Тогда, переходя к пределу, получим

$\lim\limits_{\Delta x \to 0} \frac {P(x \leqslant X \leqslant x+\Delta x)} {\Delta x } =\lim\limits_{\Delta x \to 0} =\frac { F(x+\Delta x)-F(x) } {\Delta x }=F'(x)=f(x)$

( 4)

Рис. 9.4. Функция плотности распределения вероятностей

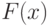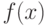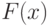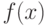Кривая функции плотности распределения (4) будет иметь вид, представленный на рис.9.4 . Очевидно, что $F(x)$ будет являться первообразной функции $f(x)$ , т.е. используя определение интеграла, можно установить математическую зависимость между $F(x)$ и $f(x)$ , т.е. по определению интеграла

$F(x)=\int\limits_{a}^{b}f(x)dx=S$

функция распределения $F(x)$

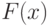численно равна площади под кривой $f(x)$

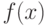на интервале $[a;b)$

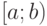. Тогда, на основании свойства 4 функции распределения, можно записать

$\int\limits_{-\infty}^{+\infty}f(x)dx=1$

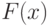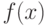Определение. Случайная величина $X$ называется непрерывной, если ее функция распределения $F(x)$ представлена непрерывной функцией для любой точки из области $(-\infty;+infty)$ , а функция плотности распределения $f(x)$ существует везде, за исключением, может быть, конечного числа точек.

Вследствие равенства (4) из свойств функции распределения 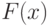$F(x)$ вытекают свойства функции плотности распределения $f(x)$ .

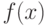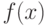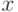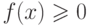Свойство 1. Дифференциальная функция распределения $f(x)$ не отрицательна для любого $x$ из ее области определения $f(x) \geqslant 0$ .

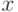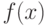Свойство 2. Вероятность попадания непрерывной случайной величины $x$ в интервал $[\alpha;\beta]$ равен определенному интегралу от функции плотности распределения $f(x)$ на этом интервале

$P(\alpha \leqslant x \leqslant \beta) =\int\limits_{\alpha}^{\beta}f(x)dx$

( 5)

Свойство 3. Интегральная функция распределения случайной величины может быть выражена через функцию плотности вероятностей по формуле

$F(x)=\int\limits_{-\infty}^{x}f(x)dx$

( 6)

Свойство 4. Площадь под кривой плотности распределения на всей ее области определения равен единице

$\int\limits_{-\infty}^{+\infty}f(x)dx=1$

( 7)

Свойство 5. Математическое ожидание непрерывной случайной величины вычисляется по формуле

$M_{X}=p(x) \cdot x=\int\limits_{a}^{b}xf(x)dx$

( 8)

Свойство 6. Дисперсия непрерывной случайной величины вычисляется по формуле

$D_{X}=\int\limits_{a}^{b}\left (x-M_{X} \right)^2 f(x)dx$

( 9)

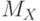где $M_{X}$ вычисляется по формуле (8).

Равномерное распределение

Непрерывная случайная величина имеет равномерное распределение на и полуинтервале 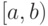$[a,b)$ , если на этом интервале плотность распределения случайной величины (рис.9.6 ) постоянна, а вне этого интервала равна нулю, т.е.

$f(x)=\left\{\begin{array}{ccc}{0, \ \ \ \ \ \ x<a;}\\{ const, a\leqslant x<b;}\\{0, b\leqslant x}\\\end{array}\right}$

( 10)

Рис. 9.6. Функция плотности распределения вероятностей

Такое распределение случайной величины еще называют законом равномерной плотности. Найдем величину 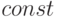$const$ , пользуясь свойством 4 функции плотности распределения и формулами (7) и (10):

$\int\limits_{-\infty}^{+\infty}f(x)dx= \int\limits_{-\infty}^{a}f(x)dx+\int\limits_{a}^{b}f(x)dx+\int\limits_{b}^{+\infty}f(x)dx =\int\limits_{-\infty}^{a}0\,dx+\int\limits_{a}^{b}const\,dx+\int\limits_{b}^{+\infty}0\,dx =\int\limits_{a}^{b}const\,dx =1$

откуда получаем

$\int\limits_a^b const \cdot dx =1 \Rightarrow const=\frac 1{b-a}$

( 11)

Таким образом, формула (10) с учетом результата (11) запишется в виде

$f(x)=\left\{\begin{array}{ccc}{0, \ \ \ \ \ \ x<a;}\\{\frac1 {b-a}, a\leqslant x<b;}\\{0, b\leqslant x}\\\end{array}\right}$

( 12)

Тогда функция распределения по (6) с учетом (12) имеет вид

$F(x)= \int\limits_{-\infty}^{x}f(x)dx = \int\limits_{a}^{x}\frac {1} {b-a}dx =\frac {x} {b-a}\left |_a^x=\frac {x-a}{b-a},$

( 13)

т.е.

$F(x)=\left\{\begin{array}{ccc}{0, \ \ \ \ \ \ x<a;}\\{\frac{x-a} {b-a}, a\leqslant x<b;}\\{0, b\leqslant x}\\\end{array}\right}$

( 14)

График функции (14) изображен на рис.9.7 .

Рис. 9.7. Функция распределения зависимости

Определим теперь математическое ожидание на основании свойства 5 и формул (8) и (12) для равномерного распределения. Получим

$M_{X}= \int\limits_{a}^{b}xf(x)dx = int\limits_{a}^{b}\frac {x} {b-a}dx =\frac {x^2} {2(b-a)}\ left |_a^b=\frac {a+b} 2.$

( 15)

Свойство математического ожидания, выраженное формулой (15) является признаком, по которому можно установить, что данные экспериментального ряда распределены по равномерному закону. Это можно использовать и для дискретного ряда.

Пример 2. Определить тип распределения для вариационного ряда 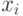$x_{i}$ $m_{i}$

Таблица возможных исходов
Xi	1	2	3	4	5	6
Mi	3	2	6	7	5	2

Решение. Найдем математическое ожидание ряда по обычной формуле

$M_{X}=\frac {1 \cdot 3+2 \cdot 2+ 3 \cdot 6 + 4 \cdot 7 +5 \cdot 2 + 6 \cdot 5} {25}=3,72$

и вычислим по формуле (15)

$M_{X}=\frac {1+6} 2=3,5$

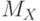Сравнивая результаты, получаем, что оба значения $M_{X}$ различаются между собой меньше, чем на 10 %, поэтому заключаем, что данный вариационный ряд, скорее всего, подчиняется равномерному закону.

Определим остальные статистические характеристики распределения.

$D_{X}=\mu_{2}X=\int\limits_{a}^{b} \left ( x-\frac {b+a} 2\right )^2 \cdot \frac 1 {b-a} dx=\frac {(b-a)^2} {12};$

( 16)

$\sigma=\sqrt {D_{X}} =\frac {b-a} {2\sqrt 3} ;$

( 17)

$A=\frac {\mu^3} {\sigma^3} =0,$

( 18)

так как распределение симметрично относительно своего среднего значения

$\mu_{4}=\int\limits_{a}^{b} \left ( x-\frac {b+a} 2\right )^4 \cdot \frac 1 {b-a} dx=\frac {(b-a)^4} {80};$

( 19)

$E=\frac {\mu^4} {\sigma^4}-3 =-1,2.$

( 20)

Характеристики (16) – (20) равномерного распределения можно использовать всякий раз, когда по (15) установлено, что данный экспериментальный ряд подчиняется равномерному закону распределения.

Дальше >>

Авторизоваться

Основы теории вероятностей

Функция распределения случайной величины. Виды распределения

Свойства функции плотности распределения f(x)

Равномерное распределение

Вопросы и ответы