Функция распределения случайной величины. Виды распределения
Функция распределения
Известно, что если события составляют полную совокупность, то  . Тогда совокупность всех возможных значений случайной величины и соответствующих им вероятностей составляет распределение случайной величины.
. Тогда совокупность всех возможных значений случайной величины и соответствующих им вероятностей составляет распределение случайной величины.
Определение. Законом распределения или функций распределения случайной величины называется всякое соответствие между всевозможными значениями случайной величины и соответствующим им вариантом.
Определение. Случайные величины называются независимыми, если закон распределения одной не зависит от закона распределения другой.
В противном случае величины будут зависимыми.
Для дискретной случайной величины, которая может принимать значения 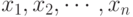 _ функция распределения имеет вид:
_ функция распределения имеет вид:
![\[F \left ( X \right )=\sum\limits_{x_{i}<x} \left ( X < x_{i}\right )]](/sites/default/files/tex_cache/925d78fd204257336d429f8ac1a9fbc1.png) |
( 1) |
Выражение (1) читается так: "функция распределения численно равна вероятности того, что случайная величина  примет значение не больше, чем
примет значение не больше, чем 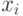 ".
".
Пусть теперь некоторая случайная величина примет значения из ряда 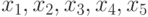 с вероятностями
с вероятностями 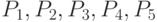 , соответственно. Тогда очевидно, что вероятность того, что значение случайной величины
, соответственно. Тогда очевидно, что вероятность того, что значение случайной величины  будет меньше
будет меньше 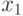 равно 0:
равно 0: 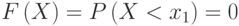 , а вероятность того, что
, а вероятность того, что  будет меньше
будет меньше 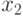 , равна
, равна 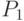 :
: 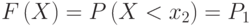 . Вероятность, что случайная величина
. Вероятность, что случайная величина  будет меньше
будет меньше 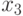 будет равна
будет равна 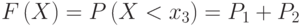 , так как
, так как 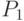 - это вероятность варианты
- это вероятность варианты 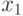 , а
, а 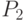 - вероятность варианты
- вероятность варианты 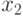 . Случайная величина принимает одно значение из двух
. Случайная величина принимает одно значение из двух 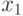 либо
либо 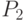 , потому
, потому  . Но тогда, рассуждая аналогично, получаем:
. Но тогда, рассуждая аналогично, получаем:
![\[ F\left ( X \right )=P\left ( X <x_{4} \right )=P_{1}+P_{2}+P_{3} \]](/sites/default/files/tex_cache/de56f394ec7cb0be2e65387eb1f8ccc4.png)
![\[ F\left ( X \right )=P\left ( X <x_{5} \right )=P_{1}+P_{2}+P_{3}+P_{4} \]](/sites/default/files/tex_cache/980c1c1837a361e519c940e9af31cde3.png)
![\[ F\left ( X \right )=P\left ( X <x_{6} \right )=P_{1}+P_{2}+P_{3}+P_{4}+P_{5}=1 \]](/sites/default/files/tex_cache/583b0041769a5e3b8323ba5b0da5849e.png)
Последнее выражение равно 1, так как все пять событий образуют полную группу. Здесь 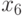 любое число, которое просто больше
любое число, которое просто больше 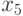 ,
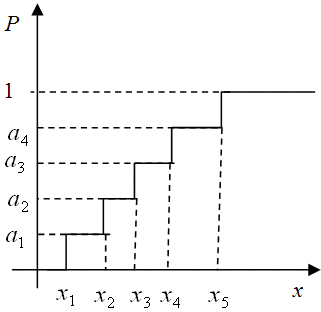
,  . Сказанное можно изобразить графически ( рис.9.1 ), если по оси ординат откладывать вероятности
. Сказанное можно изобразить графически ( рис.9.1 ), если по оси ординат откладывать вероятности 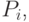 по оси абсцисс – сами значения случайной величины.
по оси абсцисс – сами значения случайной величины.
Очевидно, что
![\[ a_{1}=p_{1}; \ a_{2}-a_{1}=p_{2};\]](/sites/default/files/tex_cache/4d879cac15f4091a1dd2660542048e95.png)
![\[ a_{3}-a_{2}=p_{3}; \ a_{4}-a_{3}=p_{4};\]](/sites/default/files/tex_cache/004cf08dbfedd35bfe05cc9306a3a0f2.png)
![\[ 1-a_{4}=p_{5}.\]](/sites/default/files/tex_cache/73a40637c69e741c76a0c526ea67ecc7.png)
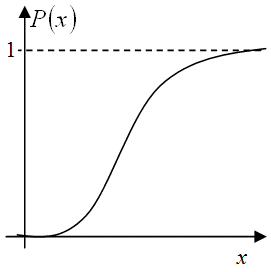
Если бы наша случайная величина была бы непрерывной, то тогда распределенное 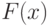 выглядела несколько бы иначе ( рис.9.2 ).
выглядела несколько бы иначе ( рис.9.2 ).
Свойства функции F(x)
Функции распределения для дискретной и непрерывной величин обладают рядом одинаковых очевидных свойств, в вытекающих из ее определения.
Свойство 1. Функция распределения есть не отрицательная функция, значение которой изменяются от 0 до 1:
![\[0\leqslant F(x) \leqslant 1\]](/sites/default/files/tex_cache/d89da9b8ef52ea6a88964412dcb3c5f8.png) |
( 2) |
Свойство 2. Вероятность попадания случайной величины в некоторый интервал ![$[a,b]$](/sites/default/files/tex_cache/fe477a2781d275b4481790690fccd15f.png) равно разности значений функций распределений на концах этого интервала
равно разности значений функций распределений на концах этого интервала
![\[ P(a \leqslant x <b)=F(b)-F(a) \]](/sites/default/files/tex_cache/177cb603403853afeee3c58f860558fb.png) |
( 3) |
Следствие. Вероятность попадания непрерывной случайной величины в не конкретный интервал равна нулю.
Свойство 3. Функция распределения случайной величиной есть не убы-вающая функция, т. е. при  имеем
имеем
![\[F(\beta)-F(\alpha) \geqslant 0 \]](/sites/default/files/tex_cache/ca8b586fc9d44e8f6c6afa02e5bc83ca.png)
![\[ F(\beta) \geqslant F(\alpha) \]](/sites/default/files/tex_cache/265758774c17548bd6898e038fd282f3.png)
Свойство 4. Значение функции распределения на  равно нулю, и единице ? на
равно нулю, и единице ? на  , т.е.
, т.е.
![\[ F(-\infty)=0; \ F(+\infty)=1 \]](/sites/default/files/tex_cache/a61348d6d861891cdd3dd028f808eb67.png)
Пример 1. Построить функцию распределения вариационного ряда 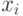

Решение. Найдем вероятности вариант. Если  , то имеем
, то имеем
![\[ P_{1}=\frac 3 {25}; \ P_{2}=\frac 2 {25}; \ P_{3}=\frac 6 {25}; \ P_{4}=\frac 7 {25}; \ P_{5}=\frac 2 {25}; \ P_{6}=\frac 5 {25}.\]](/sites/default/files/tex_cache/6f94869cce1fecc56655db301f16eff2.png)
![\[ F(x)=\left\{\begin{array}{ccccccc}{0, \ \ \ \ \ \ x<1}\\{\frac 3 {25},1\leqslant x<2}\\{\frac 5 {25},2\leqslant x<3}\\{\frac {11} {25},3\leqslant x<4}\\{\frac {18} {25},4\leqslant x<5}\\{\frac {20} {25},5\leqslant x<6}\\{1,6\leqslant x}\\ \end{array}\right} \]](/sites/default/files/tex_cache/560c9d8bc94056a1e86e13390d53cbc3.png) |
( 4) |