Основы теории вероятностей
[+]
Опубликован: 28.04.2012 | Доступ: свободный | Студентов: 3115 / 894 | Оценка: 3.86 / 2.57 | Длительность: 07:45:00
Тема: Математика
Специальности: Математик, Преподаватель
Теги: beta, анализ, биноминальное распределение, бифуркация, вычисления, графика, дискретная случайная величина, законы, несовместное событие, нормальная функция, ось ординат, полная группа, распределение пуассона, формула полной вероятности, цвета, элементарное события
Практическая работа 4:

Случайные величины. Законы распределения. Числовые характеристики случайных величин
A
|
версия для печати
< Лекция 4 || Практическая работа 4: 12 || Лекция 5 >

Пример 5. Построить ряд и начертить полигон частот для следующего распределения некоторой величины. Результаты измерений приведены в процентах.

39 41 40 42 41 40 42 44 43 42 41 43
39 42 41 42 39 41 37 43 41 38 43 42
41 40 41 38 44 40 42 40 41 42 40 43
38 39 41 41 42

Перейти к интервальному ряду. Построить гистограмму частот.

Решение. Для построения статистического (вариационного) ряда значения признака (результаты измерений) располагаем в порядке возрастания, предполагая, что данные независимы. Длина ряда $n=41$

37 38 38 38 39 39 39 39 40 40 40 40
40 40 41 41 41 41 41 41 41 41 41 41
41 42 42 42 42 42 42 42 42 42 43 43
43 43 43 44 44
Полигон частот для примера 5

Рис. 8.1. Полигон частот для примера 5

И затем подсчитаем для каждого значения частоту его появления

x 37 38 39 40 41 42 43 44
m 1 3 4 6 11 9 5 2

Теперь построим полигон частот, откладывая по оси абсцисс значения 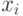$x_{i}$, а по оси ординат - $m_{i}$. Полигон изображен на рис. 8.1.

Для того чтобы перейти к интервальному ряду, воспользуемся формулой (2): $h=\frac {44-37} {log_{2}41 +1}=\frac {7} {6,48} \approx 1,1$. Определим нижнюю границу интервального ряда: $a=x_{min}-\frac h 2 \approx 36,45$ и составим интервальный ряд:

N 1 2 3 4 5 6 7
( X_i;X_i+1 ) (36,45; 37,55) (37,55; 38,65) (38,65; 39,75) (39,75; 40,85) (40,85; 41,95) (41,95; 43,05) (43,05; 44,15)
m_i 1 3 4 6 11 14 2
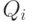Q_i 1/41 3/41 4/41 6/41 11/41 14/41 2/41
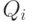Q_i 0,02 0,07 0,09 0,14 0,25 0,32 0,05

Теперь по оси абсцисс отложим значения интервалов $(x_{i};x_{i+1})$ и пронумеруем их, согласно построению. По оси ординат отложим частости $Q_{i}$. Гистограмма имеет вид, представленный на рис. 8.2. По сравнению с рис. 8.1 ее вид несколько изменился: максимум сместился вправо и левая ветвь более затянута по сравнению с полигоном частот.

Гистограмма интервального ряда примера 5

Рис. 8.2. Гистограмма интервального ряда примера 5

Пример 6. Определить основные статистические характеристики ряда, приведенного в примере 5.

Решение. Математическое ожидание находим по формуле (3):

\[ M_{X}^*=\overline x=\frac 1 {41} (37 \cdot 1 +38 \cdot 3 +39 \cdot 4 + 40 \cdot 6+41 \cdot 11 +42 \cdot 9 +43 \cdot 5 + 44 \cdot 2)= \frac {1679} {41} \approx 40,95\]
Для того чтобы подсчитать остальные статистические характеристики и моменты составим для удобства вычислений таблицу (таблица 1), которая формируется следующим образом. Столбец 3 получается как результат перемножения данных соответствующих строк первого и второго столбцов. В столбец 4 помещаются результаты вычитания из данных столбца 1 подсчитанного математического ожидания $M_{X}^*=40,95$. В столбце 5 стоят квадраты соответствующих строк столбца 4. В столбце 6 – квадраты данных столбца 1. Столбец 7 формируется путем перемножения соответствующих строк столбцов 6 и 2. Столбец 8 формируется путем перемножения соответствующих строк столбцов 5 и 2. В последней строке стоят суммы данных по столбцам. Подсчитаны только те суммы, которые будут использоваться для вычисления статистических характеристик и статистических моментов ряда.

Таблица 8.1. Вспомогательная таблица для расчета статистических характеристик ряда
$x_{i}-\overline x$ $(x_{i}-\overline x)^2$ $(x_{i})^2$ $(x_{i})^2m_{i}$ $(x_{i}-\overline x)^2m_{i}$
37 1 37 -3.95 15.61 1369 1369 15.61
38 3 114 -2.95 8.71 1444 4332 26.13
39 4 156 -1.95 3.81 1521 6084 15.23
40 6 240 -0.95 0.9 1600 9600 5.43
41 11 451 0.05 0.00 1681 18491 0.03
42 9 378 1.05 1.1 1764 15876 9.90
43 5 215 2.05 4.2 1849 9245 20.99
44 2 88 3.05 9.30 1936 3872 18.59
Сумма 41 1679 68869 111.90

Таблицы, подобные таблице 8.1, удобно составлять для упрощения вычислений, выполняемых как при помощи калькуляторов, так и при привлечении программных средств. Суммы, стоящие в столбце 3, используется в формуле (3), в столбце 7 – в формулах (3), (5), (7) и (9) при $s=2$, в столбце 8 – в формулах (4), (6), (7) и (9) также при $s=2$. Пользуясь результатами таблицы 1, вычислим требуемые статистические характеристики и моменты.

\[ D_{X}^*=\frac 1 n \sum\limits_{i=1}^n (x_{i}-\overline x)^2}=\frac {111,90} {41} \approx 2,73\]
\[ \sigma=\sqrt {D_{X}^*}=\sqrt{2,73} \approx 1,65\]
\[ \alpha_{s}^2=\frac 1 {\sum\limits_{i=1}^n m_{i}} \sum\limits_{i=1}^n x_{i}^2m_{i}=\frac {68869} {41} \approx 1679,73\]
\[ m^2=\frac 1{n-1} \sum\limits_{i=1}^n (x_{i}-\overline x)^2}=\frac {111,90} {40} \approx 2,80\]
\[ \mu_{2}^*=\frac 1 {\sum\limits_{i=1}^n m_{i}} \sum\limits_{i=1}^n (x_{i}-\overline x)^2}m_{i}\approx D_{X}^*=2,73\]
Можно самостоятельно убедиться, что результаты вычислений по формулам (8) и (5) совпадают. Аналогично совпадают результаты вычислений по формулам (9) и (6).

Пример 7. Найти выражение для $D_{X}^*$ через статистические начальные моменты.

Решение. Распишем подробно формулу (4), раскроем скобки и разделим почленно на 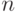$n$, получаем:

\[ D_{X}^*= \frac 1 n \sum\limits_{i=1}^n \left (x_{i}-\overline x \right )^2=\frac 1 n \sum\limits_{i=1}^n \left (x_{i}^2-2x_{i}\overline x+\overline x ^2 \right)}= \sum\limits_{i=1}^n \left (\frac {x_{i}^2} {n} + \left ( \frac {-2x_{i}\overline x} {n}\right) +\frac {\overline x^2} {n} \right)}\]
Пользуясь свойствами сложения конечных рядов и, учитывая, что \overline x является константой, получим следующее выражение
\[ D_{X}^*= \sum\limits_{i=1}^n \frac { x_{i}^2} n + \sum_{i=1}^n \frac {-2x_{i}\overline x} {n} +\sum\limits_{i=1}^n \frac {\overline x^2} {n}= \frac 1 n \sum\limits_{i=1}^n {x_{i}^2} n -\frac 2 n }\overline x \sum\limits_{i=1}^n {x_{i } +\frac 1 n \sum\limits_{i=1}^n {\overline x^2} =\frac 1 n \sum\limits_{i=1}^n {x_{i}^2} n -\frac 2 n }\overline x \sum\limits_{i=1}^n {x_{i } +\frac {\overline x^2} n \sum\limits_{i=1}^n 1 =\cdots \]
откуда с учетом (5), получаем
\[ \cdots = \alpha_{2}^*-2 \overline x \alpha_{1}^*+{\overline x^2}= \alpha_{2}^*-2 \overline x \cdot \overline x +{\overline x^2}= \alpha_{2}^*-{\overline x^2}= \alpha_{2}^*-\alpha_{1}^*\]
Т.е. искомая формула имеет довольно известный вид:
\[ D_{X}^*= \alpha_{2}^*-\alpha_{1}^*\] ( 10)
Выражение (10) дает удовлетворительные результаты и более удобно в вычислениях, так как нет необходимости вычислять разности $(x_{i}-\overline x)$

Дальше >>
< Лекция 4 || Практическая работа 4: 12 || Лекция 5 >

Вопросы и ответы

вопросов: 0