Случайная величина и ее основные характеристики.
Свойства основных характеристик случайной величины
К основным характеристикам случайной величины относятся математическое ожидание (2), среднее значение (3), мода, медиана, дисперсия (4) и среднеквадратичное отклонение(5). Рассмотрим подробнее их свойства.
Если случайная величина независимая (это всегда, если речь идет об экспериментальных данных), то можно убедиться, что формулы (2) и (3) совпадают, т.е. 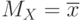 . Этот факт широко используют на практике.
. Этот факт широко используют на практике.
Свойство 1. Сумма наблюдаемых данных остается неизменной, если каждое из них заменить средним арифметическим.
Действительно, с учетом (3), получим
![\[ S=\sum\limits_{i=1}^N x_{i}= \sum\limits_{i=1}^N \overline x =\overline x \sum\limits_{i=1}^N 1=N \cdot \overline x= N \frac 1 N \sum\limits_{i=1}^N x_{i}=\sum\limits_{i=1}^N x_{i}\]](/sites/default/files/tex_cache/65541837559fba963843b19ded5b1332.png)
![\[ \overline {x}_{q}=\sqrt[q]{\frac {\sum\limits_{i=1}^N x_{i }^q} N} \]](/sites/default/files/tex_cache/2c9800db8cd743deef4e8d6bd1036a7b.png) |
( 14) |
 , то формула (14) имеет вид
, то формула (14) имеет вид![\[ \overline {x}_{\sigma}=\sqrt{\frac {\sum\limits_{i=1}^N x_{i }^2 \cdot m_{x}} {\sum m_{x}}} \]](/sites/default/files/tex_cache/b5384c3136584b1efaa3adfd87be69e5.png) |
( 15) |
Свойство 2. Средняя сумма отклонений значений ряда от среднего значения ряда равна нулю:
![\[ \sum\limits_{i=1}^N (x_{i} - \overline x) \cdot m_{x} = 0\]](/sites/default/files/tex_cache/337332fe0846dea0cacd210468f8e111.png)
Свойство 3. Среднее постоянной величины равна самой постоянной
![\[ \overline x (const) = const. \]](/sites/default/files/tex_cache/9166c6fd417c895c42fe6fcfc828d36f.png)
Свойство 4. Если от каждого значения ряда отнять (прибавить) постоянную, то среднее тоже уменьшиться (увеличится) на эту же величину:
![\[ \overline X=\frac 1 N \sum\limits_{i=1}^N x_{i}; \ =\frac 1 N \sum\limits_{i=1}^N (x_{i}+const)=\overline X +const \]](/sites/default/files/tex_cache/e9660d5e20e4090fd82d8bd805dde372.png)
Свойство 5. Если каждое значение ряда 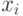 увеличить (уменьшить) в раз, где - произвольное рациональное число, то среднее ряда тоже увеличиться (уменьшиться) в такое же число раз.
Если
увеличить (уменьшить) в раз, где - произвольное рациональное число, то среднее ряда тоже увеличиться (уменьшиться) в такое же число раз.
Если 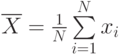 , то
, то ![$ \frac 1 N \sum\limits_{i=1}^N x_{i} ]cdot k = \overline X \cdot k$](/sites/default/files/tex_cache/6bca86bbcb98a21282c1f860a738bcd1.png)
Свойство 6. Средняя сумма двух экспериментальных рядов равна сумме средних этих рядов:
![\[\overline {x+y}=\overline x + \overline y \ или \ \overline X + \overline Y =\frac { n_{1} \overline X +n_{2} \overline Y} {n_{1}+n_{2}} ; \]](/sites/default/files/tex_cache/975bcd4370fe77692f335522bb464e8c.png)
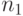 - длина первого ряда,
- длина первого ряда, 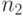 - длина второго ряда.
- длина второго ряда.Свойства показателей вариации
Одним из основных показателей ряда считается размах ряда или амплитуда:
![\[ R=x_{max}-x_{min},\]](/sites/default/files/tex_cache/c83e24d94aa56fcfa856f9fc9ef7c115.png)
Мерой рассеяния данных около среднего значения считается дисперсия 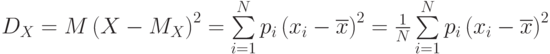
Асимметрия (10) характеризует преимущественное расположение 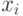 относительно среднего значения. Если
относительно среднего значения. Если 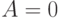 , то данные расположенные сим-метрично по отношению к . Если
, то данные расположенные сим-метрично по отношению к . Если  , то в данных преобладают значения
, то в данных преобладают значения 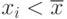 , небольшие значения, говорят, что ряд смещен влево. Если же
, небольшие значения, говорят, что ряд смещен влево. Если же 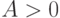 , то говорят, что ряд "смещен" вправо относительно среднего, т.е. в данных преобладают большие значения.
, то говорят, что ряд "смещен" вправо относительно среднего, т.е. в данных преобладают большие значения.
Эксцесс (11) с 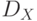 характеризует лишь расстояние данных относи-тельно среднего. Если
характеризует лишь расстояние данных относи-тельно среднего. Если  , то в данных наблюдается большая дисперсия, которая не уменьшается по мере удаления от среднего значения. Если
, то в данных наблюдается большая дисперсия, которая не уменьшается по мере удаления от среднего значения. Если  , то данные сгруппированы возле среднего, очень плотно.
, то данные сгруппированы возле среднего, очень плотно.
