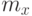Случайная величина и ее основные характеристики.
Гистограмма. Полигон частот. Непрерывное распределение
Для экспериментальной информации характерно большое количество разнообразных наблюдаемых значений, которые отличаются друг от друга на небольшую величину. В таком случае рекомендуется от дискретного распределения перейти к непрерывному ряду. Данный переход может выполняться двумя способами.
Первый способ рекомендуется для длинных рядов ( 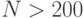 ). Этот переход основан на использовании коэффициента Стэрджеса
). Этот переход основан на использовании коэффициента Стэрджеса
![\[h=\frac { x_{max} -x_{min} } {1+3,322 \cdot lnN } \]](/sites/default/files/tex_cache/3d422d4974376d26251fe0d63fdf3c78.png) |
( 12) |
![$\left [ x_{max};x_{min} \right]$](/sites/default/files/tex_cache/92e5582976c150caa4d4fa55be8acda8.png) экспериментальных данных. В формуле (12) обозначено
экспериментальных данных. В формуле (12) обозначено 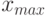 - наибольшее и
- наибольшее и 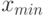 - наименьшее значения вариант исследуемого вариационного ряда;
- наименьшее значения вариант исследуемого вариационного ряда; 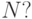 длина вариационного ряда (общее количество измерений); 3,222 -константа, определяемая из предположения, что данное распределение нормально . Весь интервал
длина вариационного ряда (общее количество измерений); 3,222 -константа, определяемая из предположения, что данное распределение нормально . Весь интервал ![$\left [ x_{max};x_{min} \right]$](/sites/default/files/tex_cache/92e5582976c150caa4d4fa55be8acda8.png) разбивают следующим образом
разбивают следующим образом![\[a_{0}= x_{min} -\frac h 2; \]](/sites/default/files/tex_cache/1746e82ed8fd1cedee3d0f132171b365.png)
![\[a_{1}= a_{0}+ h; \]](/sites/default/files/tex_cache/dade002f849561ede809e0fa6ca6eaf0.png)
![\[\vdots\]](/sites/default/files/tex_cache/615ec350a1f8c235dbbc0c56a7c9d3d8.png)
![\[a_{k}= a_{k-1}+h; \]](/sites/default/files/tex_cache/586c5577bb721abacbeffb8f728e7a53.png)
![\[\vdots\]](/sites/default/files/tex_cache/615ec350a1f8c235dbbc0c56a7c9d3d8.png)
![\[a_{k}>x_{max}\]](/sites/default/files/tex_cache/56c5b6d65c971d991a32eef57342f9d1.png)
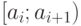 под-считываются значения
под-считываются значения 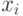 , отвечающие условию
, отвечающие условию 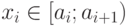
Рассмотрим пример. Пусть получены следующие значения плотности образцов горных пород:
| 2.58 | 2.65 | 2.52 | 2.68 | 2.70 | 2.73 | 2.71 | 2.58 | 2.49 |
| 2.50 | 2.73 | 2.68 | 2.64 | 2.68 | 2.72 | 2.73 | 2.78 | 2.78 |
| 2.77 | 2.59 | 2.53 | 2.59 | 2.62 | 2.51 | 2.52 | 2.64 | 2.65 |
Всего N=27. Ранжируем ряд
| Варианты | 2.49 | 2.50 | 2.51 | 2.52 | 2.53 | 2.58 | 2.59 | 2.62 |
| Частоты | 1 | 1 | 1 | 2 | 1 | 2 | 2 | 1 |
| Вероятность | 1/27 | 1/27 | 1/27 | 2/27 | 1/27 | 2/27 | 2/27 | 1/27 |
| Варианты | 2.64 | 2.65 | 2.68 | 2.7 | 2.71 | 2.72 | 2.73 | 2.78 |
| Частоты | 2 | 2 | 3 | 1 | 1 | 1 | 3 | 2 |
| Вероятность | 2/27 | 2/27 | 3/27 | 1/27 | 1/27 | 1/27 | 3/27 | 2/27 |
Выделено 16 вариант при длине ряда 27. Поэтому перейдем к непрерывному распределению, воспользовавшись коэффициентом Стэрджеса (12):
![\[h=\frac { 2,78-2,49 } {1+3,322 \cdot 3,3 } \approx 0,025 \approx 0,03\]](/sites/default/files/tex_cache/61e2ccd7cd355ce250473730c227a085.png) |
( 12) |
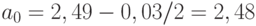 :
:| N п/п | 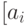 |
Значения 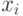 , входящие в интервал , входящие в интервал |
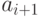 |
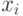 |
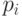 |
|---|---|---|---|---|---|
| 0 | 2,47 | 2,50 | 2,49 | 1 | 1/27 |
| 1 | 2,50 | 2,53 | 2,50;2.51;2.52 | 4 | 4/27 |
| 2 | 2,53 | 2,56 | 2,53 | 1 | 1/27 |
| 3 | 2,56 | 2,59 | 2,58 | 2 | 2/27 |
| 4 | 2,59 | 2,62 | 2,59 | 2 | 2/27 |
| 5 | 2,62 | 2,65 | 2,62;2.64 | 3 | 3/27 |
| 6 | 2,65 | 2,68 | 2,65 | 2 | 2/27 |
| 7 | 2,68 | 2,71 | 2,68;2.70 | 4 | 4/27 |
| 8 | 2,71 | 2,74 | 2,71;2.72;2.73 | 5 | 5/27 |
| 9 | 2,74 | 2,77 | - | 0 | 0 |
| 10 | 2,77 | 2,80 | 2,78 | 2 | 2/27 |
В результате оказалось, что ряд разбит только на 10 интервалов; вместо 16, что в конечном итоге ведет к уменьшению вычислений.
Второй способ рекомендуется для коротких рядов ( 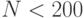 ). В этом случае задается не шаг, а количество интервалов разбиения. Как правило, выбирают 10 интервалов. Тогда шаг разбиения вычисляется по приближенной формуле
). В этом случае задается не шаг, а количество интервалов разбиения. Как правило, выбирают 10 интервалов. Тогда шаг разбиения вычисляется по приближенной формуле
 |
( 13) |
Если вернуться к нашему примеру, то
![\[h=\frac { 2,78 -2,49 } {10 }=\frac {0,29} {10} = 0,029 \approx 0,03, \]](/sites/default/files/tex_cache/f7ee0bfa0579ef767cf0d80b8a91f637.png)
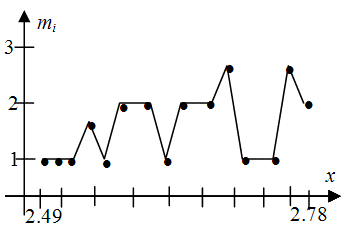
Если теперь по оси ОХ отложить варианты, а по оси OY - частоты, то, используя уже рассмотренный пример, получим следующие графики для дискретного (рис.1) и непрерыв-ного (рис.2) распределений.
Полигон частот и гистограмма описывают распределение частот 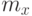 , определяемых для каждого значения случайной величины. При построении этих графиков не существует строгих методов выбора конечного числа интервалов или значений, однако рекомендуют, если
, определяемых для каждого значения случайной величины. При построении этих графиков не существует строгих методов выбора конечного числа интервалов или значений, однако рекомендуют, если 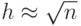 переходить от дискретного к непрерывному распределению.
переходить от дискретного к непрерывному распределению.
В заключении отметим, что довольно часто по оси OY откладывают значения 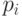 вместо
вместо