Лекция 12: Сходимость последовательностей случайных величин
Сходимости "почти наверное" и "по вероятности"
Напомним, что случайная величина есть (измеримая)
функция из некоторого непустого множества  в множество действительных чисел.
Последовательность случайных величин
в множество действительных чисел.
Последовательность случайных величин  есть
тем самым последовательность
функций, определенных на одном и том же множестве
есть
тем самым последовательность
функций, определенных на одном и том же множестве  .
Существуют разные виды сходимости последовательности
функций. Давать определение любой сходимости мы будем,
опираясь на сходимость числовых
последовательностей, как на уже известное основное понятие.
.
Существуют разные виды сходимости последовательности
функций. Давать определение любой сходимости мы будем,
опираясь на сходимость числовых
последовательностей, как на уже известное основное понятие.
В частности, при каждом новом  мы имеем новую числовую последовательность
мы имеем новую числовую последовательность  Поэтому можно говорить
о сходимости последовательности значений функций в данной точке
Поэтому можно говорить
о сходимости последовательности значений функций в данной точке 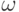 , а также во всех остальных точках
, а также во всех остальных точках  .
В теории вероятностей можно не обращать внимание на неприятности, происходящие
с нулевой вероятностью. Поэтому вместо сходимости
"всюду" принято рассматривать сходимость "почти
всюду", или "почти наверное".
.
В теории вероятностей можно не обращать внимание на неприятности, происходящие
с нулевой вероятностью. Поэтому вместо сходимости
"всюду" принято рассматривать сходимость "почти
всюду", или "почти наверное".
Определение 42.
Говорят, что последовательность  сходится
почти наверное к случайной величине
сходится
почти наверное к случайной величине  при
при  ,
и пишут:
,
и пишут:  п.н.,
если
п.н.,
если  .
Иначе говоря, если
.
Иначе говоря, если  при
при  для
всех
для
всех  , кроме, возможно,
, кроме, возможно,  , где
, где  - событие, имеющее нулевую
вероятность.
- событие, имеющее нулевую
вероятность.
Заметим сразу: определение сходимости "почти наверное"
требует знания того, как устроены
отображения  . В задачах же теории
вероятностей, как правило, известны не сами случайные величины, а
лишь их распределения.
. В задачах же теории
вероятностей, как правило, известны не сами случайные величины, а
лишь их распределения.
Можем ли мы, обладая только информацией о распределениях,
говорить о какой-либо сходимости последовательности случайных
величин  к случайной величине
к случайной величине  ?
?
Можно, скажем, потребовать, чтобы вероятность тех
элементарных исходов 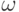 , для которых
, для которых 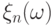 не попадает
в "
не попадает
в "  -окрестность" числа
-окрестность" числа  ,
уменьшалась до нуля
с ростом
,
уменьшалась до нуля
с ростом  . Такая сходимость в функциональном анализе называется
сходимостью "по мере", а в теории вероятностей -
сходимостью "по вероятности".
. Такая сходимость в функциональном анализе называется
сходимостью "по мере", а в теории вероятностей -
сходимостью "по вероятности".
Определение 42.
Говорят, что последовательность случайных величин  сходится
по вероятности к случайной величине
сходится
по вероятности к случайной величине  при
при  , и пишут
, и пишут  , если для любого
, если для любого 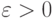

Пример 70.
Рассмотрим последовательность  , в которой
все величины имеют разные распределения: величина
, в которой
все величины имеют разные распределения: величина  принимает значения
принимает значения  и
и  с вероятностями
с вероятностями 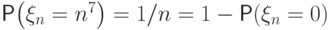 .
Докажем, что эта последовательность сходится по вероятности к нулю.
.
Докажем, что эта последовательность сходится по вероятности к нулю.
Зафиксируем произвольное 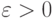 . Для
всех
. Для
всех  начиная с некоторого
начиная с некоторого  такого, что
такого, что  ,
верно равенство
,
верно равенство  .
Поэтому
.
Поэтому
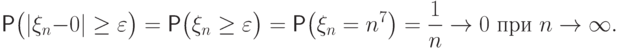
 с ростом
с ростом  могут принимать все большие и большие значения,
но со все меньшей и меньшей вероятностью.
могут принимать все большие и большие значения,
но со все меньшей и меньшей вероятностью.Например, последовательность  можно задать на
вероятностном пространстве
можно задать на
вероятностном пространстве ![\langle\Omega,\,\mathcal F,\,\Prob\rangle=
\langle [0,\,1],\,\mathfrak{B}([0,\,1]),\,\lambda\rangle](/sites/default/files/tex_cache/cf1718b0638c966e1deca0a6a72a5cdd.png) так:
положим
так:
положим 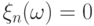 для
для ![\omega\in[0,\,1-1\mspace{1mu}/\,n]](/sites/default/files/tex_cache/87bcf7ba472726b656dda22c332c3d06.png) и
и  для
для ![\omega\in(1-1\mspace{1mu}/\,n,\,1]](/sites/default/files/tex_cache/87c8f28d6ba46a95d46887b66f2c8f27.png) .
.
Заметим, что сходимость по вероятности имеет место совершенно независимо
от того, как именно заданы случайные величины на  ,
поскольку
определяется лишь их распределениями.
,
поскольку
определяется лишь их распределениями.
Замечание
Иное дело - сходимость "почти наверное".
Если, скажем, задать случайные величины как указано выше,
то сходимость "почти наверное" будет иметь место.
Действительно,
для всякого  найдется такое
найдется такое  , что
, что ![\omega \in [0, 1-1/n_0]](/sites/default/files/tex_cache/ac522c00717511a4c73f57c9b991b7d8.png) , и поэтому
для всех
, и поэтому
для всех  все
все 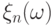 равны нулю.
равны нулю.
Можно попробовать задать случайные величины  на отрезке
на отрезке ![[0,\,1]](/sites/default/files/tex_cache/3c677f273d5640cb290c4e4ac717fbc7.png) как-нибудь
иначе, чтобы не было сходимости почти наверное. Для этого нужно заставить
отрезок длины
как-нибудь
иначе, чтобы не было сходимости почти наверное. Для этого нужно заставить
отрезок длины  , на котором
, на котором  ,
"бегать" по
отрезку
,
"бегать" по
отрезку ![[0,\,1]](/sites/default/files/tex_cache/3c677f273d5640cb290c4e4ac717fbc7.png) , чтобы любая точка
, чтобы любая точка ![\omega\in[0,\,1]](/sites/default/files/tex_cache/6267c165bba32251c965f3413a53ecac.png) попадала внутрь этого
отрезка бесконечное число раз, и, тем самым, для любого
попадала внутрь этого
отрезка бесконечное число раз, и, тем самым, для любого 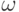 существовала подпоследовательность
существовала подпоследовательность  .
.
Сходимость по вероятности не обязательно сопровождается сходимостью
математических ожиданий или моментов других порядков:
из  не следует, что
не следует, что  .
Действительно,
в примере 70 имеет место
сходимость
.
Действительно,
в примере 70 имеет место
сходимость  ,
но
,
но  . При этом вообще
последовательность
. При этом вообще
последовательность  неограниченно возрастает.
неограниченно возрастает.
А если вместо значения  взять
взять  (с той же вероятностью
(с той же вероятностью  ),
то получим
),
то получим  . Но теперь хотя бы
предел у
последовательности математических ожиданий конечен.
. Но теперь хотя бы
предел у
последовательности математических ожиданий конечен.
Если же  принимает значения
принимает значения  и
и  с вероятностями
из примера 70, то
с вероятностями
из примера 70, то  , но уже вторые моменты
сходиться ко второму моменту
, но уже вторые моменты
сходиться ко второму моменту  не будут:
не будут:  .
.
Однако сходимость математических ожиданий и других моментов сходящихся
последовательностей
бывает чрезвычайно важна в различных задачах статистики.
Существуют условия, при выполнении которых сходимость по вероятности  влечет сходимость математических ожиданий
влечет сходимость математических ожиданий 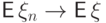 .
.
Сформулируем без доказательства следующее утверждение.
