Случайные величины и их распределения
Случайные величины
Мы уже видели, что для многих экспериментов нет никаких различий в подсчете вероятностей событий, тогда как элементарные исходы в этих экспериментах очень различаются. Но нас и должны интересовать именно вероятности событий, а не структура пространства элементарных исходов. Поэтому пора во всех таких "похожих" экспериментах вместо самых разных исходов использовать, например, числа. Иначе говоря, каждому элементарному исходу поставить в соответствие некоторое вещественное число, и работать только с числами.
Пусть задано вероятностное пространство  .
.
Определение 20.
Функция  называется случайной
величиной если для любого борелевского множества
называется случайной
величиной если для любого борелевского множества 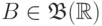 множество
множество 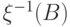 является событием, т.е. принадлежит
является событием, т.е. принадлежит 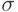 -алгебре
-алгебре 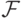 .
.
Множество  ,
состоящее из тех элементарных исходов
,
состоящее из тех элементарных исходов 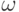 ,
для которых
,
для которых  принадлежит
принадлежит  , называется
полным
прообразом множества
, называется
полным
прообразом множества  .
.
Замечание.
Вообще, пусть функция  действует из множества
действует из множества  в множество
в множество  , и заданы
, и заданы 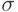 -алгебры
-алгебры  и
и  подмножеств
подмножеств  и
и  соответственно. Функция
соответственно. Функция  называется измеримой,
если для любого множества
называется измеримой,
если для любого множества 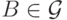 его полный прообраз
его полный прообраз  принадлежит
принадлежит  .
.
Попробуем понять, зачем случайной величине нужна измеримость.
Если задана случайная величина  , нам может потребоваться
вычислить
вероятности вида
, нам может потребоваться
вычислить
вероятности вида  ,
, ![\Prob(\xi\in[-3,\,7])](/sites/default/files/tex_cache/686f32ee8a8cbd03e468d156e37df1fe.png) ,
,  ,
,  и вообще самые разные
вероятности попадания в борелевские множества на прямой.
Это возможно лишь если множества, стоящие под знаком вероятности,
являются событиями - ведь
вероятность есть функция, определенная только на
и вообще самые разные
вероятности попадания в борелевские множества на прямой.
Это возможно лишь если множества, стоящие под знаком вероятности,
являются событиями - ведь
вероятность есть функция, определенная только на 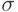 -алгебре
событий.
Требование измеримости равносильно тому, что для любого борелевского множества
-алгебре
событий.
Требование измеримости равносильно тому, что для любого борелевского множества  определена вероятность
определена вероятность  .
.
Можно потребовать в определении 20 чего-нибудь другого.
Например, чтобы событием было попадание в любой интервал:  ,
или в любой полуинтервал:
,
или в любой полуинтервал:  .
.
Определение 21.
Функция  называется случайной величиной,
если для любых вещественных
называется случайной величиной,
если для любых вещественных 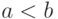 множество
множество  принадлежит
принадлежит 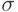 -алгебре
-алгебре  .
.
Доказательство. Докажем эквивалентность определений 20 и 21.
Если  - случайная величина в смысле определения 20, то
она будет случайной величиной и в смысле определения 21,
поскольку любой интервал
- случайная величина в смысле определения 20, то
она будет случайной величиной и в смысле определения 21,
поскольку любой интервал 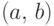 является борелевским множеством.
является борелевским множеством.
Докажем, что верно и обратное.
Пусть для любого интервала  выполнено
выполнено  .
Мы должны доказать, что то же самое верно
для любых борелевских множеств. Соберем в множестве
.
Мы должны доказать, что то же самое верно
для любых борелевских множеств. Соберем в множестве  все
такие подмножества
все
такие подмножества  вещественной прямой, что их прообразы
являются
событиями. По определению,
вещественной прямой, что их прообразы
являются
событиями. По определению,  тогда и только тогда,
когда множество
тогда и только тогда,
когда множество 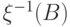 принадлежит
принадлежит 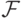 .
.
Множество 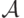 уже содержит все интервалы
уже содержит все интервалы 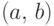 .
Покажем, что множество
.
Покажем, что множество 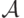 является
является 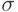 -алгеброй.
-алгеброй.
- Убедимся, что
 . Но
. Но  и, следовательно,
и, следовательно,  .
. - Убедимся, что
 для любого
для любого  .
Пусть
.
Пусть  . Тогда
. Тогда 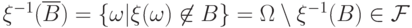 , так как
, так как  -
- 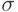 -алгебра.
-алгебра. - Убедимся, что
 для любых
для любых  .
Пусть
.
Пусть  для всех
для всех  .
Но
.
Но  -
- 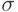 -алгебра, поэтому
-алгебра, поэтому
Мы доказали, что 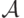 -
- 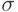 -алгебра и
содержит все интервалы
на прямой. Но
-алгебра и
содержит все интервалы
на прямой. Но  - наименьшая из
- наименьшая из 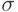 -алгебр,
содержащих все интервалы на прямой. Следовательно,
-алгебр,
содержащих все интервалы на прямой. Следовательно,  .
.
Приведем примеры измеримых и неизмеримых функций.
Пример 37.
Подбрасываем кубик. Пусть 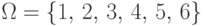 и две функции
из
и две функции
из  в
в  заданы так:
заданы так:  ,
,  .
.
Пока не задана 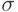 -алгебра
-алгебра  ,
нельзя говорить
об измеримости. Функция, измеримая относительно какой-то
,
нельзя говорить
об измеримости. Функция, измеримая относительно какой-то 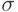 -алгебры
-алгебры  ,
может не быть таковой для другой
,
может не быть таковой для другой  .
.
- Если
 есть множество всех подмножеств
есть множество всех подмножеств  , то
, то  и
и  являются
случайными величинами,
поскольку любое множество элементарных исходов принадлежит
являются
случайными величинами,
поскольку любое множество элементарных исходов принадлежит 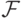 ,
в том числе и
,
в том числе и 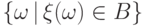 или
или  .
Можно записать соответствие между значениями случайных величин
.
Можно записать соответствие между значениями случайных величин  и
и  и вероятностями принимать эти значения в
виде
таблицы распределения вероятностей или, короче, таблицы
распределения:Здесь
и вероятностями принимать эти значения в
виде
таблицы распределения вероятностей или, короче, таблицы
распределения:Здесь
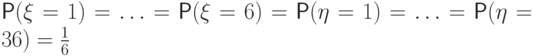 .
. - Пусть
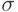 -алгебра событий
-алгебра событий  состоит из четырех множеств:т.е. событием является, кроме достоверного и невозможного событий, выпадение четного или нечетного числа очков. Убедимся, что при такой сравнительно бедной
состоит из четырех множеств:т.е. событием является, кроме достоверного и невозможного событий, выпадение четного или нечетного числа очков. Убедимся, что при такой сравнительно бедной
( 6.1) 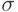 -алгебре ни
-алгебре ни  , ни
, ни  ,
не являются случайными величинами. Возьмем, скажем,
,
не являются случайными величинами. Возьмем, скажем, 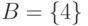 .
Видим, что
.
Видим, что  и
и  .
.
Пример 38.
Пусть ![\Omega=[0,\,2\pi]](/sites/default/files/tex_cache/19a534ae49e43e257af2eea7d0fe61d8.png) ,
, ![\mathcal
F=\mathfrak{B}(\mathbb R)\cap[0,\,2\pi]](/sites/default/files/tex_cache/377852386d57ee36ee01ca07fe0b3923.png) - сигма-алгебра борелевских
подмножеств отрезка
- сигма-алгебра борелевских
подмножеств отрезка ![[0,\,2\pi]](/sites/default/files/tex_cache/59361ead5ae637680a2e00871398c150.png) ,
,  -
геометрическая вероятность на
-
геометрическая вероятность на  и
и  - неизмеримое множество Витали, построенное нами
в примере 21.
Функция
- неизмеримое множество Витали, построенное нами
в примере 21.
Функция

 не принадлежит
не принадлежит 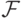 .
И вероятность для
.
И вероятность для  попасть в единицу
попасть в единицу  просто не существует.
просто не существует.Познакомимся с важным понятием - "распределение" случайной величины и опишем различные типы распределений случайных величин.
