Логические основы компьютера
Битовые операции
Битовые операции, операндами которых являются входные цифровые сигналы, лежат в основе логики работы электронных логических устройств. Они реализованы во многих языках программирования высокого уровня.
Битовыми называют операции над цепочками битов. Основными битовыми операциями являются побитовые операции и битовые сдвиги.
Побитовые операции
Побитовые операции - это операции, которые применяются к каждому биту из цепочки битов. Основными побитовыми операциями являются побитовое отрицание bitNot, побитовая конъюнкция bitAnd, побитовая дизъюнкция bitOr и побитовая строгая дизъюнкция bitXor.
Для того, чтобы найти результат побитовой операции, следует представить числа в двоичном виде и затем применить операцию к цифрам, стоящим в одинаковых разрядах.
Побитовая операция отрицания соответствует побитовому применению функции inv(x) = 1 - x, для 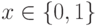 .
.
Пример 22. Пусть для хранения чисел используется 4 байта. Тогда 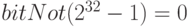 . Соответственно,
. Соответственно, 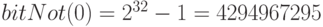 .
.
Найдем результат побитовой операции отрицания, примененной к числу 275. Имеем:  , или в 4 байтах,
, или в 4 байтах,
00000000 00000000 00000001 00010011.
Применив к каждому биту функцию inv(x) = 1 - x, получим:
11111111 11111111 11111110 11101100.
Таким образом, bitNot(275) = 4294967020.
Побитовые операции конъюнкции, дизъюнкции и строгой дизъюнкции соответствуют побитовому применению функций
f(x, y) = min(x, y), g(x, y) = max(x, y), h(x, y) = (x + y) mod 2,
соответственно, где  .
.
Пример 23. Найдем результаты применения побитовых бинарных операций к числам 14 и 26. Имеем: 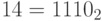 ,
, 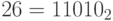 . Поэтому
. Поэтому
Следовательно,
bitAnd(14, 26) = 10; bitOr(14, 26) = 30; bitXor(14, 26) = 20.
Обозначим через Deg(x) множество показателей степеней 2 в разложении числа x по степеням 2. Тогда
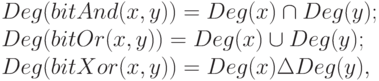
где символами  ,
,  и
и  обозначены операции пересечения, объединения и симметрической разности множеств, соответственно.
обозначены операции пересечения, объединения и симметрической разности множеств, соответственно.
Пример 24. Пусть x = 15, y = 28. Тогда
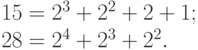
Поэтому Deg(15) = {0, 1, 2, 3}, Deg(28) = {2, 3, 4}. Имеем:
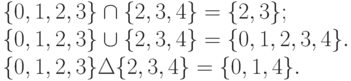
Следовательно,
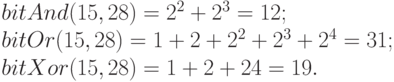
Ясно, что операции объединения, пересечения и симметрической разности могут применяться к самим степеням 2. В данном случае имеем:
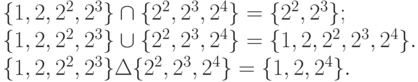
Свойства операции bitXor рассматриваются также в п. 5.1.
Битовые сдвиги
Битовые сдвиги разделяют на арифметические и логические. Первые зависят, а вторые не зависят от числа разрядов, которые используются для представления числа. В языках программирования реализуются логические сдвиги.
Пусть двоичное представление целого неотрицательного числа x имеет вид: 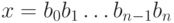 . Тогда операции арифметических битовых сдвигов определяются следующим образом:
. Тогда операции арифметических битовых сдвигов определяются следующим образом:
 - арифметический сдвиг влево;
- арифметический сдвиг влево;
 - арифметический сдвиг вправо.
- арифметический сдвиг вправо.
Пусть число разрядов, используемых в типе данных, равно (n + 1). Тогда операции логических битовых сдвигов определяются в виде:
 - логический сдвиг влево;
- логический сдвиг влево;
 - логический сдвиг вправо.
- логический сдвиг вправо.
Обозначим через bitShiftLeft и bitShiftRight - операции арифметических сдвигов влево и вправо, соответственно, а через bitLeft и bitRight - операции логических сдвигов соответственно влево и вправо.
Нетрудно заметить, что
bitShiftLeft(x) = 2x; bitShiftRight(x) = bitRight(x) = x div 2
(см. п. 1.1). Таким образом, арифметический сдвиг влево соответствует удвоению числа. Кроме того, заметим, что если число x - четное, а в этом случае его младший разряд равен 0, то в результате сдвига вправо получится число, ровно в 2 раза меньшее исходного. Если же младший разряд числа равен 1, то получится целая часть частного от деления на 2.
В типах данных число разрядов фиксировано, поэтому при логическом сдвиге влево теряется старший разряд. Найдем число, которое получается при логическом сдвиге числа x влево на 1 разряд, если число разрядов в типе данных равно n + 1.
Имеем: 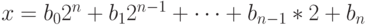 . Поэтому
. Поэтому
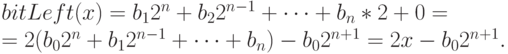
Таким образом, если старший разряд числа x равен 0, то логический сдвиг влево приведет к удвоению числа. Далее, старший разряд числа x, для 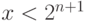 , равен 1, если
, равен 1, если  . Пусть
. Пусть 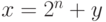 , где
, где 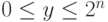 . Тогда
. Тогда  . Следовательно, если старший разряд числа равен 1, то в результате его логического сдвига влево получится его удвоенный остаток от деления на
. Следовательно, если старший разряд числа равен 1, то в результате его логического сдвига влево получится его удвоенный остаток от деления на 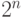 .
.
Пример 24. Пусть тип данных содержит 4 байта.
Для числа 23 имеем:
bitShiftLeft(23) = bitLeft(23) = 46; bitShiftRight(23) = bitRight(23) = 11,
что легко получить из определения операций, так как 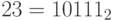 .
.
Найдем сдвиг влево для максимального числа. Имеем:

Таким образом, bitLeft(4294967295) = 4294967294.
В общем случае, пусть число разрядов равно n + 1 и 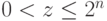 . Тогда
. Тогда 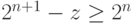 . Поэтому
. Поэтому
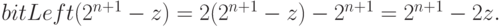
В частности, если тип данных содержит 4 байта, то  , а для арифметического сдвига имеем:
, а для арифметического сдвига имеем:  .
.
Рассмотрим битовые сдвиги на k разрядов, где  . Покажем, что арифметический сдвиг влево на k разрядов числа x соответствует умножению x на
. Покажем, что арифметический сдвиг влево на k разрядов числа x соответствует умножению x на 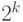 . Арифметический сдвиг вправо на k разрядов числа x приводит к целой части частного от деления x на
. Арифметический сдвиг вправо на k разрядов числа x приводит к целой части частного от деления x на 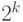 .
.
Пусть опять представление целого неотрицательного числа x в двоичном виде имеет вид: x = b0b1 \dots bn - 1bn. Тогда арифметический битовый сдвиг на k разрядов влево определяется следующим образом:

Ясно, что 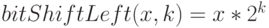 .
.
Пример 25. Для числа 5 имеем:
bitShiftLeft(5, 1) = 10; bitShiftLeft(5, 2) = 20; bitShiftLeft(5, 3) = 40; bitShiftLeft(5, 4) = 80.
Соответственно,

Арифметический и логический битовые сдвиги на k разрядов вправо совпадают и определяются следующим образом:

Пусть  . Имеем:
. Имеем:
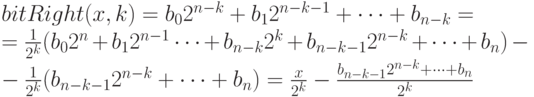
Следовательно, 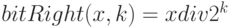 .
.
Пример 26. 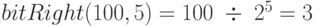 .
.
Пусть тип данных содержит n + 1 разряд. Определение логического сдвига влево на k разрядов имеет вид:
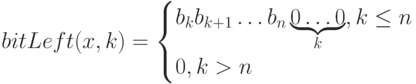
Пусть  . Тогда
. Тогда
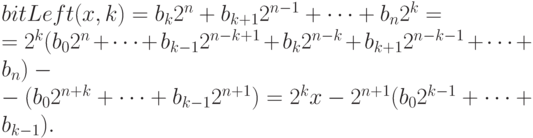
Пример 27. Рассмотрим битовые сдвиги числа 14 на 2 разряда влево и вправо. Имеем: 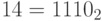 , n = 3, k = 2.
, n = 3, k = 2.
Арифметический сдвиг влево на 2 разряда:  .
.
Логический сдвиг вправо на 2 разряда:
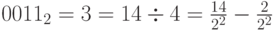
Логический сдвиг влево на 2 разряда:
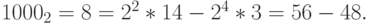
Пример 28. Пусть тип данных содержит 4 байта. Рассмотрим логический сдвиг максимального числа влево на k разрядов, для 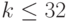 . Имеем:
. Имеем:
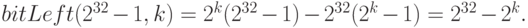
Например,
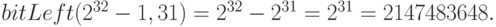
В компьютерной программе двоичное представление числа можно преобразовать в десятичное представление с помощью битовых сдвигов единицы влево и побитовой дизъюнкции, которая обобщается на произвольное число аргументов.
Пример 29. Для числа  имеем:
имеем:
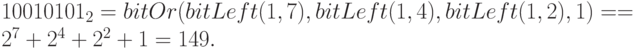
Пример 30. Вычислим bitOr(bitShiftLeft(5, 2), bitShiftLeft(3, 1)).
Имеем:
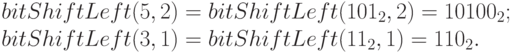
Поэтому  .
.
Упражнения
-
Определите, является ли высказыванием предложение
a) "Проверьте напряжение в электросети";
b) "Что посеешь, то и пожнешь";
c) "Земля вращается вокруг Солнца";
d) "Это предложение ложное".
-
Составьте из высказываний A: "Идет дождь" и B: "Мы сидим дома" высказывание
a) A & B;
b)
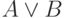 ;
;c)
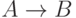 ;
;d)
 ;
;e)
 ;
;f)
 ;
;g)
 ;
;h)
 .
. -
Составьте из высказываний A: "Идет дождь" и B: "Мы сидим дома" сложное высказывание, которое является
a) тавтологией;
b) противоречием.
-
Определите, является ли тавтологией высказывание
a)
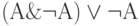 ;
;b)
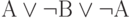 ;
;c)
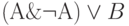 ;
;d)
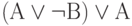 .
. -
Составьте таблицу истинности для высказывания
a)
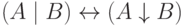 ;
;b)
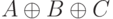 .
. -
Упростите выражение
a)
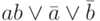 ;
;b)
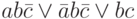 ;
;c)
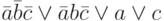 ;
;d)
 .
. -
Покажите, что в произвольной булевой алгебре верно равенство
a)
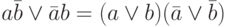 ;
; b)
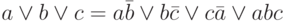 .
. -
Используя свойства логических операций, решите задачу.
Сестры Маша, Даша и Глаша испекли пирог. Одна из них месила тесто, другая готовила начинку, а третья выпекала пирог. Известно, что каждое из следующих высказываний истинно:
- если Глаша месила тесто, то Даша готовила начинку;
- если Маша выпекала пирог, то месила тесто Даша;
- если Глаша готовила начинку, то Маша выпекала пирог;
- если Даша месила тесто, то Маша готовила начинку;
- если Глаша выпекала пирог, то Маша месила тесто.
Кто из них месил тесто, кто готовил начинку, а кто выпекал пирог?
-
Составьте для логической функции таблицу истинности и постройте по ней 1) СДНФ; 2) СКНФ, если функция на множестве {0, 1} определяется следующим образом:
a)
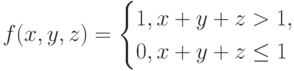
b)
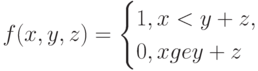
-
Постройте электронную логическую схему для функции
a)
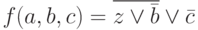
b)
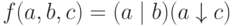 .
. - Составьте таблицу истинности и постройте электронную логическую схему для одноразрядного полусумматора (см. пример 21).
-
Постройте электронные логические схемы для логической операции 1) конъюнкции; 2) дизъюнкции; 3) отрицания; 4) строгой дизъюнкции; 5) эквиваленции, используя только
a) схему И-НЕ;
b) схему ИЛИ-НЕ.
- Постройте электронные логические схемы для функций из упр. 4.9.
-
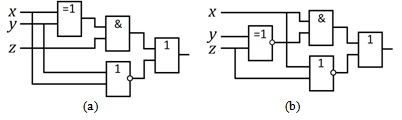
Постройте логическую функцию по электронной логической схеме
a) рис. 4.14 (a); b) рис. 4.14 (b). -
Вычислите результат побитовой операции отрицания, если тип данных использует для хранения чисел 4 байта, для числа
a) 33;
b)
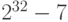 .
. -
Вычислите результат побитовой операции:
a) bitAnd(7, 8);
b) bitOr(16, 1);
c) bitXor(9, 9);
d) bitAnd(17, 23);
e) bitOr(17, 23);
f) bitXor(17, 23);
g) bitAnd(100, 10);
h) bitOr(25, 5);
i) bitXor(0, 10).
-
Вычислите результат арифметического битового сдвига
a) bitShiftLeft(33);
b) bitShiftRight(19, 2).
-
Вычислите результат логического битового сдвига числа x на k разрядов влево для типа данных с 32 разрядами:
a)
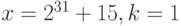 ;
;b)
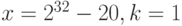 ;
;c) x = 70, k = 5;
d)
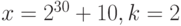 .
. - Вычислите bitOr(bitLeft(6, 3), bitLeft(10, 2), bitLeft(7, 1)).
- Вычислите bitAnd(bitRight(26, 3), bitRight(17, 4)).