|
как начать заново проходить курс, если уже пройдено несколько лекций со сданными тестами? |
Алгоритмы с открытыми ключами
8.2 Атаки на алгоритм RSA
Для расшифрования необходимо по известным  ,
,  и шифртексту
и шифртексту  найти такое
найти такое 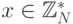 , что
, что 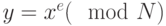 .
.
Попытаемся решить сравнение при конкретных  , затем использовать гомоморфность отображения
, затем использовать гомоморфность отображения 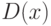 .
.
Один из возможных способов следующий: пусть имеется набор пар:

с условием, что  ,
, 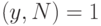 . Если каким-либо образом удалось представить
. Если каким-либо образом удалось представить  в виде
в виде 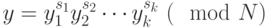 с целыми
с целыми 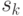 , то
, то 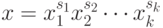 будет решением сравнения
будет решением сравнения 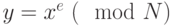 .
.
Пример 8.3 В наличии имеется открытый ключ 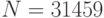 ,
,  и набор пар соответствующих друг другу исходных и зашифрованных сообщений:
и набор пар соответствующих друг другу исходных и зашифрованных сообщений:  ,
, 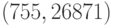 ,
, 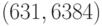 . Требуется расшифровать шифртекст
. Требуется расшифровать шифртекст 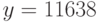 .
.
Представим  в виде
в виде 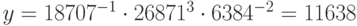 . Отсюда легко вычислить исходное сообщение:
. Отсюда легко вычислить исходное сообщение: 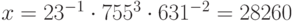 .
.
Заметим, что этот подход не менее труден, чем поиск алгоритма решения сравнения 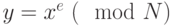 .
.
Взлом RSA при неудачном выборе параметров криптосистемы
Само по себе использование RSA не обеспечивает безопасности. Дело еще в деталях реализации. Приведем ряд примеров. Для простоты вычислений будем работать с небольшими числами. Цель - показать особенности, не зависящие от размера.
Пример 8.4 Пусть пользователь выбрал 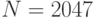 ,
,  ,
,  . Так как
. Так как 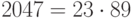 , а числа
, а числа  и
и  имеют наименьшее общее кратное 88, то любое обратное к 179 по модулю 88, например 59, будет действовать как
имеют наименьшее общее кратное 88, то любое обратное к 179 по модулю 88, например 59, будет действовать как 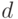 .
.
Пример 8.5 Число  является произведением простого числа Мерсенна
является произведением простого числа Мерсенна  и простого числа Ферма
и простого числа Ферма 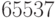 . Это очень плохой выбор.
. Это очень плохой выбор.
Пример 8.6 Число  является очень плохим выбором для
является очень плохим выбором для  из-за того, что два его простых делителя слишком близки к друг другу.
из-за того, что два его простых делителя слишком близки к друг другу.
Пусть  , тогда имеем:
, тогда имеем:
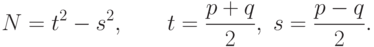
Так как  мало, то
мало, то  - целое число, лишь немного большее
- целое число, лишь немного большее  , причем
, причем  является полным квадратом. Проверяем подряд целые числа
является полным квадратом. Проверяем подряд целые числа 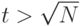 . В нашем примере это
. В нашем примере это  ,
,  ,
, 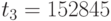 , причем
, причем 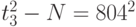 . Тогда
. Тогда  . Таким образом, мы с третьей попытки нашли
. Таким образом, мы с третьей попытки нашли  и
и  . Количество попыток, необходимых для факторизации
. Количество попыток, необходимых для факторизации  , можно при известных
, можно при известных  и
и  вычислить по следующей формуле:
вычислить по следующей формуле:
![k=\sqrt{p\cdot q + \left(\frac{p-q}{2}\right)^2}-\left[\sqrt{p\cdot q}\right],](/sites/default/files/tex_cache/e4d9ee344fad87086f7d6202faa266f1.png)
где ![[x]](/sites/default/files/tex_cache/3e5314e9fd31509fdeb83faa0f729ba2.png) - операция округления
- операция округления  до ближайшего целого числа.
до ближайшего целого числа.
