Минимальные остовные деревья

Представления

В этой главе мы займемся взвешенными неориентированными графами — самой естественной средой для задачи MST. Наверно, проще всего начать с расширения базовых представлений графа из "Виды графов и их свойства" : в представлении матрицей смежности вместо логических значений могут быть проставлены веса ребер; в представлении списками смежности в элементы списка, представляющие ребра, можно добавить поле веса. Этот классический подход привлекает своей простотой, но мы будем пользоваться другим методом, который не намного сложнее, зато позволит использовать наши программы в более общих условиях. Сравнительные характеристики производительности этих подходов будут проведены ниже в данной главе.

Чтобы рассмотреть все вопросы, возникающие при переходе от графов, где нас интересует только наличие или отсутствие ребер, к графам, в которых нам важна информация, связанная с ребрами, удобно представить ситуации, где вершины и ребра представляют собой объекты неизвестной сложности. Возможно, они являются какой-то частью крупной базы данных клиентов, которая создана и используется другим приложением. Например, бывает нужно рассматривать улицы, дороги и автострады в географической базе данных как абстрактные ребра, где веса представляют их длины. Но записи базы данных могут содержать и другую информацию — например, название дороги и ее тип, подробное описание ее физических свойств, интенсивность движения и т.п. Клиентская программа может выбрать нужную информацию, построить граф, обработать его, а затем интерпретировать полученные результаты в контексте базы данных — но это может оказаться сложным и трудоемким процессом. В частности, для этого нужна (по меньшей мере) копия графа.

В клиентских программах удобнее определить тип данных EDGE, а в реализациях — работать с указателями на ребра. В программе 20.1 описаны абстрактные типы данных EDGE, GRAPH и итератора, которые нужны для этого подхода. Клиенты легко могут удовлетворить минимальные требования типа данных EDGE, позволяя при этом определять типы данных для использования в контекстах других приложений. Наши реализации могут работать с указателями на ребра и использовать интерфейс для извлечения необходимой им информации из объектов EDGE независимо от их представления. Пример клиентской программы, использующей этот интерфейс, приведен в программе 20.2.

При тестировании алгоритмов и в базовых приложениях мы будем использовать класс EDGE (ребро), содержащий два приватных члена данных типа int и один типа double, которые инициализируются аргументами конструктора и возвращаются, соответственно, функциями-членами v(), w() и wt() (см. упражнение 20.8). Для единообразия в этой главе и в главе 21 "Кратчайшие пути" мы будем представлять веса ребер типом данных double. В наших примерах в качестве весов ребер будут использоваться вещественные числа от 0 до 1. Это решение не противоречит различным вариантам, которые могут встретиться в приложениях, поскольку всегда можно явно или неявно масштабировать веса, чтобы они соответствовали этой модели (см. упражнения 20.1 и 20.10). Например, если весами являются положительные целые числа, меньшие известного максимального значения, то поделив значения весов на это максимальное значение, мы преобразуем их в вещественные числа из диапазона от 0 до 1.

При желании можно было бы разработать более общий интерфейс АТД и использовать для весов ребер любой тип данных, который поддерживает операции сложения, вычитания и сравнения, поскольку мы не только накапливаем суммы весов и принимаем решения в зависимости от их значений. В алгоритмах, которые будут рассмотрены в "Потоки в сетях" , понадобятся сравнения линейных комбинаций весов ребер, а время выполнения некоторых алгоритмов зависит от арифметических свойств весов, поэтому мы перейдем на целочисленные веса, чтобы упростить анализ алгоритмов.

Программы 20.2 и 20.3 реализуют АТД взвешенного графа из программы 20.1, представленного матрицей смежности. Как и раньше, для вставки ребра в неориентированный граф нужно занести указатели на него в двух местах матрицы — по одному для каждого направления ребра. Как обычно для алгоритмов, работающих с представлением неориентированных графов в виде матрицы смежности, их время выполнения пропорционально V² (на инициализацию матрицы) или выше.

Программа 20.1. Интерфейс АТД для графов со взвешенными ребрами

Этот код определяет интерфейс для графов с весами и другой информацией, связанной с ребрами. Он содержит интерфейс АТД ребра EDGE и шаблонный интерфейс графа GRAPH, которые можно использовать в любой реализации интерфейса EDGE. Реализации GRAPH работают с указателями на ребра (они берутся в клиентах из функции insert), а не самими ребрами. Класс ребер содержит также функции-члены, которые предоставляют информацию об ориентации ребра: либо e->from(v) истинно, e->v() равно v, а e->other(v) содержит e->w(); либо e->from(v) ложно, e->w() равно v, а e->other(v) содержит e->v().

  class EDGE {
    public:
      EDGE(int, int, double);
      int v() const;
      int w( ) const;
      double wt() const;
      bool from(int) const;
      int other(int) const;
  };
  template <class Edge>
  class GRAPH {
    public:
      GRAPH(int, bool);
      ~GRAPH();
      int V() const;
      int E() const;
      bool directed() const;
      int insert(Edge *);
      int remove(Edge *);
      Edge *edge(int, int);
      class adjIterator {
        public:
          adjIterator(const GRAPH &, int);
          Edge *beg();
          Edge *nxt();
          bool end();
       };
  };
      

Программа 20.2. Пример клиентской функции обработки графа

Данная функция демонстрирует применение интерфейса взвешенного графа из программы 20.1. При любой реализации этого интерфейса функция edges возвращает вектор, содержащий указатели на все ребра графа. Как и в главах 17—19, обычно функции итератора используются только так, как показано здесь.

  template <class Graph, class Edge>
  vector <Edge *> edges(const Graph &G)
    { int E = 0;
      vector <Edge *> a(G.E());
      for (int v = 0; v < G.V(); v++)
        { typename Graph::adjIterator A(G, v);
          for (Edge* e = A.beg(); !A.end(); e = A.nxt())
            if (e->from(v)) a[E++] = e;
        }
      return a;
    }
      

Проверка на существование ребра v-w при таком представлении сводится к проверке, является ли пустым указатель на пересечении строки v и столбца w. Иногда можно избежать таких проверок с помощью сигнальных значений для весов, однако в наших реализациях сигнальные значения использоваться не будут.

Программа 20.5 содержит детали реализации АТД взвешенного графа с указателями на ребра в представлении списками смежности. Вектор, индексированный именами вершин, ставит в соответствие каждой вершине связный список инцидентных ей ребер. Каждый узел списка содержит указатель на ребро. Как и в случае матрицы смежности, при желании можно сэкономить память, храня в узлах списков конечные вершины и веса (с неявным указанием исходной вершины), но за счет усложнения итератора (см. упражнения 20.11 и 20.14).

Программа 20.3. Класс взвешенного графа (матрица смежности)

Для насыщенных взвешенных графов мы используем матрицу указателей на данные типа Edge с указателем на ребро v-u в строке v и столбце w. Для неориентированных графов заносится еще один указатель на ребро — в строке w и столбце v. Пустой указатель означает отсутствие ребра; для удаления ребра функция remove() удаляет указатель на него. Данная реализация не выполняет проверку на наличие параллельных ребер, хотя клиенты могут воспользоваться для этого функцией edge.

  template <class Edge>
  class DenseGRAPH
    { int Vcnt, Ecnt; bool digraph;
      vector <vector <Edge *> > adj;
    public:
      DenseGRAPH(int V, bool digraph = false) :
        adj(V), Vcnt(V), Ecnt(0), digraph(digraph)
        { for (int i = 0; i < V; i++)
            adj[i].assign(V, 0);
        }
      int V() const { return Vcnt; }
      int E() const { return Ecnt; }
      bool directed() const { return digraph; }
      void insert(Edge *e)
        { int v = e->v(), w = e->w ();
          if (adj[v][w] == 0) Ecnt++;
          adj [ v] [ w] = e;
          if (!digraph) adj[w][v] = e;
        }
      void remove(Edge *e)
        { int v = e->v(), w = e->w ();
          if (adj[v][w] != 0) Ecnt —;
          adj[v][w] = 0;
          if (!digraph) adj[w][v] = 0;
        }
      Edge* edge(int v, int w) const
        { return adj[v][w]; }
      class adjlterator;
      friend class adjlterator;
    };
      

Программа 20.4. Класс итератора для представления матрицей смежности

Этот код, возвращающий указатели на ребра, является простой адаптацией программы 17.8.

  template <class Edge>
  class DenseGRAPH<Edge>::adjIterator
    { const DenseGRAPH<Edge> &G;
      int i, v;
    public:
      adjIterator(const DenseGRAPH<Edge> &G, int v) :
        G(G), v(v), i(0) { }
      Edge *beg()
        { i = -1; return nxt(); }
      Edge *nxt()
        { for (i++; i < G.V(); i++)
            if (G.edge(v, i)) return G.adj[v][i];
          return 0;
        }
      bool end() const
        { return i >= G.V(); }
    } ;
      

Программа 20.5. Класс взвешенного графа (списки смежности)

Данная реализация интерфейса из программы 20.1 основана на представлении графа в виде списков смежности и поэтому удобна для разреженных взвешенных графов. Как и в случае невзвешенных графов, каждое ребро представляется узлом списка, но здесь каждый узел содержит указатель на соответствующее ребро, а не просто на конечную вершину. Класс итератора представляет собой непосредственную адаптацию программы 17.10 (см. упражнение 20.13).

  template <class Edge>
  class SparseMultiGRAPH
    { int Vcnt, Ecnt; bool digraph;
      struct node
        { Edge* e; node* next;
          node(Edge* e, node* next): e(e), next(next) {}
        };
      typedef node* link;
      vector <link> adj;
    public:
      SparseMultiGRAPH(int V, bool digraph = false) :
        adj(V), Vcnt(V), Ecnt(0), digraph(digraph) { }
      int V() const { return Vcnt; }
      int E() const { return Ecnt; }
      bool directed() const { return digraph; }
      void insert(Edge *e)
        { adj[e->v()] = new node(e, adj[e->v()]);
          if (!digraph)
            adj[e->w()] = new node(e, adj[e->w()]);
          Ecnt++;
        }
      class adjIterator;
      friend class adjIterator;
    };
      

На этом этапе полезно сравнить эти представления с простыми представлениями, о которых шла речь в начале этого раздела (см. упражнения 20.11 и 20.12). Если строить граф с нуля, то, конечно, использование указателей потребовало бы большего объема памяти. Память нужна не только для размещения указателей, но и для индексов (имен вершин), которые в простых реализациях представлены неявно. Чтобы использовать указатели на ребра в представлении матрицей смежности, требуется дополнительный объем памяти для размещения V² указателей на ребра и E пар индексов. Аналогично, чтобы использовать указатели на ребра в представлении списками смежности, требуется дополнительный объем памяти для размещения E указателей на ребра и E индексов.

Однако использование указателей на ребра зачастую позволяет получить более быстрый код, поскольку скомпилированный код клиентской программы получает непосредственный доступ к весу через один указатель — в отличие от простой реализации, где сначала создается элемент типа Edge (ребро), а затем выполняется обращение к его полям. Если память критична, то применение минимальных представлений (и, возможно, оптимизация итераторов для экономии времени) может быть разумным вариантом, но в остальных случаях гибкость, которую дает применение указателей, стоит дополнительных затрат памяти.

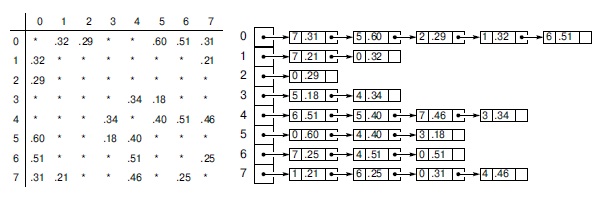
Однако на всех рисунках будут применяться простые представления, чтобы не загромождать их. То есть мы будем показывать не матрицы указателей на структуры ребер (пара целых чисел и вес), а просто матрицы весов, и вместо узлов списков с указателями на структуры ребер мы будем показывать узлы, содержащие конечные вершины ребер. Представления нашего демонстрационного графа в виде матрицы смежности и списков смежности приведены на рис. 20.3.

Что касается реализаций неориентированных графов, то ни в одной из реализаций не выполняется проверка на наличие параллельных ребер.

Рис. 20.3. Представления взвешенного графа (неориентированного)

Два стандартных представления взвешенных неориентированных графов содержат веса в каждом представлении ребра. Здесь показаны представления графа, изображенного на рис. 20.1, в виде матрицы смежности (слева) и в виде списков смежности (справа). Для простоты веса на этих рисунках показаны непосредственно в элементах матрицы и в узлах списков; в наших программах мы используем указатели на ребра, построенные клиентскими программами. Матрица смежности симметрична, а списки смежности содержат по два узла для каждого ребра, как и в случае невзвешенных ориентированных графов. Отсутствующие ребра представлены в матрице пустыми указателями (на рисунке — звездочками), а в списках их просто нет. В обоих представлениях нет петель, поскольку алгоритмы MSTбез них оказываются проще — хотя они используются другими алгоритмами обработки взвешенных графов (см. "Кратчайшие пути"

В зависимости от приложения можно изменить представление матрицей смежности так, чтобы сохранять параллельные ребра с наименьшим или наибольшим весом, либо сливать параллельные ребра в единое ребро с весом, равным сумме весов параллельных ребер. В представлении списками смежности параллельные ребра могут присутствовать в структуре данных, хотя можно построить более совершенные структуры данных, позволяющие отказаться от них с помощью одного из правил, описанных для матриц смежности (см. упражнение 17.49).

А как представить само MST-дерево? MST-дерево графа G — это подграф графа G, который сам по себе является деревом, поэтому возможны различные варианты, основными из которых являются:

• Граф.
• Связный список ребер.
• Вектор указателей на ребра.
• Вектор, индексированный именами вершин, с родительскими ссылками.

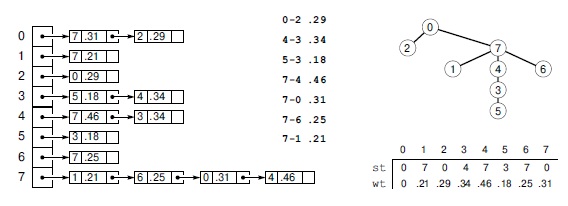
На рис. 20.4 показаны эти варианты для MST-дерева с рис. 20.1. Еще один вариант — определить и использовать АТД для деревьев.

Одно и то же дерево может иметь различные представления в любой из указанных выше схем. В каком порядке следует хранить ребра в представлении списком ребер? Какой узел выбрать в качестве корня в представлении родительскими ссылками (см. упражнение 20.21)? Вообще-то конкретное представление MST-дерева, которое получается при выполнении алгоритма MST, зависит только от используемого алгоритма и не отражает никаких важных свойств MST-дерева.

Рис. 20.4. Представления MST-дерева

Здесь показаны различные представления MST-дерева с рис. 20.1. Наиболее простым является список его ребер в произвольном порядке (слева). MST-дерево — это разреженный граф, и его можно представить списками смежности (в центре). Наиболее компактным является представление родительскими ссылками: одна из вершин выбирается в качестве корня, и используются два вектора, индексированные именами вершин: один содержит родительский узел для каждой вершины дерева, а второй — вес ребра, ведущего из данной вершины к ее родителю (справа). Ориентация дерева (выбор корневой вершины) произвольна и не является свойством MST-дерева. Любое из этих представлений можно преобразовать в любое другое за линейное время.

Выбор представления MST-дерева не оказывает заметного влияния на алгоритм, поскольку каждое из этих представлений можно легко преобразовать в любое другое. Чтобы преобразовать представление MST-дерева в виде графа в вектор ребер, можно воспользоваться функцией GRAPHedges из программы 20.2. Чтобы преобразовать представление в виде родительских ссылок, хранящихся в векторе st (с весами в отдельном векторе wt), в вектор указателей на ребра mst, можно воспользоваться циклом

  for (k = 1; k < G.V(); k++)
    mst[k] = new EDGE (k, st[k], wt[k]);
      

Здесь приведен типичный случай, когда в качестве корня MST-дерева выбирается вершина 0, а фиктивное ребро 0-0 не помещается в список ребер MST-дерева.

Оба эти преобразования тривиальны, но как преобразовать представление в виде вектора указателей на ребра в представление родительскими ссылками? В нашем распоряжении имеются средства, позволяющие легко решить и эту задачу: можно преобразовать представление графа с помощью цикла вроде вышеприведенного (только с вызовом функции insert для каждого ребра), а затем выполнить поиск в глубину из любой вершины, чтобы вычислить за линейное время представление дерева DFS родительскими ссылками.

В общем, хотя представление MST-дерева можно выбирать как удобно, мы оформим все наши алгоритмы в класс обработки графов MST, который вычисляет приватный вектор mst указателей на ребра. В зависимости от потребностей приложений для данного класса можно реализовать функции-члены, которые возвращают этот вектор или предоставляют клиентским программам другую информацию об MST-дереве, но мы не будем вдаваться в дальнейшие детали этого интерфейса. Отметим лишь наличие функции-члена show, которая вызывает аналогичную функцию для каждого ребра MST-дерева (см. упражнение 20.8).

Упражнения

20.8. Напишите класс WeightedEdge (взвешенное ребро), который реализует интерфейс EDGE из программы 20.1 и содержит функцию-член show, которая выводит ребра и их веса в формате, используемом в рисунках этой главы.

20.9. Реализуйте класс io для взвешенных графов, содержащий функции-члены show, scan и scanEZ (см. программу 17.4).

20.10. Постройте АТД графа, который использует целочисленные веса, отслеживает минимальный и максимальный вес в графе и содержит функцию АТД, которая всегда возвращает веса, представленные числами из диапазона от 0 до 1.

20.11. Приведите интерфейс наподобие программы 20.1 для работы клиентов и реализаций с переменными типа Edge (а не с указателями на них).

20.12. Разработайте реализацию интерфейса из упражнения 20.11, в которой используется минимальное представление матрицей весов, а функция итератора nxt использует информацию, неявно содержащуюся в индексах строк и столбцов, для создания переменных типа Edge и возврата его значения клиентской программе.

20.13. Реализуйте класс итератора для использования в программе 20.5 (см. программу 20.4).

20.14. Разработайте реализацию интерфейса из упражнения 20.11, в которой используется минимальное представление списками смежности, узлы списка содержат вес и конечную вершину (но не начальную вершину), а функция итератора nxt использует неявную информацию для создания переменных типа Edge и возврата значений клиентской программе.

20.15. Внесите в генератор разреженных случайных графов из программы 17.12 возможность присваивания ребрам случайных весов (от 0 до 1).

20.16. Внесите в генератор насыщенных случайных графов из программы 17.13 возможность присваивания ребрам случайных весов (от 0 до 1).

20.17. Напишите программу, которая генерирует случайные взвешенные графы, соединяя вершины решетки размером W х W с соседними вершинами (как на рис. 19.3, но для неориентированных графов) и присваивая каждому ребру случайный вес (от 0 до 1).

20.18. Напишите программу генерации случайных полных графов с нормально распределенными весами ребер.

20.19. Напишите программу, которая генерирует V случайных точек на плоскости, затем строит взвешенный граф, соединяя каждую пару точек, расположенных друг от друга на расстоянии не более d, ребрами с весом, равным этому расстоянию (см. упражнение 17.74). Определите, каким должно быть d, чтобы ожидаемое количество ребер было равно E.

20.20. Найдите в интернете крупный взвешенный граф — возможно, карту с расстояниями, список телефонных переговоров с их стоимостями или расписание авиарейсов с ценами на билеты.

20.21. Составьте матрицу размером 8 х 8, содержащую представления родительскими ссылками для всех ориентаций MST-дерева для графа с рис. 20.1. Поместите в i-ю строку этой матрицы представление родительскими ссылками для дерева с корнем в вершине i.

20.22. Предположим, что конструктор класса MST генерирует представление MST-дерева в виде вектора указателей на ребра с элементами от mst[1] до mst[V]. Добавьте функцию-член ST (например, как в программе 18.3) — такую, что ST(v) возвращает в клиентскую программу родителя вершины v в этом дереве (или саму v, если это корень).

20.23. Для условий из упражнения 20.22 напишите функцию-член, которая возвращает суммарный вес MST-дерева.

20.24. Предположим, что конструктор класса MST генерирует представление MST-дерева в виде родительских ссылок в векторе st. Напишите код, который необходимо добавить в конструктор для вычисления представления этого дерева в виде вектора указателей на ребра в элементах приватного вектора mst с индексами 1, ..., V.

20.25. Определите класс TREE (дерево). Затем для условий из упражнения 20.22 напишите функцию-член, которая возвращает результат типа TREE.