|
Здравствуйте прошла курсы на тему Алгоритмы С++. Но не пришел сертификат и не доступен.Где и как можно его скаачат? |
Хеширование
Линейное опробование
Если можно заранее оценить количество элементов, которые должны быть помещены в хеш-таблицу, и имеется достаточно большая непрерывная область памяти, в которой можно поместить все ключи и оставить еще свободные участки, то тогда в хеш-таблице, вероятно, вообще не стоит использовать какие-либо ссылки. Существует несколько методов хранения N элементов в таблице размером M > N, при которых разрешение коллизий основано на использовании пустых мест в таблице. Такие методы называются методами хеширования с открытой адресацией (open-addressing).
Простейший метод открытой адресации называется линейным опробованием (linear probing): при возникновении коллизии (когда хеширование дает адрес в таблице, который уже занят элементом с ключом, не совпадающим с ключом поиска) мы просто проверяем следующую позицию в таблице. Обычно такую проверку (определяющую, содержит ли данная позиция таблицы элемент с ключом, равным ключу поиска) называют пробой (probe). При линейном опробовании определяется один из трех возможных исходов пробы: если позиция таблицы содержит элемент, ключ которого совпадает с искомым, то поиск завершился успешно; в противном случае (если позиция таблицы содержит элемент, ключ которого не совпадает с искомым) мы просто проверяем позицию таблицы с большим индексом, продолжая этот процесс (с возвратом к началу таблицы при достижении ее конца) до тех пор, пока не будет найден искомый ключ или пустая позиция таблицы. Если элемент, содержащий искомый ключ, должен быть вставлен после неудачного поиска, он помещается в пустое место таблицы, где был завершен поиск. Программа 14.4 является реализацией АТД таблицы символов, использующей этот метод. Процесс построения хеш-таблицы с использованием линейного опробования для некоторого набора ключей показан на рис. 14.7.
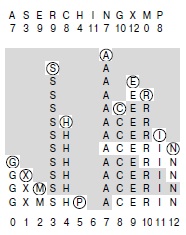
На этой диаграмме показан процесс вставки ключей A S E R C H I N G X M P в первоначально пустую хеш-таблицу с открытой адресацией, размер которой равен 13. Используются показанные вверху хеш-значения и разрешение коллизий методом линейного опробования. Вначале A попадает в позицию 7, затем S попадает в позицию 3, E — в позицию 9. Потом, после коллизии в позиции 9, R попадает в позицию 10 и т.д. При достижении правого конца таблицы опробование продолжается с левого конца: например, последний вставленный ключ P хешируется в позицию 8, но после коллизий в позициях 8—12 и 0—4 попадает в позицию 5. Неопробованные позиции таблицы затенены.
Как и в случае цепочек переполнения, производительность методов с открытой адресацией зависит от коэффициента 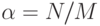 , но при этом он интерпретируется иначе.
, но при этом он интерпретируется иначе.
Программа 14.4. Линейное опробование
Данная реализация таблицы символов хранит элементы в таблице, размер которой вдвое превышает максимально ожидаемое количество элементов и которая первоначально содержит значения nullItem. Таблица содержит сами элементы, но если элементы велики, тип элемента можно изменить, чтобы таблица содержала ссылки на элементы.
Для вставки нового элемента выполняется хеширование в позицию таблицы и ее просмотр вправо (чтобы найти незанятую позицию), используя пустые элементы в незанятых позициях в качестве сигнальных, точно так же, как и при поиске с индексацией по ключам (программа 12.4). Для поиска элемента с данным ключом мы начинаем с хеш-позиции ключа в таблице и просматриваем ее на совпадение, завершая процесс при обнаружении незанятой позиции.
Конструктор устанавливает M таким образом, чтобы таблица была заполнена менее чем наполовину, поэтому, если хеш-функция выдает значения, похожие на случайные, для выполнения остальных операций потребуется всего несколько проб.
private:
Item *st;
int N, M;
Item nullItem;
public:
ST(int maxN)
{ N = 0; M = 2*maxN;
st = new Item[M];
for (int i = 0; i < M; i++) st[i] = nullItem;
}
int count() const
{ return N; }
void insert(Item item)
{ int i = hash(item.key(), M);
while (!st[i].null()) i = (i+1) % M;
st[i] = item; N++;
}
Item search(Key v)
{ int i = hash(v, M);
while (!st[i].null())
if (v == st[i].key())
return st[i];
else
i = (i+1) % M;
return nullItem;
}
В случае цепочек переполнения — среднее количество элементов в одном списке, обычно большее 1. В случае открытой адресации а — доля занятых позиций таблицы; она должна быть меньше 1. Иногда а называют коэффициентом загрузки хеш-таблицы.
В случае разреженной таблицы (значение  мало) очевидно, что для большинства операций поиска пустая позиция будет найдена после всего нескольких проб. В случае почти полной таблицы (значение близко
мало) очевидно, что для большинства операций поиска пустая позиция будет найдена после всего нескольких проб. В случае почти полной таблицы (значение близко  к 1) для выполнения поиска может потребоваться очень большое количество проб, а при полностью заполненной таблице поиск может даже привести к бесконечному циклу. Как правило, чтобы время поиска не было слишком большим, при использовании линейного опробования нужно не допускать заполнения таблицы. То есть вместо того, чтобы использовать дополнительную память для ссылок, она используется для создания дополнительного места в хеш-таблице, что позволяет сократить последовательности проб. При использовании линейного опробования размер таблицы больше, чем с цепочками переполнения, т.к. необходимо соблюдение условия M > N, но общий объем используемой памяти может быть меньше, поскольку не используются ссылки. Вопросы сравнения используемого объема памяти будут подробно рассмотрены в разделе 14.5; а пока проанализируем время выполнения линейного опробования как функцию от
к 1) для выполнения поиска может потребоваться очень большое количество проб, а при полностью заполненной таблице поиск может даже привести к бесконечному циклу. Как правило, чтобы время поиска не было слишком большим, при использовании линейного опробования нужно не допускать заполнения таблицы. То есть вместо того, чтобы использовать дополнительную память для ссылок, она используется для создания дополнительного места в хеш-таблице, что позволяет сократить последовательности проб. При использовании линейного опробования размер таблицы больше, чем с цепочками переполнения, т.к. необходимо соблюдение условия M > N, но общий объем используемой памяти может быть меньше, поскольку не используются ссылки. Вопросы сравнения используемого объема памяти будут подробно рассмотрены в разделе 14.5; а пока проанализируем время выполнения линейного опробования как функцию от  .
.
Средние затраты на выполнение линейного опробования зависят от того, как элементы при их вставке объединяются в непрерывные группы занятых ячеек таблицы, называемые кластерами (cluster). Рассмотрим следующие два крайних случая заполненной наполовину (M = 2N) таблицы линейного опробования. В лучшем случае позиции таблицы с четными индексами будут пустыми, а с нечетными — занятыми (или наоборот — прим. перев.). В худшем случае первая (вообще-то любая непрерывная — прим. перев.) половина позиций таблицы будет пустой, а вторая — заполненной. Средняя длина кластеров в обоих случаях равна N/(2N) = 1/2, но среднее количество проб при неудачном поиске равно 1 (нужна по меньшей мере одна проба) плюс
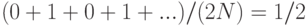
в лучшем случае и 1 плюс
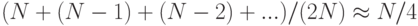
в худшем случае.
Обобщая эти рассуждения, приходим к выводу, что среднее количество проб при неудачном поиске пропорционально квадратам длин кластеров. Среднее значение рассчитывается путем вычисления затрат при неудачном поиске, начиная с каждой позиции таблицы, и деления суммы на M. Для неудачного поиска требуется не менее 1 пробы, поэтому будем считать количество проб, следующих за первой. Если кластер имеет дину t, то вклад этого кластера в общую сумму определяется выражением
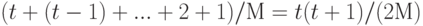
Сумма длин кластеров равна N, поэтому, суммируя эти затраты для всех ячеек в таблице, находим, что общие средние затраты при неудачном поиске равны 1 + N / (2M) плюс сумма квадратов длин кластеров, деленная на 2M. Имея заданную таблицу, можно быстро вычислить средние затраты на неудачный поиск в этой таблице (см. упражнение 14.28), но общую аналитическую формулу дать трудно, поскольку кластеры образуются в результате сложного динамического процесса (алгоритма линейного опробования).
Лемма 14.3. При разрешении коллизий с помощью линейного опробования среднее количество проб, нужных для поиска в хеш-таблице размером M, которая содержит 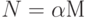 ключей, приблизительно равно
ключей, приблизительно равно
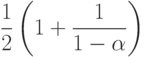 и
и
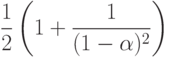
соответственно для успешного и неудачного поиска.
Несмотря на сравнительно простую форму этих результатов, точный анализ линейного опробования представляет собой сложную задачу. Его вывод, полученный Кнутом (Knuth) в 1962 г., явился значительной вехой в анализе алгоритмов (см. раздел ссылок). 
Точность этих выражений уменьшается с приближением значения  к 1, но в данном случае это не важно, поскольку в любом случае линейное опробование не следует использовать в почти заполненной таблице. Для меньших значений а равенства достаточно точны. Ниже приведена таблица, в которую сведены ожидаемые количества проб при успешном и неудачном поиске с использованием линейного опробования:
к 1, но в данном случае это не важно, поскольку в любом случае линейное опробование не следует использовать в почти заполненной таблице. Для меньших значений а равенства достаточно точны. Ниже приведена таблица, в которую сведены ожидаемые количества проб при успешном и неудачном поиске с использованием линейного опробования:
коэффициент загрузки ( ) )
|
1/2 | 2/3 | 3/4 | 9/10 |
|---|---|---|---|---|
| успешный поиск | 1,5 | 2,0 | 3,0 | 5,5 |
| неудачный поиск | 2,5 | 5,0 | 8,5 | 55,5 |
Для неудачного поиска всегда требуются большие затраты, чем для успешного, и можно ожидать, что в обоих случаях в заполненной менее чем наполовину таблице в среднем требуется лишь несколько проб.
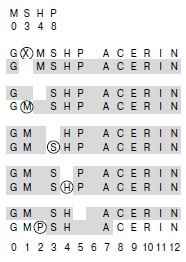
На этой диаграмме показан процесс удаления ключа X из таблицы, показанной на рис. 14.7. Во второй строке показан результат простого удаления X из таблицы, что неприемлемо, поскольку в этом случае M и P оказываются отрезаны от своиххеш-позиций пустой позицией, оставшейся после X. Поэтому ключи M, S, H и P (справа от X в этом же кластере) повторно вставляются в указанном порядке с использованием хеш-значений, указанных сверху, и с разрешением коллизий с помощьюли-нейного опробования. M заполняет свободное место, оставленное ключом X, потом в таблицу без коллизий вставляются S и H, а затем в позицию 2 вставляется P.
Как и в случае цепочек переполнения, выбор, хранить ли в таблице элементы с повторяющимися ключами, предоставляется клиенту. Такие элементы не обязательно размещаются в таблице с линейным опробованием в соседних позициях — среди элементов с одинаковыми ключами могут размещаться и другие элементы с таким же хеш-значением.
По самой сути построения ключи в таблице, построенной с помощью линейного опробования, размещаются в случайном порядке. В результате операции АТД сортировать и выбрать требуют выполнения заново по одному из методов, описанных в лекциях 6-10. Поэтому линейное опробование не годится для приложений, в которых эти операции выполняются часто.
А как удалить ключ из таблицы, построенной с помощью линейного опробования? Просто убрать его нельзя, поскольку элементы, которые были вставлены позже, могли перескочить через этот элемент, и поэтому их поиск будет постоянно прерываться на пустой позиции, оставшейся после удаленного элемента. Одно из решений этой проблемы заключается в повторном хешировании всех элементов, для которых эта проблема могла бы возникнуть — между удаленным элементом и следующей незанятой позицией справа от него. Пример, иллюстрирующий этой процесс, приведен на рис. 14.8, а программа 14.5 содержит реализацию этого подхода. В разреженной таблице в большинстве случаев такой процесс потребует лишь нескольких операций повторного хеширования. Другой способ реализации удаления — замена удаленного ключа сигнальным ключом, который будет служить заполнителем для поиска, но может быть повторно использован для вставок (см. упражнение 14.33).
Программа 14.5. Удаление из хеш-таблицы с линейным опробованием
Для удаления элемента с заданным ключом выполняется поиск этого элемента и замена его пустым элементом nullItem. Затем необходимо внести изменения на случай, если какой-либо элемент, расположенный справа от теперь незанятой позиции, хешируется в эту позицию или левее нее, т.к. свободная позиция может привести к прерыванию поиска такого элемента. Поэтому выполняется повторная вставка всех элементов, расположенных в одном кластере с удаленным элементом правее него. Поскольку таблица заполнена менее чем наполовину, в среднем количество повторно вставляемых элементов будет мало.
void remove(Item x)
{ int i = hash(x.key(), M), j;
while (!st[i].null())
if (x.key() == st[i].key())
break;
else
i = (i+1) % M;
if (st[i].null()) return;
st[i] = nullItem; N--;
for (j = i+1; !st[j].null(); j = (j + 1) % M, N--)
{ Item v = st[j]; st[j] = nullItem; insert(v); }
}
Упражнения
14.24. Какое время может потребоваться в худшем случае для вставки N ключей в первоначально пустую таблицу при использовании линейного опробования?
14.25. Приведите содержимое хеш-таблицы, образованной вставками элементов с ключами E A S Y Q U T I O N в указанном порядке в первоначально пустую таблицу размером M= 16, использующую линейное опробование. Для преобразования k-ой буквы алфавита в индекс таблицы используйте хеш-функцию 11k mod М.
14.26. Выполните упражнение 14.25 для М = 10.
14.27. Напишите программу, которая вставляет 105 случайных неотрицательных целых чисел, меньших 106, в таблицу размером 105, использующую линейное опробование. Программа должна выводить гистограмму количества проб, использованных для каждых 103 последовательных вставок.
14.28. Напишите программу, которая вставляет N/2случайных целых чисел в таблицу размером N, использующую линейное опробование, а затем на основании длин кластеров вычисляет средние затраты на неудачный поиск в результирующей таблице, для N= 103, 104, 105 и 106 .
14.29. Напишите программу, которая вставляет N/2случайных целых чисел в таблицу размером N, использующую линейное опробование, а затем вычисляет средние затраты на успешный поиск в результирующей таблице, для N= 103, 104, 105 и 106 . Не выполняйте поиск всех ключей после построения таблицы (отслеживайте затраты на ее построение).
14.30. Определите экспериментальным путем, изменяются ли средние затраты на успешный и неудачный поиск в случае выполнения длинной последовательности чередующихся случайных вставок и удалений с помощью программ 14.4 и 14.5 в хеш-таблице размером 2N, содержащей N ключей, для N = 10, 100 и 1000 и до N2 пар вставок-удалений для каждого значения N.